2.5 Newton’s Third Law and Free-Body Diagrams: Understanding Force Interactions
Force Vectors ➡️
Force vectors are quantities that possess both magnitude and direction, making them vector quantities. Examples of vector quantities in physics include force, displacement, velocity, and acceleration. These are often represented visually with arrows, where the length of the arrow corresponds to the magnitude, and the arrow’s direction indicates the vector’s direction.

Key Vocabulary
- Vector: Quantities that have both size (magnitude) and direction (e.g., “The ball moves 5 meters to the east”).
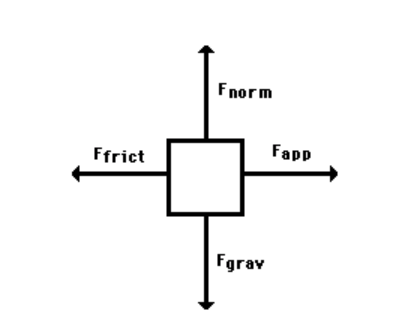
- Free-Body Diagram: A visual tool used to show all external forces acting on a body. In these diagrams, the body is represented by a simple shape (often a dot or box), and all forces are depicted as arrows pointing in the direction they act.
Constructing Free-Body Diagrams
When drawing free-body diagrams, there are several important forces to remember:
- Force of Gravity (Weight): Always points downwards, directed towards the Earth’s center.
- Normal Force: Acts perpendicular to the contact surface and opposes gravity.
- Frictional Force: Opposes the direction of motion or attempted motion.
- Applied Force: Points in the direction of the force applied.
- Tension: Acts along ropes, strings, or chains and pulls along their length.
Example: Imagine a box being pushed across a floor with a force of 50 N to the right while a frictional force of 30 N acts to the left.
- Diagram Representation: Include arrows for applied force, frictional force, and gravitational and normal forces acting on the box.
Calculating Resultant Forces
To find the net force acting on an object, sum up all individual force vectors:
Example Calculation
A 10 kg box is pushed to the right with a force of 50 N while friction provides a 30 N force to the left. Calculate the acceleration using Newton’s Second Law (F=ma).
- Net Force:
- Acceleration:
Force Interactions 🛠
Forces always result from interactions between objects. For example:
- When you push against a wall, the wall exerts an equal and opposite force on you.
- When you clap your hands, each hand exerts a force on the other.
Newton’s Third Law of Motion: Action-Reaction Pairs 🤝
Newton’s Third Law states:
“For every action, there is an equal and opposite reaction.”
This means that whenever one object exerts a force on another, the second object exerts an equal and opposite force on the first object. These action-reaction pairs occur in every interaction.
Key Vocabulary
- Action-Reaction Pair: The interaction between two objects where one object exerts a force on the other, and the second object exerts a force back with equal magnitude but in the opposite direction.
Practical Examples of Action-Reaction Pairs
- Pushing Against a Wall: When you push against a wall, it pushes back on you with an equal and opposite force.
- Gravity: The Earth pulls on an object with a gravitational force, and the object pulls back on the Earth with an equal and opposite force.
- Normal Force: When an object rests on a surface, the surface pushes back with a normal force equal to the weight of the object.
- Tension: A stretched rope exerts equal and opposite forces on the objects at each end.
- Friction: As an object slides across a surface, friction acts to resist motion, and the object exerts an equal force in the opposite direction.
Using Free-Body Diagrams for Problem Solving
Example Problem
Scenario: A 4 kg block slides down a ramp inclined at 30° with a coefficient of friction of 0.4.
Solution:
- Gravitational Force:
- Normal Force:
- Frictional Force:
- Parallel Component of Gravity:
- Net Force:
- Acceleration:
Key Takeaways
- Forces are vector quantities with magnitude and direction.
- Free-body diagrams are invaluable for visualizing forces acting on a system.
- Newton’s Third Law emphasizes that forces come in pairs—action and reaction forces are always equal in magnitude and opposite in direction.