Have you ever been stumped by the challenge of solving a triangle that doesn’t have a right angle? The mysterious “cosine law” might just be the key you’ve been searching for. Whether you’re a student wrestling with trigonometry or a professional in engineering, navigation, or physics, the cosine law unlocks the secrets of non‐right-angled triangles, enabling you to compute unknown sides and angles with precision.
Introduction
The cosine law—often known as the law of cosines or the cosine rule—is a fundamental theorem in trigonometry that bridges the gap between algebra and geometry. In this comprehensive guide, we will explore every aspect of the cosine law: from its clear definition and elegant derivation to its fascinating historical roots and wide-ranging modern applications.
Imagine being able to accurately determine the distance between two points on a map, even when the connecting path doesn’t form a perfect right angle. This capability is one of the many reasons why understanding the cosine law is so powerful. In the sections that follow, you’ll discover a straightforward definition, a detailed derivation using geometric and analytic methods, real-world examples from navigation and engineering, common misconceptions clarified, and insights into the modern relevance of the cosine law. Whether you’re just beginning your trigonometric journey or looking to deepen your understanding, this post has something for everyone.
What is the Cosine Law?
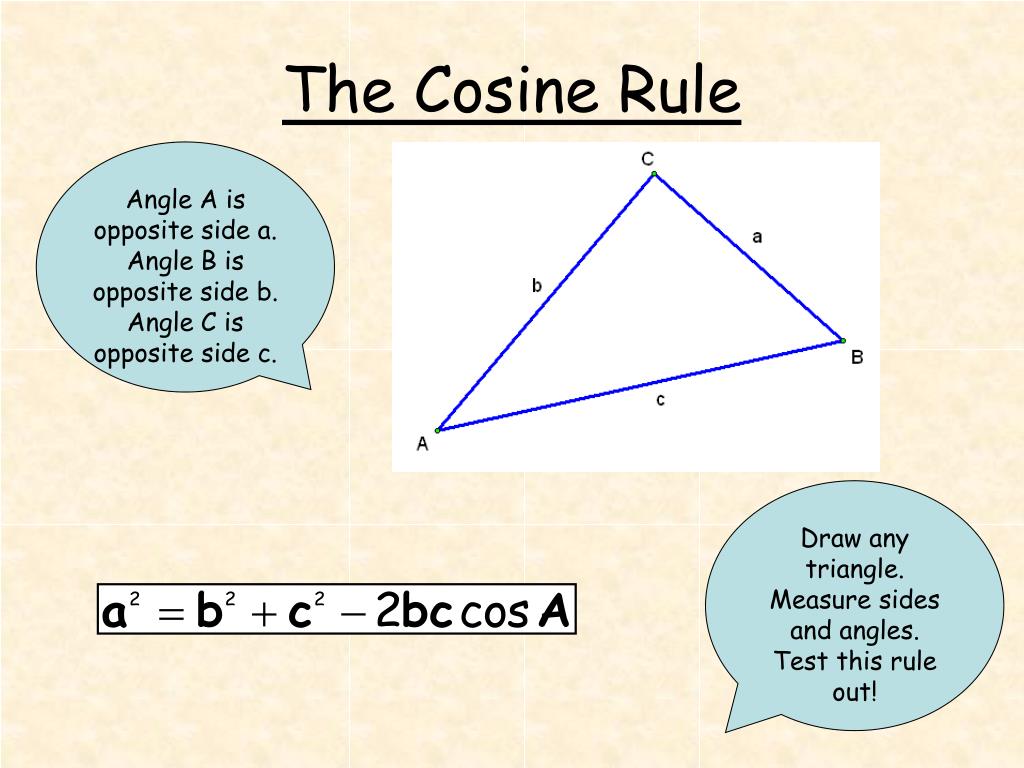
The cosine law is an equation that relates the lengths of the sides of any triangle to the cosine of one of its angles. It generalizes the well-known Pythagorean theorem by extending its applicability from right-angled triangles to any arbitrary triangle. For a triangle with sides \(a\), \(b\), and \(c\) (where \(c\) is opposite angle \(C\)), the cosine law is expressed as:
$$ c^2 = a^2 + b^2 - 2ab\cos(C) $$
Similarly, by cyclic permutation, the formula can be written for the other sides:
- $$ a^2 = b^2 + c^2 - 2bc\cos(A) $$
- $$ b^2 = a^2 + c^2 - 2ac\cos(B) $$
This powerful equation enables you to determine an unknown side or angle when you have sufficient information about the triangle. Whether you are given two sides and the included angle or all three sides, the cosine law is an indispensable tool for solving triangles.
Historical and Contextual Background
The origins of the cosine law date back to ancient civilizations that sought to understand the world around them through geometry and astronomy. Early Greek mathematicians such as Euclid and Ptolemy laid the groundwork for trigonometry, and the ideas underlying the cosine law evolved over centuries. Although the formal statement of the cosine law was refined by later scholars, its intuitive basis can be seen in the work of these ancient pioneers.
During the Middle Ages, Islamic mathematicians further advanced trigonometric concepts, improving the precision of astronomical observations and geometric calculations. Their contributions helped bridge the gap between ancient Greek geometry and the algebraic methods of the Renaissance. Today, the cosine law is a testament to the cumulative nature of mathematical discovery, reflecting centuries of intellectual evolution.
The cosine law has since become a cornerstone in various fields—including navigation, surveying, physics, and computer graphics—demonstrating its timeless relevance and versatility.
Derivation and Mathematical Exploration
One of the most intriguing aspects of the cosine law is its derivation. Although the formula appears elegantly simple, arriving at it requires a blend of geometric insight and algebraic manipulation. Below are two common methods of deriving the cosine law.
Geometric Derivation
Consider a triangle with vertices \(A\), \(B\), and \(C\). Drop a perpendicular from vertex \(C\) to the line containing side \(AB\) (let this foot be \(D\)). By decomposing the triangle into two right-angled triangles, you can apply the Pythagorean theorem to each.
Denote the length of segment \(AD\) as \(x\) and let the altitude from \(C\) be \(h\). The lengths of the sides can be related to \(x\) and \(h\) via trigonometric functions. After expressing \(x\) in terms of \(\cos(C)\) and simplifying the resulting equations, you eventually arrive at the cosine law:
$$ c^2 = a^2 + b^2 - 2ab\cos(C) $$
Notice that when the angle \(C\) is \(90^\circ\), since \(\cos(90^\circ) = 0\), the formula reduces to the familiar Pythagorean theorem:
$$ c^2 = a^2 + b^2 $$
Analytic Approach Using Vectors
Another elegant derivation of the cosine law utilizes vector algebra. Suppose you have two vectors \(\mathbf{a}\) and \(\mathbf{b}\) with an angle \(C\) between them. The square of the magnitude of the difference \(\|\mathbf{a} - \mathbf{b}\|^2\) is given by:
$$ \|\mathbf{a} - \mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2 - 2\|\mathbf{a}\|\|\mathbf{b}\|\cos(C) $$
Recognizing that \(\|\mathbf{a} - \mathbf{b}\|\) corresponds to the length of the side opposite angle \(C\) in a triangle, we recover the cosine law:
$$ c^2 = a^2 + b^2 - 2ab\cos(C) $$
This method not only reinforces the connection between geometry and algebra but also underscores the broad applicability of the cosine law across different mathematical frameworks.
Applications and Real-World Examples
The cosine law is far more than an abstract mathematical concept—it has numerous practical applications that impact our everyday lives. Below are some detailed examples of how the cosine law is used in various fields.
Navigation and Surveying
In navigation and land surveying, accurate distance measurements are crucial. When direct measurement is impractical—especially in oblique or irregular terrain—the cosine law allows surveyors to determine distances between points with high precision. For instance, when mapping property boundaries or planning infrastructure projects, surveyors use the cosine law to calculate unknown distances and angles, even when the triangle formed by the points is not right-angled.
Similarly, in marine and aerial navigation, determining the course and distance between two locations often involves solving oblique triangles. By applying the cosine law, navigators can accurately compute the distance between landmarks, ensuring safe and efficient travel.
Engineering and Architecture
Engineers and architects frequently encounter non‐right-angled triangles when designing structures such as bridges, buildings, and roadways. The cosine law is indispensable in these scenarios. For example, when designing a truss bridge, the forces acting on each component must be precisely calculated. The cosine law is used to determine the resultant forces on the angled members, ensuring that the structure can withstand various loads.
In architectural design, the cosine law helps in the planning and layout of irregularly shaped structures. By accurately determining side lengths and angles, architects can ensure that their designs are both aesthetically pleasing and structurally sound.
Astronomy and Space Science
Astronomers have long relied on trigonometric principles to measure the vast distances between celestial bodies. When the positions of stars or planets do not form right angles, the cosine law becomes essential. By applying the cosine law, astronomers can calculate the distances between stars, planets, and other celestial objects with remarkable accuracy.
In astrodynamics, understanding the spatial relationships between objects in space is critical for planning satellite trajectories and space missions. The cosine law provides the mathematical foundation for these calculations, making it a vital tool in modern astronomy and space science.
Importance, Applications, and Benefits
The significance of the cosine law extends beyond academic theory. Here are some key reasons why mastering the cosine law is beneficial:
- Simplification of Complex Problems: The cosine law transforms complex geometric problems into manageable algebraic equations, allowing for the straightforward solution of triangles that are not right-angled.
- Versatility Across Disciplines: From navigation and surveying to engineering and astronomy, the cosine law is used in a wide array of fields. Its broad applicability makes it an essential tool for many professionals.
- Foundation for Advanced Mathematics: A solid grasp of the cosine law paves the way for deeper exploration into topics such as vector calculus, computational geometry, and even computer graphics.
- Enhanced Problem-Solving Skills: Learning to apply the cosine law improves analytical and logical reasoning, skills that are valuable both in and out of the classroom.
Common Misconceptions and FAQs
Despite its widespread use, several misconceptions about the cosine law still exist. Let’s address some of these common misunderstandings:
-
Misconception 1: The Cosine Law Only Applies to Oblique Triangles
While the cosine law is particularly useful for non‐right-angled triangles, it is a general theorem that holds true for all triangles. In the special case where the triangle is right-angled, the cosine law simplifies to the Pythagorean theorem.
-
Misconception 2: The Cosine Law is the Same as the Sine Law
Although both laws are used to solve triangles, they are applicable in different scenarios. The sine law is most effective when dealing with angles and their opposite sides, whereas the cosine law is ideal when two sides and the included angle, or all three sides, are known.
-
Misconception 3: The Cosine Law is Too Complex for Practical Use
In reality, once you understand the derivation and the relationships involved, the cosine law is straightforward to apply. With practice, solving problems using this law becomes an intuitive process.
Frequently Asked Questions (FAQs)
Q1: What is the primary difference between the cosine law and the Pythagorean theorem?
The Pythagorean theorem is a special case of the cosine law that applies only to right-angled triangles. In contrast, the cosine law can be used for any triangle. When the angle is \(90^\circ\), \(\cos(90^\circ) = 0\) and the cosine law reduces to the Pythagorean theorem.
Q2: Can the cosine law be used to find an angle if all three sides are known?
Yes. If you know all three sides of a triangle, you can rearrange the cosine law to solve for an angle. For example, to find angle \(C\), you can use:
$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2ab} $$
Q3: Is the cosine law applicable to three-dimensional problems?
The cosine law is primarily used for planar triangles. However, its underlying principles can be extended to solve certain three-dimensional problems, particularly when dealing with oblique components and angles.
Modern Relevance and Current Trends
In today’s fast-paced technological world, the principles of the cosine law continue to find new applications. Modern fields such as computer graphics, robotics, and artificial intelligence rely on trigonometric methods to solve complex spatial problems.
For example, in computer graphics, the cosine law helps calculate lighting angles, shading, and realistic rendering of 3D objects. In robotics, it is used to determine the precise movement of robotic arms and navigation paths for autonomous vehicles. As technology advances, the integration of classical trigonometric principles with modern computational algorithms further emphasizes the enduring importance of the cosine law.
Additionally, research in data analytics and machine learning often involves spatial analysis in multidimensional spaces, where the cosine law is applied to measure similarities and distances. These modern applications showcase how an ancient mathematical discovery continues to influence cutting-edge technologies.
Detailed Derivation Using Coordinate Geometry
Another intuitive approach to derive the cosine law is by employing coordinate geometry. Imagine placing one vertex of a triangle at the origin of a Cartesian coordinate system and aligning one of its sides along the positive x-axis. For example, let vertex \(A\) be at \((0, 0)\), vertex \(B\) at \((b, 0)\), and vertex \(C\) at some point \((x, y)\).
In this setup, the side lengths can be expressed in terms of coordinates:
- The distance \(c\) (between \(A\) and \(C\)) is given by: $$ c = \sqrt{x^2 + y^2} $$
- The distance \(a\) (between \(B\) and \(C\)) is: $$ a = \sqrt{(x-b)^2 + y^2} $$
By computing the dot product of the vectors representing the sides and applying the definition of cosine for the angle at \(A\) or \(B\), you can rearrange the expressions to reveal the cosine law. This derivation using coordinate geometry underscores the interplay between algebra and geometry, highlighting the robustness of the cosine law.
Spherical Trigonometry and the Cosine Law
When dealing with curved surfaces such as the Earth or celestial spheres, the cosine law must be adapted to spherical geometry. In spherical trigonometry, the cosine law is modified to work with angular distances (measured in radians) along the surface of a sphere. The spherical cosine law is expressed as:
$$ \cos(c) = \cos(a)\cos(b) + \sin(a)\sin(b)\cos(C) $$
In this formula, \(a\), \(b\), and \(c\) represent the angular distances between points on the sphere, and \(C\) is the angle opposite side \(c\). This formulation is essential in fields such as astronomy, geodesy, and global navigation satellite systems (GNSS), where it is used to accurately compute distances and angles on curved surfaces.
Cosine Law in Robotics and Computer Vision
Modern robotics and computer vision rely on precise mathematical models to interact with the environment. The cosine law plays a critical role in these fields. For example, the segments of a robotic arm often form triangles. By applying the cosine law, engineers can determine the exact angles each joint must achieve to position the end-effector at a desired location.
In computer vision, the cosine law assists in reconstructing three-dimensional scenes from two-dimensional images. Techniques like stereo vision use the cosine law to determine the depth and relative positions of objects, enabling technologies such as autonomous navigation and augmented reality.
Exercises and Practice Problems
To solidify your understanding of the cosine law, try working through the following exercises:
Exercise 1: Solving for a Side
Given a triangle with sides \(a = 5\) units, \(b = 8\) units, and an included angle \(C = 45^\circ\), find the length of side \(c\).
Use the cosine law:
$$ c^2 = a^2 + b^2 - 2ab\cos(45^\circ) $$
Substitute the values and solve for \(c\).
Exercise 2: Finding an Angle
In a triangle, the sides are \(a = 9\) units, \(b = 10\) units, and \(c = 7\) units. Determine the measure of angle \(C\) opposite side \(c\).
Rearranging the cosine law:
$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2ab} $$
Calculate \(\cos(C)\) and then use the inverse cosine function to find \(C\).
Exercise 3: Application in Navigation
A surveyor measures distances of 120 meters and 150 meters from a fixed point to two landmarks with an included angle of \(70^\circ\). Calculate the distance between the two landmarks.
Apply the cosine law:
$$ c^2 = 120^2 + 150^2 - 2(120)(150)\cos(70^\circ) $$
After computing \(c^2\), take the square root to find \(c\).
Common Pitfalls and How to Avoid Them
When applying the cosine law, be mindful of these common pitfalls:
- Incorrect Angle Identification: Always verify that the angle you use is opposite the side you wish to compute.
- Misapplying the Formula: Ensure that you correctly identify which sides and angle are known. Double-check your triangle’s configuration before substituting values.
- Rounding Errors: When calculating trigonometric functions, maintain as many decimal places as possible during intermediate steps and only round your final answer.
- Confusing Trigonometric Laws: Remember that the sine law and cosine law are used in different contexts. Use the sine law when dealing with ratios of sides to angles, and the cosine law when two sides and the included angle (or three sides) are known.
Teaching Strategies for the Cosine Law
For educators, presenting the cosine law in an engaging manner can make all the difference. Consider these strategies:
- Interactive Demonstrations: Use dynamic geometry software such as GeoGebra to allow students to visually manipulate triangles and observe how changes in angles and sides affect the cosine law.
- Real-World Examples: Integrate applications from navigation, engineering, and astronomy to illustrate the law’s practical relevance.
- Group Activities: Encourage collaborative problem-solving sessions where students work together on challenging triangle problems.
- Step-by-Step Explanations: Break down the derivation and application into clear, manageable steps, reinforcing learning with plenty of practice problems.
- Technology Integration: Use online tools and mobile apps to provide interactive and engaging learning experiences.
Further Reading and Research Opportunities
For those eager to delve deeper into the world of trigonometry, consider exploring these topics:
- Advanced Trigonometric Identities: Study how the cosine law interacts with other identities to solve complex problems.
- Spherical and Hyperbolic Geometry: Investigate adaptations of the cosine law in non-Euclidean geometries, relevant in astronomy and cosmology.
- Computational Methods: Learn how modern algorithms and simulation tools integrate the cosine law for real-time calculations.
- Historical Evolution: Research the development of trigonometric principles from ancient Greek and Islamic scholars to modern mathematics.
The Ambiguous Case in Triangle Solving
In some situations—particularly when using the sine law—you may encounter the ambiguous case (or SSA condition), where two different triangles satisfy the given conditions. While the cosine law avoids this ambiguity when two sides and the included angle are known, understanding the differences between these approaches is important for solving triangle problems accurately.
Recognizing that the cosine law provides a unique solution in cases where the triangle is fully determined helps build confidence in your calculations.
Implications in Advanced Physics and Engineering
The cosine law is not just a classroom tool; it plays a significant role in advanced fields such as physics and engineering. In mechanics, for instance, resolving forces that act at various angles is essential. The cosine law allows engineers to accurately compute the net force on an object by considering the contribution of each vector component.
In electromagnetism and aerospace engineering, the cosine law is used to calculate resultant fields and trajectory adjustments, respectively. Its applications in these high-stakes domains underscore the importance of mastering this essential trigonometric tool.
Integrating the Cosine Law into Everyday Problem Solving
Beyond academic and professional applications, the cosine law can help solve everyday problems. Whether you’re planning a DIY project, designing a garden, or mapping out the layout of your home, understanding the relationships between sides and angles can lead to more precise and effective solutions.
For instance, when designing a triangular garden bed or a custom piece of furniture, applying the cosine law ensures that the dimensions are correct and the angles are precisely measured. This practical application shows that the cosine law isn’t just for experts—it’s a versatile tool for anyone who enjoys problem solving.
Real-Life Testimonials: How the Cosine Law Has Made a Difference
Many professionals have found that a solid understanding of the cosine law has significantly improved their work. Here are a few testimonials:
"As an engineer working on bridge design, I rely on the cosine law daily. It has streamlined my calculations and helped ensure that my structures are safe and efficient." — Alex M., Structural Engineer
"During my research in astronomy, the cosine law was crucial in mapping the positions of stars. It provided a solid foundation for my studies and opened up new avenues for celestial navigation." — Dr. Linda H., Astronomer
"I never imagined a math formula could be so practical. Whether I'm planning a home project or working on a technical problem at work, the cosine law is always a reliable tool." — Jamie L., Hobbyist
Exploring the Cosine Law Through Interactive Media
Interactive media offers innovative ways to grasp the concepts behind the cosine law. Online platforms like GeoGebra and Desmos allow users to experiment with triangle configurations in real time. By adjusting side lengths and angles interactively, you can see firsthand how the cosine law applies, making abstract concepts tangible and engaging.
Historical Anecdotes and the Evolution of Trigonometry
The story of the cosine law is intertwined with the rich history of trigonometry. Ancient Greek mathematicians, including Euclid and Ptolemy, laid the initial groundwork with their studies of geometry. Centuries later, scholars during the Islamic Golden Age—such as Al-Battani and Al-Kashi—refined these ideas, contributing to the precise formulations used today.
This historical evolution not only highlights the cumulative nature of mathematical discovery but also demonstrates how ancient principles continue to influence modern science and technology. The cosine law is a living legacy of human curiosity and ingenuity.
In Summary: The Enduring Value of the Cosine Law
Throughout this extensive guide, we have explored the cosine law from multiple angles—its definition, derivation, historical context, real-world applications, and common pitfalls. The cosine law is much more than just a formula; it is a powerful tool that transforms complex geometric problems into solvable equations, enriching our understanding of both the natural and engineered worlds.
Whether you are a student, educator, or professional, mastering the cosine law enhances your problem-solving abilities and opens up new perspectives on how mathematics underpins everyday phenomena. It is a timeless piece of mathematical wisdom that continues to inspire and enable innovation.
Call to Action
Now that you have gained an in-depth understanding of the “cosine law,” it’s time to put your knowledge into practice. Explore additional problems, experiment with interactive tools, and share your insights with peers. Whether you’re tackling complex engineering designs or simply satisfying your curiosity, the cosine law is a tool that will serve you well.
If you found this guide helpful, please share it with others, leave a comment below, or subscribe to our blog for more insightful articles on mathematics and its applications. Your feedback and engagement are invaluable in building a community of lifelong learners who appreciate the beauty and practicality of mathematics.
Final Thoughts
The journey through the cosine law illustrates how ancient mathematical insights continue to shape our modern world. Whether applied in navigation, engineering, astronomy, or everyday problem solving, the cosine law remains a vital tool that encapsulates the elegance and utility of mathematics.
Embrace the challenge, experiment with its applications, and let the cosine law transform the way you approach complex problems. Every new problem solved deepens your appreciation for the interconnectedness of mathematical concepts and their real-world implications.
Thank you for reading this comprehensive guide on the “cosine law.” We hope it has enriched your understanding and inspired you to explore further. Happy calculating!