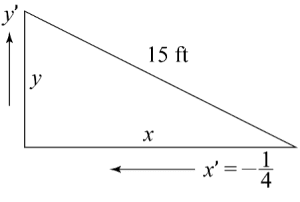About Us Donate

Algebra Cheat Sheet Basic Properties & Facts

Algebra Cheat Sheet Basic Properties & Facts

Table of Contents

Algebra Cheat Sheet, Basic Properties & Facts

Properties of Radicals

  • an=a1/n\sqrt[n]{a} = a^{1/n}   
  • abn=an⋅bn\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b} 
  • anm=amn\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} 
  • abn=anbn\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} 
  • ann=a\sqrt[n]{a^n} = a  (if nnis odd)
  • ann=∣a∣\sqrt[n]{a^n} = |a|  (if nnis even)

Properties of Inequalities

  • If a<ba < b  , then:
    • a+c<b+ca + c < b + c  and a−c<b−ca – c < b – c 
  • If a<ba < b  and c>0c > 0, then:
    • ac<bcac < bc  and ac<bc\frac{a}{c} < \frac{b}{c}
  • If a<ba < b  and c<0c < 0, then:
    • ac>bcac > bc  and ac>bc\frac{a}{c} > \frac{b}{c}

Properties of Absolute Value

  • ∣a∣={aif a≥0−aif a<0|a| = \begin{cases} a & \text{if } a \geq 0 \\ -a & \text{if } a < 0 \end{cases} 
  • ∣a∣≥0|a| \geq 0   
  • ∣−a∣=∣a∣|-a| = |a|   
  • ∣ab∣=∣a∣⋅∣b∣|ab| = |a| \cdot |b|   
  • ∣ab∣=∣a∣∣b∣\left| \frac{a}{b} \right| = \frac{|a|}{|b|}  (provided b≠0b \neq 0)
  • ∣a+b∣≤∣a∣+∣b∣|a + b| \leq |a| + |b|  (Triangle Inequality)

Distance Formula

If P1=(x1,y1)P_1 = (x_1, y_1)  and P2=(x2,y2)P_2 = (x_2, y_2)  are two points, the distance between them is given by:

d(P1,P2)=(x2−x1)2+(y2−y1)2d(P_1, P_2) = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}

Complex Numbers

  • i=−1i = \sqrt{-1}
  • i2=−1i^2 = -1 
  • −a=ia\sqrt{-a} = i\sqrt{a}, where a≥0a \geq 0 

Operations with Complex Numbers

  1. Addition: (a+bi)+(c+di)=(a+c)+(b+d)i(a + bi) + (c + di) = (a + c) + (b + d)i 
  2. Subtraction: (a+bi)−(c+di)=(a−c)+(b−d)i(a + bi) – (c + di) = (a – c) + (b – d)i 
  3. Multiplication: (a+bi)(c+di)=(ac−bd)+(ad+bc)i(a + bi)(c + di) = (ac – bd) + (ad + bc)i 
  4. Multiplication with Conjugates: (a+bi)(a−bi)=a2+b2(a + bi)(a – bi) = a^2 + b^2 

Complex Modulus

∣a+bi∣=a2+b2|a + bi| = \sqrt{a^2 + b^2}

Complex Conjugate

The conjugate of (a+bi)(a + bi)  is denoted by:

(a+bi)‾=a−bi\overline{(a + bi)} = a – bi 

Relation Between Modulus and Conjugate

(a+bi)‾⋅(a+bi)=∣a+bi∣2\overline{(a + bi)} \cdot (a + bi) = |a + bi|^2 

Logarithms and Log Properties

Definition

If y=log⁡bxy = \log_b x , it is equivalent to x=byx = b^y .

Example

log⁡5125=3because53=125\log_5 125 = 3 \quad \text{because} \quad 5^3 = 125 

Special Logarithms

  • ln⁡x=log⁡ex\ln x = \log_e x  (Natural Logarithm)
  • log⁡x=log⁡10x\log x = \log_{10} x  (Common Logarithm), where e≈2.718281828…e \approx 2.718281828 \ldots 

Logarithm Properties

  1. log⁡bb=1\log_b b = 1 
  2. log⁡b1=0\log_b 1 = 0 
  3. log⁡b(bx)=x\log_b (b^x) = x 
  4. blog⁡bx=xb^{\log_b x} = x 
  5. log⁡b(xr)=r⋅log⁡b 
  6. log⁡b(xy)=log⁡bx+log⁡b 
  7. log⁡b(xy)=log⁡bx−log⁡b 

Domain of the Logarithmic Function

The domain of log⁡bx\log_b x  is x>0x > 0 .

Factoring and Solving

Factoring Formulas

  1. x2−a2=(x+a)(x−a)x^2 – a^2 = (x + a)(x – a) 
  2. x2+2ax+a2=(x+a)2x^2 + 2ax + a^2 = (x + a)^2 
  3. x2−2ax+a2=(x−a)2x^2 – 2ax + a^2 = (x – a)^2 
  4. x2+(a+b)x+ab=(x+a)(x+b)x^2 + (a + b)x + ab = (x + a)(x + b) 
  5. x3+3ax2+3a2x+a3=(x+a)3x^3 + 3ax^2 + 3a^2x + a^3 = (x + a)^3 
  6. x3−3ax2+3a2x−a3=(x−a)3x^3 – 3ax^2 + 3a^2x – a^3 = (x – a)^3 
  7. x3+a3=(x+a)(x2−ax+a2)x^3 + a^3 = (x + a)(x^2 – ax + a^2) 
  8. x3−a3=(x−a)(x2+ax+a2)x^3 – a^3 = (x – a)(x^2 + ax + a^2) 
  9. x2n−a2n=(xn−an)(xn+an)x^{2n} – a^{2n} = (x^n – a^n)(x^n + a^n) 
    • If nn  is odd, then:
      • xn−an=(x−a)(xn−1+axn−2+⋯+an−1)x^n – a^n = (x – a)(x^{n-1} + ax^{n-2} + \cdots + a^{n-1}) 
      • xn+an=(x+a)(xn−1−axn−2+a2xn−3−⋯+an−1)x^n + a^n = (x + a)(x^{n-1} – ax^{n-2} + a^2x^{n-3} – \cdots + a^{n-1}) 

Quadratic Formula

To solve the quadratic equation ax2+bx+c=0ax^2 + bx + c = 0 , where a≠0a \neq 0 :   x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}
  • If b2−4ac>0b^2 – 4ac > 0  – Two real, unequal solutions.
  • If b2−4ac=0b^2 – 4ac = 0  – One repeated real solution.
  • If b2−4ac<0b^2 – 4ac < 0  – Two complex solutions.

Square Root Property

If x2=px^2 = p , then:   x=±px = \pm \sqrt{p}

Absolute Value Equations/Inequalities

If bb  is a positive number:

  1. ∣p∣=b  ⟹  p=−b|p| = b \implies p = -b  or p=bp = b 
  2. ∣p∣<b  ⟹  −b<p<b|p| < b \implies -b < p < b 
  3. ∣p∣>b  ⟹  p<−b|p| > b \implies p < -b  or p>bp > b 

Completing the Square

Solve 2x2−6x−10=02x^2 – 6x – 10 = 0 

  1. Divide by the coefficient of x2x^2 :

    x2−3x−5=0x^2 – 3x – 5 = 0 

  2. Move the constant to the other side:

    x2−3x=5x^2 – 3x = 5 

  3. Take half the coefficient of xx , square it, and add it to both sides:

    x2−3x+(−32)2=5+(−32)2x^2 – 3x + \left(-\frac{3}{2}\right)^2 = 5 + \left(-\frac{3}{2}\right)^2 
    x2−3x+94=5+94=294x^2 – 3x + \frac{9}{4} = 5 + \frac{9}{4} = \frac{29}{4}

  4. Factor the left side:

    (x−32)2=294\left(x – \frac{3}{2}\right)^2 = \frac{29}{4}

  5. Use the Square Root Property:

    x−32=±294=±292x – \frac{3}{2} = \pm \sqrt{\frac{29}{4}} = \pm \frac{\sqrt{29}}{2}

  6. Solve for xx :

    x=32±292x = \frac{3}{2} \pm \frac{\sqrt{29}}{2}

Functions and Graphs

Constant Function
y=ay = a  or f(x)=af(x) = a 

  • Graph is a horizontal line passing through the point (0,a)(0, a) .

Parabola/Quadratic Function
x=ay2+by+cx = ay^2 + by + c  or g(y)=ay2+by+cg(y) = ay^2 + by + c 

  • The graph is a parabola that opens right if a>0a > 0  or left if a<0a < 0  and has a vertex at (g(−b2a),−b2a)\left(g\left(-\frac{b}{2a}\right), -\frac{b}{2a}\right) .

Line/Linear Function
y=mx+by = mx + b  or f(x)=mx+bf(x) = mx + b 

  • Graph is a line with point (0,b)(0, b)  and slope mm .

Slope

  • Slope of the line containing the two points (x1,y1)(x_1, y_1)  and (x2,y2)(x_2, y_2) is given by: m=y2−y1x2−x1=riserunm = \frac{y_2 – y_1}{x_2 – x_1} = \frac{\text{rise}}{\text{run}}

Slope – Intercept Form

  • The equation of the line with slope mm and y-intercept (0,b)(0, b)  is: y=mx+by = mx + b 

Circle
(x−h)2+(y−k)2=r2(x – h)^2 + (y – k)^2 = r^2 

  • Graph is a circle with radius rr  and center (h,k)(h, k) .

Ellipse

(x−h)2a2+(y−k)2b2=1\frac{(x – h)^2}{a^2} + \frac{(y – k)^2}{b^2} = 1 

  • Graph is an ellipse with center (h,k)(h, k) , with vertices aa units left/right from the center and vertices bb  units up/down from the center.

Hyperbola

(x−h)2a2−(y−k)2b2=1\frac{(x – h)^2}{a^2} – \frac{(y – k)^2}{b^2} = 1 

  • Graph is a hyperbola that opens left and right, has a center at (h,k)(h, k) , vertices aa units left/right of the center, and asymptotes that pass through the center with slope ±ba\pm \frac{b}{a} .

Point – Slope Form

  • The equation of the line with slope mm and passing through the point (x1,y1)(x_1, y_1)  is: y=y1+m(x−x1)y = y_1 + m(x – x_1) 

Hyperbola

(x−h)2a2−(y−k)2b2=1\frac{(x – h)^2}{a^2} – \frac{(y – k)^2}{b^2} = 1 

  • Graph is a hyperbola that opens up and down, has a center at (h,k)(h, k) , vertices bb  units up/down from the center, and asymptotes that pass through the center with slope ±ba\pm \frac{b}{a} .

Parabola/Quadratic Function

  • Equation:

    y=a(x−h)2+korf(x)=a(x−h)2+ky = a(x – h)^2 + k \quad \text{or} \quad f(x) = a(x – h)^2 + k 
    • The graph is a parabola that opens up if a>0a > 0  or down if a<0a < 0  and has a vertex at (h,k)(h, k) .

  • Another form:

    y=ax2+bx+corf(x)=ax2+bx+cy = ax^2 + bx + c \quad \text{or} \quad f(x) = ax^2 + bx + c 
    • The graph is a parabola that opens up if a>0a > 0  or down if a<0a < 0  and has a vertex at (−b2a,f(−b2a))\left(-\frac{b}{2a}, f\left(-\frac{b}{2a}\right)\right) .

Common Algebraic Errors

Error Reason/Correct/Justification/Example
20=0\frac{2}{0} = 0  and 20≠2\frac{2}{0} \neq 2 Division by zero is undefined!
−32≠9-3^2 \neq 9 −32=−9-3^2 = -9, (−3)2=9(-3)^2 = 9. Watch parenthesis!
(x2)3≠x5(x^2)^3 \neq x^5 (x2)3=x2×x2×x2=x6(x^2)^3 = x^2 \times x^2 \times x^2 = x^6
ab+c≠ab+ac\frac{a}{b+c} \neq \frac{a}{b} + \frac{a}{c} 12=11+1≠11+11=2\frac{1}{2} = \frac{1}{1+1} \neq \frac{1}{1} + \frac{1}{1} = 2
1x2+x3≠x−2+x−3\frac{1}{x^2 + x^3} \neq x^{-2} + x^{-3} A more complex version of the previous error.
a+bxa≠1+b  a+bxa=aa+bxa=1+bxa\frac{a+bx}{a} = \frac{a}{a} + \frac{bx}{a} = 1 + \frac{bx}{a}. Beware of incorrect cancelling!
−a(x−1)≠−ax−a-a(x-1) \neq -ax – a −a(x−1)=−ax+a-a(x-1) = -ax + a. Make sure you distribute the “-“ correctly!
(x+a)2≠x2+a2(x+a)^2 \neq x^2 + a^2 (x+a)2=(x+a)(x+a)=x2+2ax+a2(x+a)^2 = (x + a)(x + a) = x^2 + 2ax + a^2
x2+a2≠x+a\sqrt{x^2 + a^2} \neq x + a Example: 5 = 25=32+42≠32+42=3+4=7\sqrt{25} = \sqrt{3^2 + 4^2} \neq \sqrt{3^2} + \sqrt{4^2} = 3 + 4 = 7
x+a≠x+a\sqrt{x + a} \neq \sqrt{x} + \sqrt{a} See previous error for similar reasoning.
(x+a)n≠xn+an(x + a)^n \neq x^n + a^n  and x+an≠xn+an\sqrt[n]{x + a} \neq \sqrt[n]{x} + \sqrt[n]{a} More general version of previous errors.
2(x+1)2≠(2x+2)22(x+1)^2 \neq (2x+2)^2 2(x+1)2=2(x2+2x+1)=2x2+4x+22(x+1)^2 = 2(x^2 + 2x + 1) = 2x^2 + 4x + 2  while (2x+2)2=4x2+8x+4(2x+2)^2 = 4x^2 + 8x + 4. Remember to square first, then distribute!
(2x+2)2≠2(x+1)2(2x+2)^2 \neq 2(x+1)^2 See the previous example. You cannot factor out a constant if there is a power on the parentheses!
−x2+a2≠−x2+a2\sqrt{-x^2 + a^2} \neq -\sqrt{x^2 + a^2} −x2+a2=(−x2+a2)1/2\sqrt{-x^2 + a^2} = (-x^2 + a^2)^{1/2}. Now refer to the previous errors for proper handling of square roots.
a(bc)≠abc\frac{a}{\left(\frac{b}{c}\right)} \neq \frac{ab}{c} a(bc)=(a1)÷(bc)=(a1)⋅(cb)=acb\frac{a}{\left(\frac{b}{c}\right)} = \left(\frac{a}{1}\right) \div \left(\frac{b}{c}\right) = \left(\frac{a}{1}\right) \cdot \left(\frac{c}{b}\right) = \frac{ac}{b}
(ab)c≠acb\frac{\left(\frac{a}{b}\right)}{c} \neq \frac{ac}{b} (ab)c=(ab)(c1)=(ab)×(1c)=abc\frac{\left(\frac{a}{b}\right)}{c} = \frac{\left(\frac{a}{b}\right)}{\left(\frac{c}{1}\right)} = \left(\frac{a}{b}\right) \times \left(\frac{1}{c}\right) = \frac{a}{bc}

Limits Definitions

Precise Definition: We say lim⁡x→af(x)=L\lim_{{x \to a}} f(x) = L if for every ϵ>0\epsilon > 0  there is a δ>0\delta > 0  such that whenever 0<∣x−a∣<δ0 < |x – a| < \delta then ∣f(x)−L∣<ϵ|f(x) – L| < \epsilon .

Working Definition: We say lim⁡x→af(x)=L\lim_{{x \to a}} f(x) = L if we can make f(x)f(x)  as close to LL  as we want by taking xx  sufficiently close to aa  (on either side of aa ) without letting x=ax = a .

Right Hand Limit: lim⁡x→a+f(x)=L\lim_{{x \to a^+}} f(x) = L . This has the same definition as the limit except it requires x>ax > a .

Left Hand Limit: lim⁡x→a−f(x)=L\lim_{{x \to a^-}} f(x) = L . This has the same definition as the limit except it requires x<ax < a .

Limit at Infinity: We say lim⁡x→∞f(x)=L\lim_{{x \to \infty}} f(x) = L  if we can make f(x)f(x) as close to LL  as we want by taking xx  large enough and positive.
There is a similar definition for lim⁡x→−∞f(x)=L\lim_{{x \to -\infty}} f(x) = L  except we require xx  to be large and negative.

Infinite Limit: We say lim⁡x→af(x)=∞\lim_{{x \to a}} f(x) = \infty  if we can make f(x)f(x)  arbitrarily large (and positive) by taking xx  sufficiently close to aa  (on either side of aa ) without letting x=ax = a .
There is a similar definition for lim⁡x→af(x)=−∞\lim_{{x \to a}} f(x) = -\infty  except we make f(x)f(x)  arbitrarily large and negative.

Relationship between the Limit and One-Sided Limits

lim⁡x→af(x)=L⇒lim⁡x→a+f(x)=lim⁡x→a−f(x)=L\lim_{{x \to a}} f(x) = L \Rightarrow \lim_{{x \to a^+}} f(x) = \lim_{{x \to a^-}} f(x) = L 
lim⁡x→a+f(x)=lim⁡x→a−f(x)=L⇒lim⁡x→af(x)=L\lim_{{x \to a^+}} f(x) = \lim_{{x \to a^-}} f(x) = L \Rightarrow \lim_{{x \to a}} f(x) = L 
lim⁡x→a+f(x)≠lim⁡x→a−f(x)⇒lim⁡x→af(x) Does Not Exist\lim_{{x \to a^+}} f(x) \neq \lim_{{x \to a^-}} f(x) \Rightarrow \lim_{{x \to a}} f(x) \text{ Does Not Exist} 

Properties

Assume lim⁡x→af(x)\lim_{{x \to a}} f(x)  and lim⁡x→ag(x)\lim_{{x \to a}} g(x) both exist and cc  is any number, then:

  1. lim⁡x→a[cf(x)]=c⋅lim⁡x→af(x)\lim_{{x \to a}} [cf(x)] = c \cdot \lim_{{x \to a}} f(x) 
  2. lim⁡x→a[f(x)±g(x)]=lim⁡x→af(x)±lim⁡x→ag(x)\lim_{{x \to a}} [f(x) \pm g(x)] = \lim_{{x \to a}} f(x) \pm \lim_{{x \to a}} g(x) 
  3. lim⁡x→a[f(x)g(x)]=lim⁡x→af(x)⋅lim⁡x→ag(x)\lim_{{x \to a}} [f(x)g(x)] = \lim_{{x \to a}} f(x) \cdot \lim_{{x \to a}} g(x) 
  4. lim⁡x→a[f(x)g(x)]=lim⁡x→af(x)lim⁡x→ag(x)\lim_{{x \to a}} \left[\frac{f(x)}{g(x)}\right] = \frac{\lim_{{x \to a}} f(x)}{\lim_{{x \to a}} g(x)} provided lim⁡x→ag(x)≠0\lim_{{x \to a}} g(x) \neq 0 
  5. lim⁡x→a[f(x)]n=[lim⁡x→af(x)]n\lim_{{x \to a}} [f(x)]^n = \left[\lim_{{x \to a}} f(x)\right]^n 
  6. lim⁡x→a[f(x)n]=lim⁡x→af(x)n\lim_{{x \to a}} \left[\sqrt[n]{f(x)}\right] = \sqrt[n]{\lim_{{x \to a}} f(x)}

Basic Limit Evaluations at ±∞\pm \infty 

Note: sgn(a)=1\text{sgn}(a) = 1  if a>0a > 0  and sgn(a)=−1\text{sgn}(a) = -1  if a<0a < 0 .

  1. lim⁡x→∞ex=∞\lim_{{x \to \infty}} e^x = \infty  and lim⁡x→−∞ex=0\lim_{{x \to -\infty}} e^x = 0 
  2. lim⁡x→∞ln⁡(x)=∞\lim_{{x \to \infty}} \ln(x) = \infty  and lim⁡x→0+ln⁡(x)=−∞\lim_{{x \to 0^+}} \ln(x) = -\infty 
  3. If r>0r > 0, then lim⁡x→∞bxr=0\lim_{{x \to \infty}} \frac{b}{x^r} = 0 
  4. If r>0r > 0 and xrx^r  is real for negative xx , then lim⁡x→−∞bxr=0\lim_{{x \to -\infty}} \frac{b}{x^r} = 0
  5. nn  even: lim⁡x→±∞xn=∞\lim_{{x \to \pm \infty}} x^n = \infty 
  6. nn  odd: lim⁡x→∞xn=∞\lim_{{x \to \infty}} x^n = \infty  and lim⁡x→−∞xn=−∞\lim_{{x \to -\infty}} x^n = -\infty 
  7. nn  even: lim⁡x→±∞axn+⋯+bx+c=sgn(a)⋅∞\lim_{{x \to \pm \infty}} ax^n + \cdots + bx + c = \text{sgn}(a) \cdot \infty 
  8. nn  odd: lim⁡x→∞axn+⋯+bx+c=sgn(a)⋅∞\lim_{{x \to \infty}} ax^n + \cdots + bx + c = \text{sgn}(a) \cdot \infty 
  9. nn  odd: lim⁡x→−∞axn+⋯+cx+d=−sgn(a)⋅∞\lim_{{x \to -\infty}} ax^n + \cdots + cx + d = -\text{sgn}(a) \cdot \infty 

Evaluation Techniques

Continuous Functions
If f(x)f(x)  is continuous at aa  then:

lim⁡x→af(x)=f(a)\lim_{{x \to a}} f(x) = f(a) 

L’Hôpital’s Rule
If lim⁡x→af(x)g(x)=00\lim_{{x \to a}} \frac{f(x)}{g(x)} = \frac{0}{0}  or lim⁡x→af(x)g(x)=±∞±∞\lim_{{x \to a}} \frac{f(x)}{g(x)} = \frac{\pm \infty}{\pm \infty}, then:

lim⁡x→af(x)g(x)=lim⁡x→af′(x)g′(x)\lim_{{x \to a}} \frac{f(x)}{g(x)} = \lim_{{x \to a}} \frac{f'(x)}{g'(x)}

where aa  is a number, ∞\infty , or −∞-\infty .

Continuous Functions and Composition
If f(x)f(x) is continuous at bb  and lim⁡x→ag(x)=b\lim_{{x \to a}} g(x) = b , then:

lim⁡x→af(g(x))=f(lim⁡x→ag(x))=f(b)\lim_{{x \to a}} f(g(x)) = f\left(\lim_{{x \to a}} g(x)\right) = f(b) 

Polynomials at Infinity
For polynomials p(x)p(x)  and q(x)q(x) , to compute lim⁡x→±∞p(x)q(x)\lim_{{x \to \pm \infty}} \frac{p(x)}{q(x)} , factor the largest power of xx out of both p(x)p(x)  and q(x)q(x) and then compute the limit. Example:

lim⁡x→−∞3x2−45x−2x2=lim⁡x→−∞x2(3−4x2)x2(5x−2)=lim⁡x→−∞3−4x25x−2=32\lim_{{x \to -\infty}} \frac{3x^2 – 4}{5x – 2x^2} = \lim_{{x \to -\infty}} \frac{x^2(3 – \frac{4}{x^2})}{x^2(\frac{5}{x} – 2)} = \lim_{{x \to -\infty}} \frac{3 – \frac{4}{x^2}}{\frac{5}{x} – 2} = \frac{3}{2}

Factor and Cancel

lim⁡x→2x2+4x−12x2−2x=lim⁡x→2(x−2)(x+6)x(x−2)=lim⁡x→2x+6x=82=4\lim_{{x \to 2}} \frac{x^2 + 4x – 12}{x^2 – 2x} = \lim_{{x \to 2}} \frac{(x – 2)(x + 6)}{x(x – 2)} = \lim_{{x \to 2}} \frac{x + 6}{x} = \frac{8}{2} = 4 

Rationalize Numerator/Denominator

lim⁡x→93−xx2−81=lim⁡x→9(3−x)(3+x)(x2−81)(3+x)=lim⁡x→99−x(x+9)(3+x)=lim⁡x→9−1(x+9)(3+x)=−118⋅6=−1108\lim_{{x \to 9}} \frac{3 – \sqrt{x}}{x^2 – 81} = \lim_{{x \to 9}} \frac{(3 – \sqrt{x})(3 + \sqrt{x})}{(x^2 – 81)(3 + \sqrt{x})} = \lim_{{x \to 9}} \frac{9 – x}{(x + 9)(3 + \sqrt{x})} = \lim_{{x \to 9}} \frac{-1}{(x + 9)(3 + \sqrt{x})} = \frac{-1}{18 \cdot 6} = -\frac{1}{108}

Piecewise Function

lim⁡x→−2g(x)whereg(x)={x2+5if x<−21−3xif x≥−2\lim_{{x \to -2}} g(x) \quad \text{where} \quad g(x) = \begin{cases} x^2 + 5 & \text{if } x < -2 \\ 1 – 3x & \text{if } x \geq -2 \end{cases}

Compute two one-sided limits:

lim⁡x→−2−g(x)=lim⁡x→−2−(x2+5)=9andlim⁡x→−2+g(x)=lim⁡x→−2+(1−3x)=7\lim_{{x \to -2^-}} g(x) = \lim_{{x \to -2^-}} (x^2 + 5) = 9 \quad \text{and} \quad \lim_{{x \to -2^+}} g(x) = \lim_{{x \to -2^+}} (1 – 3x) = 7 

Since the one-sided limits are different, lim⁡x→−2g(x)\lim_{{x \to -2}} g(x) does not exist. If the two one-sided limits had been equal, then lim⁡x→−2g(x)\lim_{{x \to -2}} g(x) would have existed and had the same value.

Combine Rational Expressions

lim⁡h→01h(1x+h−1x)=lim⁡h→01h(x−(x+h)x(x+h))=lim⁡h→01h(−hx(x+h))=lim⁡h→0−1x(x+h)=−1x2\lim_{{h \to 0}} \frac{1}{h} \left( \frac{1}{x + h} – \frac{1}{x} \right) = \lim_{{h \to 0}} \frac{1}{h} \left( \frac{x – (x + h)}{x(x + h)} \right) = \lim_{{h \to 0}} \frac{1}{h} \left( \frac{-h}{x(x + h)} \right) = \lim_{{h \to 0}} \frac{-1}{x(x + h)} = -\frac{1}{x^2}

Some Continuous Functions

Partial list of continuous functions and the values of xx  for which they are continuous:

  1. Polynomials — Continuous for all xx .
  2. Rational functions — Continuous except for values of xx  that give division by zero.
  3. xn\sqrt[n]{x}  (where nn  is odd) — Continuous for all xx .
  4. xn\sqrt[n]{x}  (where nn  is even) — Continuous for all x≥0x \geq 0 .
  5. exe^x  — Continuous for all xx .
  6. ln⁡(x)\ln(x)  — Continuous for x>0x > 0 .
  7. cos⁡(x)\cos(x)  and sin⁡(x)\sin(x)  — Continuous for all xx .
  8. tan⁡(x)\tan(x) and sec⁡(x)\sec(x)  — Continuous provided x≠…,−3π2,−π2,π2,3π2,…x \neq \ldots, -\frac{3\pi}{2}, -\frac{\pi}{2}, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots 
  9. cot⁡(x)\cot(x)  and csc⁡(x)\csc(x)  — Continuous provided x≠…,−2π,−π,0,π,2π,…x \neq \ldots, -2\pi, -\pi, 0, \pi, 2\pi, \ldots 

Intermediate Value Theorem

Suppose that f(x)f(x)  is continuous on [a,b][a, b] and let MM  be any number between f(a)f(a) and f(b)f(b) .
Then, there exists a number cc  such that a<c<ba < c < b and f(c)=Mf(c) = M .

Derivatives

Definition and Notation
If y=f(x)y = f(x) , then the derivative is defined to be:

f′(x)=lim⁡h→0f(x+h)−f(x)hf'(x) = \lim_{{h \to 0}} \frac{{f(x+h) – f(x)}}{h}

If y=f(x)y = f(x) , then all of the following are equivalent notations for the derivative:

f′(x)=y′=dfdx=dydx=ddx(f(x))=Df(x)f'(x) = y’ = \frac{{df}}{{dx}} = \frac{{dy}}{{dx}} = \frac{{d}}{{dx}} (f(x)) = Df(x) 

If y=f(x)y = f(x) , all of the following are equivalent notations for the derivative evaluated at x=ax = a :

f′(a)=y′∣x=a=dfdx∣x=a=dydx∣x=a=Df(a)f'(a) = \left. y’ \right|_{x = a} = \left. \frac{{df}}{{dx}} \right|_{x = a} = \left. \frac{{dy}}{{dx}} \right|_{x = a} = Df(a) 

Interpretation of the Derivative

If y=f(x)y = f(x) , then:

  • m=f′(a)m = f'(a) is the slope of the tangent line to y=f(x)y = f(x) at x=ax = a  and the equation of the tangent line at x=ax = a  is given by:

    y=f(a)+f′(a)(x−a)y = f(a) + f'(a)(x – a) 

  • f′(a)f'(a)  is the instantaneous rate of change of f(x)f(x)  at x=ax = a .

  • If f(x)f(x)  is the position of an object at time xx , then f′(a)f'(a)  is the velocity of the object at x=ax = a .

Basic Properties and Formulas

If f(x)f(x) and g(x)g(x) are differentiable functions (the derivative exists), and cc and nn are any real numbers:

  1. (cf)′=cf′(x)(cf)’ = cf'(x) 
  2. (f±g)′=f′(x)±g′(x)(f \pm g)’ = f'(x) \pm g'(x) 
  3. (fg)′=f′g+fg′(fg)’ = f’g + fg’      (Product Rule)
  4. (fg)′=f′g−fg′g2\left( \frac{f}{g} \right)’ = \frac{f’g – fg’}{g^2}     (Quotient Rule)
  5. ddx(c)=0\frac{d}{dx}(c) = 0 
  6. ddx(xn)=nxn−1\frac{d}{dx}(x^n) = nx^{n-1}      (Power Rule)
  7. ddx(f(g(x)))=f′(g(x))⋅g′(x)\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)      (Chain Rule)

Common Derivatives

  1. ddx(x)=1\frac{d}{dx}(x) = 1 
  2. ddx(sin⁡x)=cos⁡x\frac{d}{dx}(\sin x) = \cos x 
  3. ddx(cos⁡x)=−sin⁡x\frac{d}{dx}(\cos x) = -\sin x 
  4. ddx(tan⁡x)=sec⁡2x\frac{d}{dx}(\tan x) = \sec^2 x 
  5. ddx(sec⁡x)=sec⁡x⋅tan⁡x\frac{d}{dx}(\sec x) = \sec x \cdot \tan x
  6. ddx(csc⁡x)=−csc⁡x⋅cot⁡x\frac{d}{dx}(\csc x) = -\csc x \cdot \cot x 
  7. ddx(cot⁡x)=−csc⁡2x\frac{d}{dx}(\cot x) = -\csc^2 x 
  8. ddx(sin⁡−1x)=11−x2\frac{d}{dx}(\sin^{-1} x) = \frac{1}{\sqrt{1 – x^2}}
  9. ddx(cos⁡−1x)=−11−x2\frac{d}{dx}(\cos^{-1} x) = -\frac{1}{\sqrt{1 – x^2}}
  10. ddx(tan⁡−1x)=11+x2\frac{d}{dx}(\tan^{-1} x) = \frac{1}{1 + x^2}
  11. ddx(ax)=axln⁡(a)\frac{d}{dx}(a^x) = a^x \ln(a) 
  12. ddx(ex)=ex\frac{d}{dx}(e^x) = e^x 
  13. ddx(ln⁡(x))=1x\frac{d}{dx}(\ln(x)) = \frac{1}{x}  for x>0x > 0 
  14. ddx(ln⁡∣x∣)=1x\frac{d}{dx}(\ln|x|) = \frac{1}{x}  for x≠0x \neq 0 
  15. ddx(log⁡a(x))=1xln⁡(a)\frac{d}{dx}(\log_a(x)) = \frac{1}{x \ln(a)}  for x>0x > 0 

Chain Rule Variants

The chain rule applied to some specific functions:

  1. ddx([f(x)]n)=n[f(x)]n−1f′(x)\frac{d}{dx} \left( [f(x)]^n \right) = n[f(x)]^{n-1} f'(x) 
  2. ddx(ef(x))=f′(x)ef(x)\frac{d}{dx} \left( e^{f(x)} \right) = f'(x) e^{f(x)} 
  3. ddx(ln⁡[f(x)])=f′(x)f(x)\frac{d}{dx} \left( \ln[f(x)] \right) = \frac{f'(x)}{f(x)}
  4. ddx(sin⁡[f(x)])=f′(x)cos⁡[f(x)]\frac{d}{dx} \left( \sin[f(x)] \right) = f'(x) \cos[f(x)] 
  5. ddx(cos⁡[f(x)])=−f′(x)sin⁡[f(x)]\frac{d}{dx} \left( \cos[f(x)] \right) = -f'(x) \sin[f(x)] 
  6. ddx(tan⁡[f(x)])=f′(x)sec⁡2[f(x)]\frac{d}{dx} \left( \tan[f(x)] \right) = f'(x) \sec^2[f(x)] 
  7. ddx(sec⁡[f(x)])=f′(x)sec⁡[f(x)]tan⁡[f(x)]\frac{d}{dx} \left( \sec[f(x)] \right) = f'(x) \sec[f(x)] \tan[f(x)] 
  8. ddx(tan⁡−1[f(x)])=f′(x)1+[f(x)]2\frac{d}{dx} \left( \tan^{-1}[f(x)] \right) = \frac{f'(x)}{1 + [f(x)]^2}

Higher Order Derivatives

The second derivative is denoted as:

f′′(x)=f(2)(x)=d2fdx2f”(x) = f^{(2)}(x) = \frac{d^2f}{dx^2}

and is defined as:

f′′(x)=(f′(x))′f”(x) = (f'(x))’ 

i.e., the derivative of the first derivative, f′(x)f'(x) .

The nthn^{th}  derivative is denoted as:

f(n)(x)=dnfdxnf^{(n)}(x) = \frac{d^n f}{dx^n}

and is defined as:

f(n)(x)=(f(n−1)(x))′f^{(n)}(x) = (f^{(n-1)}(x))’ 

i.e., the derivative of the (n−1)st(n-1)^{st} derivative, f(n−1)(x)f^{(n-1)}(x) .

Implicit Differentiation

Find y′y’  if:

e2x−9y+x3y2=sin⁡(y)+11xe^{2x – 9y} + x^3 y^2 = \sin(y) + 11x 

Remember y=y(x)y = y(x)  here, so products/quotients of xx  and yy  will use the product/quotient rule and derivatives of yy will use the chain rule. The trick is to differentiate as normal and every time you differentiate a yy , you tack on a y′y’  (from the chain rule). After differentiating, solve for y′y’ .

e2x−9y(2−9y′)+3x2y2+2x3yy′=cos⁡(y)y′+11e^{2x – 9y}(2 – 9y’) + 3x^2 y^2 + 2x^3 y y’ = \cos(y) y’ + 11 
2e2x−9y−9y′e2x−9y+3x2y2+2x3yy′=cos⁡(y)y′+112e^{2x – 9y} – 9y’ e^{2x – 9y} + 3x^2 y^2 + 2x^3 y y’ = \cos(y) y’ + 11 
(2x3y−9e2x−9y−cos⁡(y))y′=11−2e2x−9y−3x2y2(2x^3 y – 9e^{2x – 9y} – \cos(y)) y’ = 11 – 2e^{2x – 9y} – 3x^2 y^2 
y′=11−2e2x−9y−3x2y22x3y−9e2x−9y−cos⁡(y)y’ = \frac{11 – 2e^{2x – 9y} – 3x^2 y^2}{2x^3 y – 9e^{2x – 9y} – \cos(y)}

Increasing/Decreasing & Concave Up/Concave Down

Critical Points

x=cx = c  is a critical point of f(x)f(x) provided either:

  1. f′(c)=0f'(c) = 0 
  2. f′(c)f'(c)  does not exist.

Increasing/Decreasing

  1. If f′(x)>0f'(x) > 0  for all xx  in an interval II  then f(x)f(x)  is increasing on the interval II .
  2. If f′(x)<0f'(x) < 0  for all xx  in an interval II  then f(x)f(x)  is decreasing on the interval II .
  3. If f′(x)=0f'(x) = 0  for all xx  in an interval II  then f(x)f(x) is constant on the interval II .

Concave Up/Concave Down

  1. If f′′(x)>0f”(x) > 0  for all xx  in an interval II , then f(x)f(x)  is concave up on the interval II.
  2. If f′′(x)<0f”(x) < 0  for all xx  in an interval II , then f(x)f(x)  is concave down on the interval II.

Inflection Points

x=cx = c  is an inflection point of f(x)f(x)  if the concavity changes at x=cx = c .

Extrema

Absolute Extrema

  1. x=cx = c  is an absolute maximum of f(x)f(x) if f(c)≥f(x)f(c) \geq f(x)  for all xx  in the domain.
  2. x=cx = c  is an absolute minimum of f(x)f(x)  if f(c)≤f(x)f(c) \leq f(x)  for all xx  in the domain.

Fermat’s Theorem

If f(x)f(x)  has a relative (or local) extrema at x=cx = c , then x=cx = c  is a critical point of f(x)f(x) .

Extreme Value Theorem

If f(x)f(x)  is continuous on the closed interval [a,b][a, b] , then there exist numbers cc  and dd  such that:

  1. a≤c,d≤ba \leq c, d \leq b 
  2. f(c)f(c)  is the absolute maximum in [a,b][a, b] 
  3. f(d)f(d) is the absolute minimum in [a,b][a, b] 

Finding Absolute Extrema

To find the absolute extrema of the continuous function f(x)f(x)  on the interval [a,b][a, b] , use the following process:

  1. Find all critical points of f(x)f(x)  in [a,b][a, b] .
  2. Evaluate f(x)f(x)  at all points found in Step 1.
  3. Evaluate f(a)f(a)  and f(b)f(b) .
  4. Identify the absolute maximum (largest function value) and the absolute minimum (smallest function value) from the evaluations in Steps 2 & 3.

Relative (Local) Extrema

  1. x=cx = c  is a relative (or local) maximum of f(x)f(x)  if f(c)≥f(x)f(c) \geq f(x)  for all xx  near cc .
  2. x=cx = c  is a relative (or local) minimum of f(x)f(x) if f(c)≤f(x)f(c) \leq f(x)  for all xx  near cc .

First Derivative Test

If x=cx = c  is a critical point of f(x)f(x) then x=cx = c  is:

  1. a relative maximum of f(x)f(x)  if f′(x)>0f'(x) > 0  to the left of x=cx = c  and f′(x)<0f'(x) < 0  to the right of x=cx = c .
  2. a relative minimum of f(x)f(x)  if f′(x)<0f'(x) < 0  to the left of x=cx = c  and f′(x)>0f'(x) > 0  to the right of x=cx = c .
  3. not a relative extrema of f(x)f(x)  if f′(x)f'(x)  is the same sign on both sides of x=cx = c .

Second Derivative Test

If x=cx = c  is a critical point of f(x)f(x)  such that f′(c)=0f'(c) = 0  then x=cx = c :

  1. is a relative maximum of f(x)f(x)  if f′′(c)<0f”(c) < 0 .
  2. is a relative minimum of f(x)f(x)  if f′′(c)>0f”(c) > 0 .
  3. may be a relative maximum, relative minimum, or neither if f′′(c)=0f”(c) = 0 .

Finding Relative Extrema and/or Classifying Critical Points

  1. Find all critical points of f(x)f(x) .
  2. Use the first derivative test or the second derivative test on each critical point.

Mean Value Theorem

If f(x)f(x)  is continuous on the closed interval [a,b][a, b]  and differentiable on the open interval (a,b)(a, b) , then there is a number a<c<ba < c < b  such that:

f′(c)=f(b)−f(a)b−af'(c) = \frac{f(b) – f(a)}{b – a}

Newton’s Method

If xnx_n is the nn-th guess for the root/solution of f(x)=0f(x) = 0 , then the (n+1)(n+1)-st guess is given by:

xn+1=xn−f(xn)f′(xn)x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}

provided f′(xn)f'(x_n) exists.

Related Rates

Procedure:

  1. Sketch a picture and identify known and unknown quantities.
  2. Write down an equation relating the quantities.
  3. Differentiate the equation with respect to tt using implicit differentiation (i.e., include a derivative every time you differentiate a function of tt).
  4. Plug in known quantities and solve for the unknown quantity.

Example 1: Ladder Problem

  • Problem Statement: A 15-foot ladder is resting against a wall. The bottom is initially 10 ft away and is being pushed towards the wall at 14\frac{1}{4}  ft/sec. How fast is the top of the ladder moving after 12 seconds? Sketch picture and identify known/unknown quantities.
  • Solution:
    • Let xx  be the distance from the wall to the bottom of the ladder and yy  be the height of the top of the ladder above the ground.
    • Given: dxdt=−14\frac{dx}{dt} = -\frac{1}{4}  ft/sec (negative because xx  is decreasing).
    • Use the Pythagorean Theorem: x2+y2=152x^2 + y^2 = 15^2   
    • Differentiate with respect to tt  : 2xdxdt+2ydydt=02x \frac{dx}{dt} + 2y \frac{dy}{dt} = 0   
    • After 12 seconds, x=10−12(14)=7x = 10 – 12 \left(\frac{1}{4}\right) = 7  ft. To find yy  : y=152−72=176y = \sqrt{15^2 – 7^2} = \sqrt{176} 
    • Substitute values and solve for dydt\frac{dy}{dt}  : 7(−14)+176dydt=0  ⟹  dydt=74176 ft/sec7 \left(-\frac{1}{4}\right) + \sqrt{176} \frac{dy}{dt} = 0 \implies \frac{dy}{dt} = \frac{7}{4 \sqrt{176}} \text{ ft/sec}   

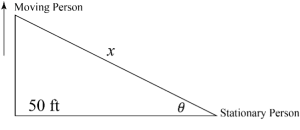
Example 2: Changing Angle Problem

  • Problem Statement: Two people are 50 ft apart when one starts walking north. The angle θ\thetachanges at 0.01 rad/min. At what rate is the distance between them changing when θ=0.5\theta = 0.5rad? Sketch picture and identify known/unknown quantities.
  • Solution:
    • Let xx  be the distance between the two people.
    • Given: dθdt=0.01\frac{d\theta}{dt} = 0.01  rad/min.
    • Use the trigonometric function: sec⁡θ=x50\sec \theta = \frac{x}{50} 
    • Differentiate with respect to tt  : sec⁡θtan⁡θdθdt=dxdt⋅150\sec \theta \tan \theta \frac{d\theta}{dt} = \frac{dx}{dt} \cdot \frac{1}{50} 
    • Plug in known values: sec⁡(0.5)⋅tan⁡(0.5)⋅(0.01)=dxdt50\sec(0.5) \cdot \tan(0.5) \cdot (0.01) = \frac{\frac{dx}{dt}}{50} 
    • Solve for dxdt\frac{dx}{dt}  : dxdt=50⋅sec⁡(0.5)⋅tan⁡(0.5)⋅0.01≈0.3112 ft/sec\frac{dx}{dt} = 50 \cdot \sec(0.5) \cdot \tan(0.5) \cdot 0.01 \approx 0.3112 \text{ ft/sec}   
    • Note: Ensure the calculator is in radians mode for accurate results.

Optimization

Sketch picture if needed, write down equation to be optimized and constraint. Solve constraint for one of the two variables and plug into first equation. Find critical points of equation in range of variables and verify that they are min/max as needed.

Example 1: Maximizing Enclosed Area

Problem Statement: We are enclosing a rectangular field with 500 ft of fence material and one side of the field is a building. Determine dimensions that will maximize the enclosed area.

Optimization

  • Solution:
    • Let xx be the length and yy be the width of the field.
    • The constraint is given by: x+2y=500  ⟹  x=500−2yx + 2y = 500 \implies x = 500 – 2y 
    • The area to maximize is given by: A=xy=y(500−2y)=500y−2y2A = xy = y(500 – 2y) = 500y – 2y^2 
    • Differentiate to find critical points: A′=500−4y  ⟹  y=125A’ = 500 – 4y \implies y = 125 
    • By the second derivative test, this is a relative maximum. Find xx : x=500−2(125)=250x = 500 – 2(125) = 250 
    • Dimensions: The dimensions are 250×125250 \times 125 .

Example 2: Finding Closest Points on a Curve

Problem Statement: Determine point(s) on y=x2+1y = x^2 + 1 that are closest to 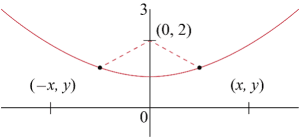(0,2)(0, 2) .
Optimization

  • Solution:
    • Minimize: f=d2=(x−0)2+(y−2)2f = d^2 = (x – 0)^2 + (y – 2)^2 
    • Constraint: y=x2+1y = x^2 + 1 . Substitute the constraint: f=x2+(y−2)2=y−1+(y−2)2=y2−3y+3f = x^2 + (y – 2)^2 = y – 1 + (y – 2)^2 = y^2 – 3y + 3 
    • Differentiate and find critical points: f′=2y−3  ⟹  y=32f’ = 2y – 3 \implies y = \frac{3}{2}
    • By the second derivative test, this is a relative minimum. Find xx values: x2=y−1=12  ⟹  x=±12x^2 = y – 1 = \frac{1}{2} \implies x = \pm \frac{1}{\sqrt{2}}
    • Points: The two points are: (12,32)and(−12,32)\left(\frac{1}{\sqrt{2}}, \frac{3}{2}\right) \quad \text{and} \quad \left(-\frac{1}{\sqrt{2}}, \frac{3}{2}\right) 

Integrals Definitions

Definite Integral:
Suppose f(x)f(x) is continuous on [a,b][a, b] . Divide [a,b][a, b] into nn subintervals of width Δx\Delta x and choose xi∗x_i^* from each interval. Then:

∫abf(x) dx=lim⁡n→∞∑i=1nf(xi∗)Δx\int_{a}^{b} f(x) \, dx = \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i^*) \Delta x 

Anti-Derivative:
An anti-derivative of f(x)f(x) is a function, F(x)F(x) , such that:

F′(x)=f(x)F'(x) = f(x) 

Indefinite Integral:

∫f(x) dx=F(x)+c\int f(x) \, dx = F(x) + c 

where F(x)F(x) is an anti-derivative of f(x)f(x) and cc is the constant of integration.

Fundamental Theorem of Calculus

Part I: If f(x)f(x) is continuous on [a,b][a, b] , then

g(x)=∫axf(t) dtg(x) = \int_{a}^{x} f(t) \, dt 

is also continuous on [a,b][a, b] and

g′(x)=ddx∫axf(t) dt=f(x).g'(x) = \frac{d}{dx} \int_{a}^{x} f(t) \, dt = f(x). 

Variants of Part I:

ddx∫au(x)f(t) dt=u′(x)f[u(x)]\frac{d}{dx} \int_{a}^{u(x)} f(t) \, dt = u'(x) f[u(x)]  
ddx∫v(x)bf(t) dt=−v′(x)f[v(x)]\frac{d}{dx} \int_{v(x)}^{b} f(t) \, dt = -v'(x) f[v(x)]  
ddx∫v(x)u(x)f(t) dt=u′(x)f[u(x)]−v′(x)f[v(x)]\frac{d}{dx} \int_{v(x)}^{u(x)} f(t) \, dt = u'(x) f[u(x)] – v'(x) f[v(x)] 

Part II: If f(x)f(x) is continuous on [a,b][a, b] and F(x)F(x) is an anti-derivative of f(x)f(x) (i.e., F(x)=∫f(x) dxF(x) = \int f(x) \, dx , then

∫abf(x) dx=F(b)−F(a).\int_{a}^{b} f(x) \, dx = F(b) – F(a). 

 

Algebra Cheat Sheet

Common Integrals

∫k dx=kx+c \int k \, dx = kx + c

∫xn dx=1n+1xn+1+c, n≠−1 \int x^n \, dx = \frac{1}{n+1} x^{n+1} + c, \, n \neq -1

∫x−1 dx=∫1x dx=ln⁡∣x∣+c \int x^{-1} \, dx = \int \frac{1}{x} \, dx = \ln|x| + c

∫1ax+b dx=1aln⁡∣ax+b∣+c \int \frac{1}{ax+b} \, dx = \frac{1}{a} \ln|ax + b| + c

∫ln⁡(u) du=uln⁡(u)−u+c \int \ln(u) \, du = u \ln(u) – u + c ∫eu du=eu+c \int e^u \, du = e^u + c

∫cos⁡u du=sin⁡u+c
∫sin⁡u du=−cos⁡u+c
∫sec⁡2u du=tan⁡u+c
∫sec⁡utan⁡u du=sec⁡u+c
∫csc⁡ucot⁡u du=−csc⁡u+c
∫csc⁡2u du=−cot⁡u+c

∫tan⁡u du=ln⁡∣sec⁡u∣+c\int \tan u \, du = \ln|\sec u| + c 

∫sec⁡u du=ln⁡∣sec⁡u+tan⁡u∣+c\int \sec u \, du = \ln|\sec u + \tan u| + c 

∫1a2+u2 du=1atan⁡−1(ua)+c\int \frac{1}{a^2 + u^2} \, du = \frac{1}{a} \tan^{-1}\left(\frac{u}{a}\right) + c 

∫1a2−u2 du=sin⁡−1(ua)+c\int \frac{1}{\sqrt{a^2 – u^2}} \, du = \sin^{-1}\left(\frac{u}{a}\right) + c 

Standard Integration Techniques

Note that at many schools, all but the Substitution Rule tend to be taught in a Calculus II class.

u-Substitution: The substitution u=g(x)u = g(x)  will convert

∫abf(g(x))g′(x)dx=∫g(a)g(b)f(u)du\int_a^b f(g(x)) g'(x) dx = \int_{g(a)}^{g(b)} f(u) du 

using du=g′(x)dxdu = g'(x) dx . For indefinite integrals, drop the limits of integration.

Let me know if you need any more formatting or explanations!

Example: ∫125x2cos⁡(x3)dx\int_{1}^{2} 5x^2 \cos(x^3) dx 

  1. Let u=x3u = x^3 , then du=3x2dxdu = 3x^2 dx or x2dx=13dux^2 dx = \frac{1}{3} du .
  2. Changing limits of integration:
    • When x=1x = 1: u=13=1u = 1^3 = 1 
    • When x=2x = 2: u=23=8u = 2^3 = 8 

∫125x2cos⁡(x3)dx=∫1853cos⁡(u)du\int_{1}^{2} 5x^2 \cos(x^3) dx = \int_{1}^{8} \frac{5}{3} \cos(u) du 
=53sin⁡(u)∣18=53(sin⁡(8)−sin⁡(1))= \left. \frac{5}{3} \sin(u) \right|_{1}^{8} = \frac{5}{3} \left( \sin(8) – \sin(1) \right) 

Integration by Parts:

∫u dv=uv−∫v duand∫abu dv=uv∣ab−∫abv du\int u \, dv = uv – \int v \, du \quad \text{and} \quad \int_{a}^{b} u \, dv = \left. uv \right|_{a}^{b} – \int_{a}^{b} v \, du 

To apply this method:

  • Choose uu  and dvdv  from the integral.
  • Compute dudu  by differentiating uu .
  • Compute vv  by integrating dvdv  using v=∫dvv = \int dv .

Example:
Evaluate ∫xe−x dx\int xe^{-x} \, dx .

  1. Choose u=xu = x  and dv=e−xdxdv = e^{-x} dx .
    Therefore, du=dxdu = dx  and v=−e−xv = -e^{-x} .

  2. Using the integration by parts formula:

    ∫xe−x dx=uv−∫v du\int xe^{-x} \, dx = uv – \int v \, du 
    ∫xe−x dx=−xe−x+∫e−x dx\int xe^{-x} \, dx = -xe^{-x} + \int e^{-x} \, dx 

  3. Integrate the remaining term:

    ∫xe−x dx=−xe−x−e−x+C\int xe^{-x} \, dx = -xe^{-x} – e^{-x} + C 

Example:
Evaluate ∫35ln⁡x dx\int_{3}^{5} \ln{x} \, dx .

  1. Choose u=ln⁡xu = \ln{x}  and dv=dxdv = dx .
    Therefore, du=1xdxdu = \frac{1}{x} dx  and v=xv = x .

  2. Using the integration by parts formula:

    ∫35ln⁡x dx=xln⁡x∣35−∫35x⋅1x dx\int_{3}^{5} \ln{x} \, dx = \left. x \ln{x} \right|_{3}^{5} – \int_{3}^{5} x \cdot \frac{1}{x} \, dx 
    ∫35ln⁡x dx=(xln⁡x−x)∣35\int_{3}^{5} \ln{x} \, dx = \left. (x \ln{x} – x) \right|_{3}^{5}

  3. Substitute the limits of integration:

    ∫35ln⁡x dx=(5ln⁡5−5)−(3ln⁡3−3)\int_{3}^{5} \ln{x} \, dx = \left( 5 \ln{5} – 5 \right) – \left( 3 \ln{3} – 3 \right) 
    =5ln⁡5−3ln⁡3−2= 5 \ln{5} – 3 \ln{3} – 2 

Products and (some) Quotients of Trigonometric Functions

For ∫sin⁡nxcos⁡mx dx\int \sin^n{x} \cos^m{x} \, dx , we have the following:

  1. nn  odd: Strip out one sine term and convert the rest to cosines using sin⁡2x=1−cos⁡2x\sin^2{x} = 1 – \cos^2{x} . Then use the substitution u=cos⁡xu = \cos{x} .
  2. mm  odd: Strip out one cosine term and convert the rest to sines using cos⁡2x=1−sin⁡2x\cos^2{x} = 1 – \sin^2{x} . Then use the substitution u=sin⁡xu = \sin{x} .
  3. nn  and mm  both odd: Use either method 1 or 2.
  4. nn  and mm  both even: Use double angle and/or half angle formulas to reduce the integral into a form that can be integrated.

For ∫tan⁡nxsec⁡mx dx\int \tan^n{x} \sec^m{x} \, dx , we have the following:

  1. nn  odd: Strip out one tangent and one secant term, and convert the rest to secants using tan⁡2x=sec⁡2x−1\tan^2{x} = \sec^2{x} – 1 . Then use the substitution u=sec⁡xu = \sec{x} .
  2. mm  even: Strip out two secant terms and convert the rest to tangents using sec⁡2x=1+tan⁡2x\sec^2{x} = 1 + \tan^2{x} . Then use the substitution u=tan⁡xu = \tan{x} .
  3. nn  odd and mm  even: Use either method 1 or 2.
  4. nn  even and mm  odd: Each integral will be dealt with differently.

Trigonometric Formulas

sin⁡(2x)=2sin⁡(x)cos⁡(x)\sin(2x) = 2 \sin(x) \cos(x) 
cos⁡2(x)=12(1+cos⁡(2x))\cos^2(x) = \frac{1}{2} (1 + \cos(2x)) 
sin⁡2(x)=12(1−cos⁡(2x))\sin^2(x) = \frac{1}{2} (1 – \cos(2x)) 

Example:

∫tan⁡3xsec⁡5x dx\int \tan^3{x} \sec^5{x} \, dx 

Rewrite and simplify:

∫tan⁡2xsec⁡4xtan⁡xsec⁡x dx\int \tan^2{x} \sec^4{x} \tan{x} \sec{x} \, dx 

Using the identity tan⁡2x=sec⁡2x−1\tan^2{x} = \sec^2{x} – 1 , we have:

∫(sec⁡2x−1)sec⁡4xtan⁡xsec⁡x dx\int (\sec^2{x} – 1) \sec^4{x} \tan{x} \sec{x} \, dx 

Substitute u=sec⁡xu = \sec{x} , then du=sec⁡xtan⁡x dxdu = \sec{x} \tan{x} \, dx :

∫(u2−1)u4 du\int (u^2 – 1) u^4 \, du 

Integrate term by term:

17u7−15u5+C\frac{1}{7} u^7 – \frac{1}{5} u^5 + C 

Substitute back u=sec⁡xu = \sec{x} :

17sec⁡7x−15sec⁡5x+C\frac{1}{7} \sec^7{x} – \frac{1}{5} \sec^5{x} + C 

Example:

∫sin⁡5xcos⁡3x dx\int \frac{\sin^5{x}}{\cos^3{x}} \, dx 

Rewrite and simplify:

∫sin⁡4x⋅sin⁡xcos⁡3x dx=∫(sin⁡2x)2⋅sin⁡xcos⁡3x dx\int \frac{\sin^4{x} \cdot \sin{x}}{\cos^3{x}} \, dx = \int \frac{(\sin^2{x})^2 \cdot \sin{x}}{\cos^3{x}} \, dx 

Using the identity sin⁡2x=1−cos⁡2x\sin^2{x} = 1 – \cos^2{x} , we have:

∫(1−cos⁡2x)2⋅sin⁡xcos⁡3x dx\int \frac{(1 – \cos^2{x})^2 \cdot \sin{x}}{\cos^3{x}} \, dx 

Substitute u=cos⁡xu = \cos{x} so that du=−sin⁡x dxdu = -\sin{x} \, dx :

−∫(1−u2)2u3 du-\int \frac{(1 – u^2)^2}{u^3} \, du 

Expand and integrate:

−∫(1−2u2+u4u3)du=−∫(1u3−2u2u3+u4u3)du-\int \left( \frac{1 – 2u^2 + u^4}{u^3} \right) du = -\int \left( \frac{1}{u^3} – \frac{2u^2}{u^3} + \frac{u^4}{u^3} \right) du 

Integrating each term:

−∫u−3 du+2∫u−1 du−∫u du-\int u^{-3} \, du + 2 \int u^{-1} \, du – \int u \, du 

Gives:

12u−2+2ln⁡∣u∣−12u2+C\frac{1}{2} u^{-2} + 2 \ln{|u|} – \frac{1}{2} u^2 + C 

Substitute back u=cos⁡xu = \cos{x} :

12sec⁡2x+2ln⁡∣cos⁡x∣−12cos⁡2x+C\frac{1}{2} \sec^2{x} + 2 \ln{| \cos{x} |} – \frac{1}{2} \cos^2{x} + C 

Trig Substitutions:

If the integral contains the following root, use the given substitution and formula to convert it into an integral involving trigonometric functions.

  1. For a2−b2x2\sqrt{a^2 – b^2x^2} use the substitution x=ab , and recall the identity cos⁡2θ=1−sin⁡2θ\cos^2{\theta} = 1 – \sin^2{\theta} .

  2. For b2x2−a2\sqrt{b^2x^2 – a^2} use the substitution x=ab , and recall the identity tan⁡2θ=sec⁡2θ−1\tan^2{\theta} = \sec^2{\theta} – 1 .

  3. For a2+b2x2\sqrt{a^2 + b^2x^2} use the substitution x=abtan⁡θx = \frac{a}{b} \tan{\theta} , and recall the identity sec⁡2θ=1+tan⁡2θ\sec^2{\theta} = 1 + \tan^2{\theta} .

Example:

∫16x24−9x2 dx\int \frac{16}{x^2 \sqrt{4 – 9x^2}} \, dx 

Substitute:

x=23sin⁡θ⇒dx=23cos⁡θ dθx = \frac{2}{3} \sin \theta \Rightarrow dx = \frac{2}{3} \cos \theta \, d\theta 

Rewrite the expression:

4−9x2=4−4sin⁡2θ=4cos⁡2θ=2∣cos⁡θ∣\sqrt{4 – 9x^2} = \sqrt{4 – 4 \sin^2 \theta} = \sqrt{4 \cos^2 \theta} = 2 |\cos \theta| 

Since this is an indefinite integral, we assume cos⁡θ\cos \theta  is positive and drop the absolute value bars:

4−9x2=2cos⁡θ\sqrt{4 – 9x^2} = 2 \cos \theta 

Thus,

∫16x24−9x2 dx=∫1649sin⁡2θ(2cos⁡θ)⋅23cos⁡θ dθ\int \frac{16}{x^2 \sqrt{4 – 9x^2}} \, dx = \int \frac{16}{\frac{4}{9} \sin^2 \theta (2 \cos \theta)} \cdot \frac{2}{3} \cos \theta \, d\theta

Simplify the integral:

=∫12sin⁡2θ dθ=12∫csc⁡2θ dθ= \int \frac{12}{\sin^2 \theta} \, d\theta = 12 \int \csc^2 \theta \, d\theta 
=−12cot⁡θ+C= -12 \cot \theta + C 

Using trigonometry to return to xx :

sin⁡θ=3x2⇒Triangle with opposite 3x, hypotenuse 2, adjacent 4−9x2\sin \theta = \frac{3x}{2} \Rightarrow \text{Triangle with opposite } 3x, \text{ hypotenuse } 2, \text{ adjacent } \sqrt{4 – 9x^2}

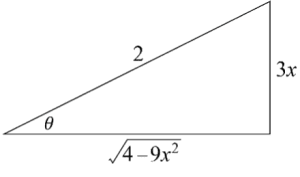
Trig Substitutions

From this triangle, we find:

cot⁡θ=4−9x23x\cot \theta = \frac{\sqrt{4 – 9x^2}}{3x}

Thus,

∫16x24−9x2 dx=−44−9x2x+C\int \frac{16}{x^2 \sqrt{4 – 9x^2}} \, dx = -\frac{4 \sqrt{4 – 9x^2}}{x} + C 

Partial Fractions:

When integrating an expression of the form:

∫P(x)Q(x) dx\int \frac{P(x)}{Q(x)} \, dx 

where the degree of P(x)P(x)  is smaller than the degree of Q(x)Q(x) :

  1. Factor the denominator Q(x)Q(x) as completely as possible.
  2. Find the partial fraction decomposition (P.F.D.) of the rational expression P(x)Q(x)\frac{P(x)}{Q(x)}.
  3. Integrate the partial fraction decomposition.

Integration Steps:

For each factor in the denominator, we create terms in the partial fraction decomposition according to the appropriate rules. This may involve distinct linear factors, repeated linear factors, irreducible quadratic factors, and so on. For example:

  • For distinct linear factors (x−a)(x – a) , we introduce terms of the form Ax−a\frac{A}{x – a}.
  • For repeated linear factors (x−a)n(x – a)^n , we introduce terms of the form A1x−a+A2(x−a)2+…+An(x−a)n\frac{A_1}{x – a} + \frac{A_2}{(x – a)^2} + \ldots + \frac{A_n}{(x – a)^n}.
  • For irreducible quadratic factors (ax2+bx+c)(ax^2 + bx + c) , we introduce terms of the form Ax+Bax2+bx+c\frac{Ax + B}{ax^2 + bx + c} .
Factor in Q(x)Q(x) Term in P.F.D.Factor in Q(x)Q(x) Term in P.F.D.
ax+bax + b Aax+b\frac{A}{ax + b}(ax+b)k(ax + b)^k A1ax+b+A2(ax+b)2+…+Ak(ax+b)k\frac{A_1}{ax + b} + \frac{A_2}{(ax + b)^2} + \ldots + \frac{A_k}{(ax + b)^k}
ax2+bx+cax^2 + bx + c Ax+Bax2+bx+c\frac{Ax + B}{ax^2 + bx + c}(ax2+bx+c)k(ax^2 + bx + c)^k A1x+B1ax2+bx+c+A2x+B2(ax2+bx+c)2+…+Akx+Bk(ax2+bx+c)k\frac{A_1x + B_1}{ax^2 + bx + c} + \frac{A_2x + B_2}{(ax^2 + bx + c)^2} + \ldots + \frac{A_kx + B_k}{(ax^2 + bx + c)^k}

Example:

Evaluate the integral:

∫7x2+13x(x−1)(x2+4)dx\int \frac{7x^2 + 13x}{(x – 1)(x^2 + 4)} dx 

Solution:

First, decompose the rational expression into partial fractions:

∫7x2+13x(x−1)(x2+4)dx=∫(4x−1+3x+16x2+4)dx\int \frac{7x^2 + 13x}{(x – 1)(x^2 + 4)} dx = \int \left( \frac{4}{x – 1} + \frac{3x + 16}{x^2 + 4} \right) dx 

Now split and integrate each term separately:

=∫4x−1dx+∫3xx2+4dx+∫16x2+4dx= \int \frac{4}{x – 1} dx + \int \frac{3x}{x^2 + 4} dx + \int \frac{16}{x^2 + 4} dx 

Integrating each term:

=4ln⁡∣x−1∣+32ln⁡(x2+4)+8tan⁡−1(x2)+C= 4 \ln|x – 1| + \frac{3}{2} \ln(x^2 + 4) + 8 \tan^{-1} \left( \frac{x}{2} \right) + C 

Partial Fraction Decomposition:

Given:

7x2+13x(x−1)(x2+4)=Ax−1+Bx+Cx2+4\frac{7x^2 + 13x}{(x – 1)(x^2 + 4)} = \frac{A}{x – 1} + \frac{Bx + C}{x^2 + 4}

Multiplying both sides by the common denominator:

7x2+13x=A(x2+4)+(Bx+C)(x−1)7x^2 + 13x = A(x^2 + 4) + (Bx + C)(x – 1) 

Expanding terms:

7x2+13x=(A+B)x2+(C−B)x+4A−C7x^2 + 13x = (A + B)x^2 + (C – B)x + 4A – C 

Equating coefficients yields the system of equations:

  • A+B=7A + B = 7 
  • C−B=13C – B = 13 
  • 4A−C=04A – C = 0 

Solving the system:

  • A=4A = 4 
  • B=3B = 3 
  • C=16C = 16 

This gives the partial fractions:

7x2+13x(x−1)(x2+4)=4x−1+3x+16x2+4\frac{7x^2 + 13x}{(x – 1)(x^2 + 4)} = \frac{4}{x – 1} + \frac{3x + 16}{x^2 + 4}

An alternate method that sometimes works to find constants involves setting the numerators equal in the previous example:

Given:

7x2+13x=A(x2+4)+(Bx+C)(x−1)7x^2 + 13x = A(x^2 + 4) + (Bx + C)(x – 1) 

Choose “nice” values of xx and plug them in. For example, if we let x=1x = 1 :

20=5A20 = 5A 

This yields:

A=4A = 4 

Note: This approach may not always be straightforward or work easily for every problem.

Applications of Integrals

Net Area:

 

∫abf(x) dx\int_{a}^{b} f(x) \, dx

 

represents the net area between

f(x)f(x)

 and the x-axis, where the area above the x-axis is positive and the area below the x-axis is negative.

Applications of Integrals Net Area: ∫ 𝑎 𝑏 𝑓 ( 𝑥 )   𝑑 𝑥 ∫ a b ​ f(x)dx represents the net area between 𝑓 ( 𝑥 ) f(x) and the x-axis, where the area above the x-axis is positive and the area below the x-axis is negative.

Area Between Curves:
The general formulas for finding the area between curves for two main cases are as follows:

  1. When y=f(x)y = f(x) : A=∫ab[upper function]−[lower function] dxA = \int_{a}^{b} [\text{upper function}] – [\text{lower function}] \, dx 
  2. When x=f(y)x = f(y) : A=∫cd[right function]−[left function] dyA = \int_{c}^{d} [\text{right function}] – [\text{left function}] \, dy 

If the curves intersect, the area of each portion must be calculated individually. Below are sketches and examples for a couple of possible scenarios and their corresponding formulas.

Area Between Curves: The general formulas for finding the area between curves for two main cases are as follows: When 𝑦 = 𝑓 ( 𝑥 ) y=f(x): 𝐴 = ∫ 𝑎 𝑏 [ upper function ] − [ lower function ]   𝑑 𝑥 A=∫ a b ​ [upper function]−[lower function]dx When 𝑥 = 𝑓 ( 𝑦 ) x=f(y): 𝐴 = ∫ 𝑐 𝑑 [ right function ] − [ left function ]   𝑑 𝑦 A=∫ c d ​ [right function]−[left function]dy If the curves intersect, the area of each portion must be calculated individually. Below are sketches and examples for a couple of possible scenarios and their corresponding formulas.

Volumes of Revolution:
To find the volume of a solid of revolution, the two main formulas are:

  1. V=∫A(x) dxV = \int A(x) \, dx 
  2. V=∫A(y) dyV = \int A(y) \, dy 

This approach depends on the axis about which the region is revolved. Here is some general information about each method of computation, accompanied by examples illustrating the application of these formulas.

Volumes of Revolution: The two main formulas are V=∫▒A(x) dx and V=∫▒A(y) dy. Here is some general information about each method of computing and some examples.
Volumes of Revolution: The two main formulas are V=∫▒A(x) dx and V=∫▒A(y) dy. Here is some general information about each method of computing and some examples.

Volumes of Revolution:
The two main formulas used to compute volumes of solids of revolution are:

V=∫A(x) dxandV=∫A(y) dy.V = \int A(x) \, dx \quad \text{and} \quad V = \int A(y) \, dy. 

The appropriate formula and axis of rotation depend on the method chosen and the axis about which the region is revolved.

Work:
For a force F(x)F(x)  moving an object in the interval a≤x≤ba \leq x \leq b , the work done is given by:

W=∫abF(x) dx.W = \int_{a}^{b} F(x) \, dx. 

Average Function Value:
The average value of a function f(x)f(x)  over the interval a≤x≤ba \leq x \leq b is:

favg=1b−a∫abf(x) dx.f_{\text{avg}} = \frac{1}{b – a} \int_{a}^{b} f(x) \, dx. 

Arc Length and Surface Area:
Arc length and surface area are often topics covered in Calculus II. The basic formulas for arc length (LL ) and surface area (SASA ) are as follows:

L=∫abds,SA=∫ab2πy ds(rotation about x-axis),L = \int_{a}^{b} ds, \quad SA = \int_{a}^{b} 2\pi y \, ds \quad (\text{rotation about } x\text{-axis}), 
SA=∫ab2πx ds(rotation about y-axis).SA = \int_{a}^{b} 2\pi x \, ds \quad (\text{rotation about } y\text{-axis}). 

The differential element dsds  depends on the form of the function being worked with:

  • For y=f(x)y = f(x) , a≤x≤ba \leq x \leq b : ds=1+(dydx)2dx.ds = \sqrt{1 + \left( \frac{dy}{dx} \right)^2} dx. 
  • For x=f(y)x = f(y) , a≤y≤ba \leq y \leq b : ds=1+(dxdy)2dy.ds = \sqrt{1 + \left( \frac{dx}{dy} \right)^2} dy. 
  • For parametric functions x=f(t)x = f(t)  and y=g(t)y = g(t) , a≤t≤ba \leq t \leq b : ds=(dxdt)2+(dydt)2dt.ds = \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2} dt. 
  • For polar coordinates r=f(θ)r = f(\theta) , a≤θ≤ba \leq \theta \leq b : ds=r2+(drdθ)2dθ.ds = \sqrt{r^2 + \left( \frac{dr}{d\theta} \right)^2} d\theta. 

In surface area computations, substitutions for xx  and yy  may be necessary depending on the chosen form of dsds .

Improper Integral:
An improper integral is characterized by infinite limits and/or discontinuous integrands. The integral is called convergent if the limit exists and has a finite value, and divergent if it does not exist or is infinite.

  1. Infinite Limit: ∫a∞f(x) dx=lim⁡t→∞∫atf(x) dx,∫−∞bf(x) dx=lim⁡t→−∞∫tbf(x) dx.\int_{a}^{\infty} f(x) \, dx = \lim_{t \to \infty} \int_{a}^{t} f(x) \, dx, \quad \int_{-\infty}^{b} f(x) \, dx = \lim_{t \to -\infty} \int_{t}^{b} f(x) \, dx. 
    ∫−∞∞f(x) dx=∫−∞cf(x) dx+∫c∞f(x) dxprovided both integrals are convergent.\int_{-\infty}^{\infty} f(x) \, dx = \int_{-\infty}^{c} f(x) \, dx + \int_{c}^{\infty} f(x) \, dx \quad \text{provided both integrals are convergent.} 
  2. Discontinuous Integrand:
    • Discontinuity at aa : ∫abf(x) dx=lim⁡t→a+∫tbf(x) dx.\int_{a}^{b} f(x) \, dx = \lim_{t \to a^{+}} \int_{t}^{b} f(x) \, dx. 
    • Discontinuity at bb : ∫abf(x) dx=lim⁡t→b−∫atf(x) dx.\int_{a}^{b} f(x) \, dx = \lim_{t \to b^{-}} \int_{a}^{t} f(x) \, dx. 
    • Discontinuity at a<c<ba < c < b : ∫abf(x) dx=∫acf(x) dx+∫cbf(x) dxprovided both integrals are convergent.\int_{a}^{b} f(x) \, dx = \int_{a}^{c} f(x) \, dx + \int_{c}^{b} f(x) \, dx \quad \text{provided both integrals are convergent.} 

Comparison Test for Improper Integrals:
If f(x)≥g(x)≥0f(x) \geq g(x) \geq 0  on [a,∞)[a, \infty) , then:

  1. If ∫a∞f(x) dx\int_{a}^{\infty} f(x) \, dx  converges, then ∫a∞g(x) dx\int_{a}^{\infty} g(x) \, dx  converges.
  2. If ∫a∞g(x) dx\int_{a}^{\infty} g(x) \, dx  diverges, then ∫a∞f(x) dx\int_{a}^{\infty} f(x) \, dx  diverges.

Useful Fact: For a>0a > 0 :

∫a∞1xpdxconverges if p>1 and diverges for p≤1.\int_{a}^{\infty} \frac{1}{x^p} dx \quad \text{converges if } p > 1 \text{ and diverges for } p \leq 1. 

Approximating Definite Integrals:
For a given interval ∫abf(x) dx\int_{a}^{b} f(x) \, dx  and a positive integer nn  (even for Simpson’s Rule), define:

Δx=b−an.\Delta x = \frac{b – a}{n}. 

Divide [a,b][a, b] into nn  subintervals [x0,x1],[x1,x2],…,[xn−1,xn][x_0, x_1], [x_1, x_2], \ldots, [x_{n-1}, x_n]  with x0=ax_0 = a  and xn=bx_n = b .

  • Midpoint Rule: ∫abf(x) dx≈Δx[f(x1∗)+f(x2∗)+⋯+f(xn∗)],xi∗ is the midpoint of [xi−1,xi].\int_{a}^{b} f(x) \, dx \approx \Delta x \left[ f(x_1^{*}) + f(x_2^{*}) + \cdots + f(x_n^{*}) \right], \quad x_i^{*} \text{ is the midpoint of } [x_{i-1}, x_i]. 
  • Trapezoid Rule: ∫abf(x) dx≈Δx2[f(x0)+2f(x1)+2f(x2)+⋯+2f(xn−1)+f(xn)].\int_{a}^{b} f(x) \, dx \approx \frac{\Delta x}{2} \left[ f(x_0) + 2f(x_1) + 2f(x_2) + \cdots + 2f(x_{n-1}) + f(x_n) \right]. 
  • Simpson’s Rule: ∫abf(x) dx≈Δx3[f(x0)+4f(x1)+2f(x2)+⋯+2f(xn−2)+4f(xn−1)+f(xn)].\int_{a}^{b} f(x) \, dx \approx \frac{\Delta x}{3} \left[ f(x_0) + 4f(x_1) + 2f(x_2) + \cdots + 2f(x_{n-2}) + 4f(x_{n-1}) + f(x_n) \right]. 
 

More Sly academy Content

Tonsillitis
Disease

Tonsillitis – Everything you need to know

Tonsillitis Below is a comprehensive, structured report on Tonsillitis covering all essential aspects. This report is based on current medical literature and guidelines from reputable

Open »
March 11, 2025 No Comments