6.1 Simple Harmonic Motion, Springs, and Pendulums
Understanding Simple Harmonic Motion (SHM)
Simple Harmonic Motion (SHM) is a fascinating concept in physics that underpins many natural and man-made systems. It describes a type of periodic motion where an object oscillates about an equilibrium position with a constant amplitude and frequency. This motion is governed by a restoring force that is directly proportional to the displacement from the equilibrium position and acts in the opposite direction. Let’s dive into the world of SHM and explore its applications, mathematical representations, and energy dynamics.
Key Characteristics of SHM
Restoring Force and Displacement:
The restoring force in SHM is proportional to the displacement and follows Hooke’s Law: Here, is the spring constant, and is the displacement.
Equation of Motion:
The displacement as a function of time is given by: Where:
: Amplitude
: Angular frequency
: Phase angle
Frequency and Period:
Angular frequency and period are related by: Where is the period, and is the frequency.
Velocity and Acceleration:
Velocity and acceleration in SHM are derived from displacement:
Maximum velocity occurs at the equilibrium position, while maximum acceleration occurs at maximum displacement.
Energy in SHM:
SHM systems conserve mechanical energy, with total energy being the sum of kinetic energy and potential energy:
Kinetic energy:
Potential energy:
Applications and Examples of SHM
SHM appears in numerous physical systems. Some of the most common examples include:
Mass-Spring Systems: When a mass is attached to a spring and displaced, it oscillates due to the restoring force provided by the spring.
Period of oscillation: Where is the mass and is the spring constant.
Pendulums: A simple pendulum exhibits SHM when displaced from equilibrium. Its period is given by: Where is the length of the pendulum, and is the acceleration due to gravity.
Electric Circuits: Oscillations in LC circuits are analogous to SHM, with charge and current oscillating sinusoidally.
Musical Instruments: Vibrations of strings and air columns produce harmonic motion, creating musical notes.
The Role of Calculus in SHM
SHM provides an excellent opportunity to apply calculus concepts. By taking derivatives, we can derive relationships between displacement, velocity, and acceleration:
Displacement:
Velocity (first derivative of displacement):
Acceleration (second derivative of displacement):
The sinusoidal nature of these equations reveals the interplay between these quantities and highlights key points such as zero crossings, maxima, and minima.
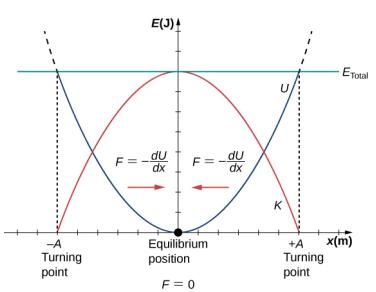
Energy Analysis in SHM
Energy in SHM alternates between kinetic and potential forms:
At Maximum Displacement:
Potential energy is maximum:
Kinetic energy is zero:
At Equilibrium Position:
Kinetic energy is maximum:
Potential energy is zero:
The total mechanical energy remains constant throughout the motion:
Graphical Representation:
Graphs of energy in SHM show potential and kinetic energy as sinusoidal functions that are out of phase with each other.
Differential Equation for SHM
The equation governing SHM arises from Newton’s Second Law: Rearranging gives: This second-order differential equation is the hallmark of SHM and can describe any oscillatory system with a linear restoring force.
Analyzing Springs and Pendulums
Mass-Spring Systems
Equation of motion:
Period:
Simple Pendulums
Equation of motion:
Period:
Real-World Factors in SHM
While SHM is an idealized model, real-world oscillatory systems are affected by:
Damping:
Frictional forces reduce amplitude over time, leading to damped oscillations.
External Forces:
External periodic forces can cause resonance, amplifying oscillations when the driving frequency matches the natural frequency.
Nonlinearities:
Systems with non-linear restoring forces deviate from SHM, resulting in more complex motions.
Conclusion
Simple Harmonic Motion is a cornerstone of physics, providing insights into oscillatory systems and energy dynamics. Its applications extend from engineering to music, making it a vital concept for both theoretical understanding and practical use. Mastering SHM lays the groundwork for exploring more complex motions and systems in physics. Embrace the elegance of SHM and apply its principles to uncover the secrets of periodic motion.
50 Highly Trending FAQs About Simple Harmonic Motion, Springs, and Pendulums
1. What is Simple Harmonic Motion (SHM)? Simple Harmonic Motion (SHM) is a type of oscillatory motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. It is mathematically described by sinusoidal functions.
2. What is the formula for SHM? The general equation for SHM is:
where is the restoring force, is the spring constant, and is the displacement.
3. What is the difference between oscillatory motion and SHM? Oscillatory motion includes all periodic motions, while SHM is a specific type of oscillation with a linear restoring force proportional to displacement.
4. What are examples of SHM in daily life? Examples include:
The motion of a pendulum (for small angles)
Vibrating guitar strings
Mass-spring systems
Oscillations in quartz crystals in watches
5. How do you determine the period of SHM? The period is the time for one complete cycle of oscillation and is given by:
6. What is the relationship between period and frequency in SHM? Frequency is the reciprocal of the period:
7. What is the phase in SHM? Phase represents the state of motion of the oscillating system at any given time. It is expressed as an angle in radians or degrees.
8. What is amplitude in SHM? Amplitude is the maximum displacement of the system from its equilibrium position. It indicates the energy of the motion.
9. What is angular frequency in SHM? Angular frequency is the rate of change of the phase angle and is given by:
10. What is a spring constant? The spring constant is a measure of a spring’s stiffness. It determines the force required to stretch or compress the spring by a unit distance.
11. How does mass affect the period of a spring? The period of a spring-mass system increases with the mass :
12. What is a simple pendulum? A simple pendulum consists of a mass (bob) attached to a string, swinging back and forth under the influence of gravity. Its motion approximates SHM for small angular displacements.
13. What is the formula for the period of a pendulum? The period of a simple pendulum is:
where is the length of the string and is the acceleration due to gravity.
14. What are damped oscillations? Damped oscillations occur when the amplitude decreases over time due to resistive forces like friction or air resistance.
15. What is the difference between overdamped, underdamped, and critically damped motion?
Underdamped: Oscillations occur with gradually decreasing amplitude.
Overdamped: The system returns to equilibrium without oscillating.
Critically damped: The system returns to equilibrium as quickly as possible without oscillating.
16. How does damping affect SHM? Damping reduces the amplitude and energy of SHM over time, altering the motion’s duration and frequency.
17. What is resonance in oscillations? Resonance occurs when a system is driven at its natural frequency, resulting in maximum amplitude. Examples include breaking a glass with sound and tuning forks.
18. What are free and forced oscillations?
Free oscillations: Occur without external forces, relying solely on initial energy.
Forced oscillations: Involve an external periodic force driving the system.
19. How is energy distributed in SHM? In SHM, energy alternates between kinetic and potential forms, with the total energy remaining constant (in the absence of damping).
20. What is the total energy in a spring system? The total energy is:
where is the amplitude and is the spring constant.
21. How does gravity affect a pendulum? Gravity provides the restoring force for a pendulum, influencing its period and motion. The period decreases on planets with higher gravitational acceleration.
22. What are coupled pendulums? Coupled pendulums are two or more pendulums connected so that energy can transfer between them, leading to phenomena like synchronization.
23. What is the natural frequency of a spring? The natural frequency is:
24. What is anharmonic motion? Anharmonic motion deviates from SHM due to non-linear restoring forces, resulting in complex oscillations.
25. How does length affect a pendulum’s period? The period of a pendulum increases with the square root of its length:
26. What are physical pendulums? Physical pendulums involve rigid bodies oscillating about a pivot point. Their period depends on their moment of inertia and the distance from the pivot to the center of mass.
27. What is the difference between a simple and a physical pendulum? A simple pendulum assumes a point mass and massless string, while a physical pendulum considers the distribution of mass.
28. How is SHM related to circular motion? SHM can be visualized as the projection of uniform circular motion onto one axis, sharing the same mathematical description.
29. What is a torsional pendulum? A torsional pendulum oscillates by twisting about its axis. Examples include the balance wheel in watches and torsion springs.
30. What is the spring-mass system? The spring-mass system involves a mass attached to a spring, oscillating due to restoring forces. It is a classic example of SHM.
31. How is SHM used in clocks? SHM underpins the mechanism of pendulum clocks and quartz oscillators in modern clocks, providing precise timekeeping.
32. What is the Q-factor in oscillations? The Q-factor measures the sharpness of resonance and energy retention in oscillations. Higher Q-factors indicate lower energy loss.
33. How does air resistance affect a pendulum? Air resistance introduces damping, reducing the amplitude and slightly increasing the period over time.
34. What are driven oscillations? Driven oscillations occur when an external force continuously drives the system, often at a frequency different from its natural frequency.
35. What is the role of elasticity in springs? Elasticity determines the ability of a spring to store and release energy. The spring constant quantifies this property.
36. How are pendulums used in seismology? Pendulums are used in seismometers to detect ground motion during earthquakes, as their oscillations record seismic waves.
37. What is the effect of amplitude on period in SHM? In ideal SHM, the period is independent of amplitude. For large amplitudes in pendulums, deviations occur due to non-linear effects.
38. How does temperature affect springs? Temperature changes can alter a spring’s elasticity, affecting its spring constant and oscillatory behavior.
39. What is the energy transfer in a coupled spring system? Energy oscillates between the springs and masses, leading to phenomena like normal modes and energy beats.
40. What is the restoring force in SHM? The restoring force is the force that pulls the system back toward equilibrium, proportional to the displacement in SHM.
41. How are pendulums used in engineering? Pendulums are used in structural engineering to dampen vibrations in skyscrapers and bridges, such as tuned mass dampers.
42. What is the significance of the equilibrium position in SHM? The equilibrium position is where the net force on the system is zero. It is the central point about which oscillations occur.
43. How do frictional forces affect SHM? Frictional forces introduce damping, causing the system to lose energy and eventually stop oscillating.
44. What are standing waves in springs? Standing waves form in springs when waves traveling in opposite directions interfere, creating nodes and antinodes.
45. What are real-life applications of SHM? Applications include:
Timekeeping devices
Musical instruments
Suspension systems in vehicles
Seismic monitoring
46. What is the effect of gravity on SHM in space? In microgravity, pendulums do not exhibit SHM, but spring-mass systems remain unaffected as their motion depends on elastic forces.
47. What is the relationship between potential and kinetic energy in SHM? In SHM, energy alternates between potential and kinetic forms, with total energy remaining constant.
48. How do you calculate displacement in SHM? Displacement is given by:
where is amplitude, is angular frequency, and is the phase constant.
49. What are the limitations of the small-angle approximation in pendulums? The small-angle approximation is valid only for angles less than about 15 degrees. Beyond this, the motion deviates from SHM.
50. How are oscillations in springs and pendulums studied in physics? These systems are studied using mathematical models, experiments, and simulations to understand principles of mechanics, energy transfer, and resonance.







