SAT Math Overview
Welcome to another SAT Math guide! The Problem Solving & Data Analysis portion of the SAT Math exam makes up 17/58 questions, or about 30% of the math section. You should be able to change/convert to common units, understand percentages, read data from charts, graphs, or tables, and determine whether data is linear or exponential. Before we jump into the practice questions, let’s break down the skills you need to be successful. You got this!
Main Problem Solving & Data Analysis Topic Areas
College Board has provided a list of skills that may be tested under “Problem Solving & Data Analysis.” We’ve put this list of skills into three groups for you to focus on! Don’t worry, we’ll take you through all of these. Here is a checklist for you to work off of:
Group 1: Ratio, Proportion, Units, and Percentage
- These skills are usually based on comparing two numbers and predicting unknown values. Group 2: Interpreting Relationships Presented in Scatterplots, Graphs, Tables, and Equations
- In these types of questions, you will need to look at how two variables interact and change. These relationships can be modeled as linear, quadratic, or exponential graphs and equations.
- This group includes table data, scatterplots, and linear and exponential growth. Group 3: More Data and Statistics
- These questions may ask you to interpret the provided data, sometimes by identifying key values or calculating probabilities.
- This group includes data inferences, statistical distributions, and data collection and conclusions.
Ratio, Proportion, Units, and Percentage
Ratios and proportions are usually based on comparing two numbers. These questions can become tricky if you mix up numbers.
What You Need to Know: Ratio, Proportion, Units, and Percentage
This group of skills focuses on comparing numbers, predicting unknown values, and understanding proportions, units, and percentages.
Understanding Ratios, Proportions, Units, and Percentages
1.Ratios compare two different values or parts, such as comparing the number of apples to oranges.
2.Proportions represent one part of a whole, such as three stars out of five.
3.Percentages represent a part of 100, often used to describe proportions or changes in data.
Key Concepts and Applications
•Ratio and Proportion: You should be able to apply ratios and proportions to word problems, ensuring that ratios are simplified and proportions are correctly interpreted.
•Unit Conversion: Being able to convert between different units, such as inches to feet or grams to kilograms, is essential.
•Percentage Calculations: Understanding how to calculate percentages, especially percentage changes, is a crucial skill.
For the first group of skills, you should be able to:
- Identify the difference between ratios, proportions, and percents.- – A ratio is a comparison of two different values, or parts. 🍎🍎🍎🍎:🍊🍊🍊- – A proportion represents one part of a whole. ★★★☆☆- – A percent is a part of 100.
- Apply the properties of proportion to word problems.
- Manipulate fractions and decimals.
- Convert to common units and between percentages, fractions, and decimals.
- Simply ratios. Ratios are always simplified.
- Calculate the change in percentage. Change in % = the difference in percentages / the total * 100
Applying Your Knowledge: Ratio, Proportion, Units, and Percentage
Unit Conversion Practice
Some common conversions are between measures of distance, such as from yards to inches. You can create a conversion table like the one below to work through the problem.
| 4 yards | 3 feet | 12 inches | = | 144 inches |
| 1 yard | 1 foot |
Let’s practice converting 4 yards into inches. Here are the steps you should follow:
- First, place the given, initial value on the very left! This value is 4 yards.
- Next, we can use the identity property by multiplying that initial value by a fraction equal to 1. This allows the units to cancel out. For instance, since 3 feet equals 1 yard, we can write the fraction as 3 feet / 1 yard.
- Once we multiply 4 yards x (3 feet / 1 yard), we get 12 feet. Notice how the unit, “yards,” got canceled out. Make sure to place the value with the original unit (yards) in the denominator so that the unit cancels and we’re left with the new unit (feet). 🚶♂️
- You can then repeat this until you get the value in your desired unit. To convert 4 yards to inches, we did that process twice—by multiplying by two fractions equivalent to one—to get the final answer of 144 inches.
Percentage Practice
To calculate a percentage, we divide the value of the part by the total value and multiply by 100.
Let’s say there were 32 students in a class and 12 of them were on a field trip. We were then asked to calculate the percentage of students that were PRESENT.
- We can begin by calculating the number of students present: 32-12 = 20 students in class. This tells us that a part of the whole class, 20 students out of 32, were present.
- Then, we take that part and divide it by the total number of students: 20/32 = 0.625.
- After multiplying by 100, we find that 62.5% of students were in class that day.
Interpreting Relationships Presented in Scatterplots, Graphs, Tables, and Equations
In these types of questions, you will need to look at how two variables interact and change. These relationships can be modeled as linear, quadratic, or exponential graphs and equations.
What You Need to Know: Scatterplots, Graphs, Tables, and Equations
For the second group of skills, you should be able to:
- Interpret data from charts, graphs, or tables.- – Find and interpret a line of best fit to given data.- – Place data within given contexts of world problems
- Determine whether a function is linear or exponential:- – If there is a common difference in data values, the relationship is linear. Linear relationships can be modeled by y=mx + b. ↗- – If there is a common productbetween data, the relationship is exponential. Exponential relationships can be modeled by y=a(b)x ⤴
Applying Your Knowledge: Scatterplots, Graphs, Tables, and Equations
Linear vs. Exponential Functions
One tip for finding a line of best fit is to draw a line that has approximately an equal number of points above and below the line. This doesn’t have to be exact, but should serve as a good indicator of any patterns in the data. Let’s also look at finding differences in data values.
Table A:

If you look at the changes in outputs and inputs of Table A, you may notice that each Y value increases by 3 to make the next Y value. Since there is a common difference, where 3 is being added each time, we can conclude that this is a linear relationship.
Table B:

If you take a look at Table B, you may find that adding and subtracting a constant value does not provide the next output value. Instead, there is a common product between the values. You may have noticed that multiplying a Y value by 2 provides the next Y value. In this case, 2 is the common product, and Table B is modeling an exponential relationship.
More Data and Statistics
These questions may ask you to interpret the provided data, sometimes by identifying key values or calculating probabilities.
What You Need to Know: More Data and Statistics
Congrats, you made it to the last group of skills! For the third and final group of skills, you should be able to:
- Answer questions that involve the measures of central tendency:- – The mean number of a data set is the mathematical average.- – The median number of a data set in order from least to greatest is the middle number.- – The mode of a data set is the most commonly occurring number.
- Use data to calculate probability:- – If event A and event B must occur, multiply the individual probabilities together.- – If event A or event B can occur, add the individual probabilities together.
- Understand sampling procedures in statistics:- – Samples must be randomly chosen and representative of the whole population in order to generalize the conclusions to the whole population.- – Samples must be randomly assigned to treatment groups for an experiment if determining cause and effect.
Applying Your Knowledge: More Data and Statistics
Measures of Central Tendency Practice
Take a look at this data set: 3, 6, 7, 9, 1, 22, 4, 6, 8.
- To find the mean, we can add up all the numbers and divide by the number of values in the set (9). Since 3 + 6 + 7 + 9 + 1 + 22 + 4 + 6 + 8 = 66, the mean equals 66 / 9 = 7.33.
- To find the median, we first have to place the data set in order: 1, 3, 4, 6, 6, 7, 8, 9, 22. Since there are 9 values in the set and the median is the middle value, the fifth value in this set is the median: 6.
- The mode is just the most occurring value. Since 6 occurs twice in this data set, and all of the other numbers occur only once, 6 is the mode.
Probability Practice
Let’s review some probability too. Imagine a jar of 20 cookies, where 12 are chocolate chip, 5 are peanut butter, and 3 are Snickerdoodles.
- If you were asked the probability of randomly choosing a peanut butter or Snickerdoodle cookie, you would have to add the probabilities of choosing either together.
- Since the probability of choosing peanut butter is 5/20 and choosing Snickerdoodle is 3/20, we calculate that the probability of choosing either is 5/20 + 3/20 = 8/20. 🎲 You may also be asked to calculate the probability of event A and event B happening. In this case, you would multiply the two probabilities. For instance, imagine you rolled two dies and wanted to calculate the probability that both would provide a number less than 3.
- The probability of getting a number less than 3 on dice A is 2/6.
- The probability of getting a number less than 3 on dice B is also 2/6.
- The probability of both events occurring can be found by multiplying the separate probabilities together. Therefore, the probability that both would provide a number less than 3 equals 2/6 * 2/6 = 4/36.
SAT Math Sample Questions + Explanations
SAT Math Questions 1-3: Line of Best Fit Practice
The following graph will be used for questions 1-3. These three questions fit under the second group of skills we outlined above! Let’s take a look and go over some of its key points. You can open the image in a new tab to see it in a larger size! ↘️

Image Courtesy of College Board’s SAT Student Guide
One of the main things to note about this graph is that the line is a line of best fit and is only meant to represent a pattern. The dots are the real data points that represent individuals and their characteristics.
Question 1: Line of Best Fit
- This question is considered “easy” in difficulty. Analyzing the line of best fit and comparing it to individual data points is important for solving this question.
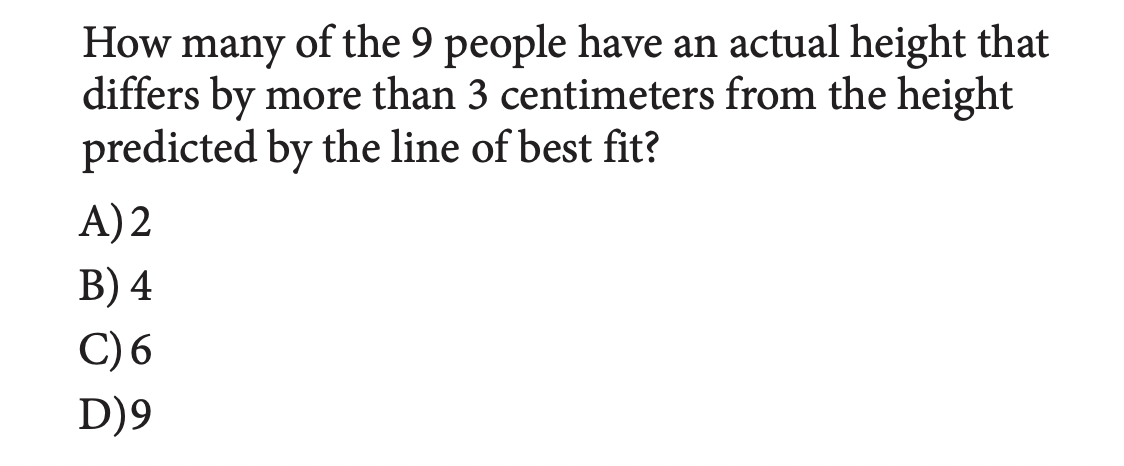
Image Courtesy of College Board’s SAT Student Guide
The correct answer is B.
The individual’s height, given by the y value of the data point, must be at least 3 centimeters away from the height predicted by the line of best fit. There are four individuals with a height that is at least 3 centimeters greater or less than their predicted height: the people with metacarpal bones of 4, 4.3, 4.8, and 4.9 cm.
Question 2: Analyzing Slope
- This question is considered “easy” in difficulty. You will need to analyze the slope in context.

Image Courtesy of College Board’s SAT Student Guide
The correct answer is A.
Slope can be thought of as the change in the y value for each change in the x value. In this situation, the height is represented on the y-axis, and the length of the metacarpal bone is represented on the x-axis, so the slope must represent a change in height based on a change in the length of the metacarpal bone.
This eliminates answer choices B and D, which state the opposite. Answer choice C can also be eliminated because the slope never identifies a single value when the input is 0 – that is actually the y-intercept! Therefore, choice A is the only correct answer.
Question 3 – Estimating with the Line of Best Fit
- This question is considered “easy”. You will need to use the line of best fit to make an estimate.

Image Courtesy of College Board’s SAT Student Guide
The correct answer is C.
For this question, you’ve already been given the input, or the x value, which is 4.45 cm. You can then find this value on the x-axis as being between the line that marks 4.4 cm and the line that marks 4.5 cm.
If you draw a straight vertical line where x=4.45 and find the point of intersection with the line of best fit, you will find that the line of best fit predicts that an individual with a metacarpal bone 4.45 cm long is predicted to be 170 cm in height. Don’t be afraid to mark up your test paper!
SAT Math Questions 4: Unit Conversion Practice
- The following example is considered “medium” in difficulty. Conversion between megabytes and gigabytes and converting between hours, minutes, and seconds is necessary for success in this problem. This fits under the first group of skills we outlined. Remember the conversion from yards to inches?

Image Courtesy of College Board’s SAT Practice Problems
The correct answer is B.
Before we start our dimensional analysis, lets review some important facts about the scenario: 1 hour = 3600 seconds, 1 gigabit = 1024 megabits, and 1 image = 11.2 gigabits.
| 3 megabits | 1 gigabit | 1 image | 3600 seconds | 11 hours | = | 10.3585 images |
| 1 second | 1024 megabits | 11.2 gigabit | 1 hour |
Your conversion table should be set up similarly to this! The key to solving these types of questions is to make sure your original values all cancel out as you multiply the conversion factors to finally reach the intended units.
Using the table, we were able to figure out that approximately 10 images per day (rounded down) can be sent daily.
To solidify your understanding, let’s explore some practice questions that integrate these concepts.
Practice Question 1: Line of Best Fit
Given a scatterplot with a line of best fit, identify which point deviates most from the line.
Solution:
Identify the data point with the largest vertical distance from the line of best fit. This point represents the greatest deviation.
Practice Question 2: Slope Interpretation
A graph shows the relationship between the length of metacarpal bones and height. What does the slope of the line of best fit represent?
Solution:
The slope represents the rate of change in height per unit change in the length of metacarpal bones.
Practice Question 3: Unit Conversion
Convert the rate of data transfer from megabits per second to gigabytes per hour, given that 1 gigabyte = 1024 megabytes.
Solution:
Use dimensional analysis to convert the units systematically, ensuring accuracy by canceling out the appropriate units during multiplication.






