Q.1. Find the volume of the solid formed by revolving the region bounded by the graph of the equation the x - axis and the y - axis about the x - axis.

Recall that the volume of a solid formed when a curve is revolved about the x - axis is given by:
Taking the constant (π) outside of the integral, we get:
Here, f(x) is the given function, which is And since we are finding the volume of the solid formed when this curve is revolved about the x - axis from x = 0 to x = 2, the integral becomes:
This simplifies to:
We now integrate:
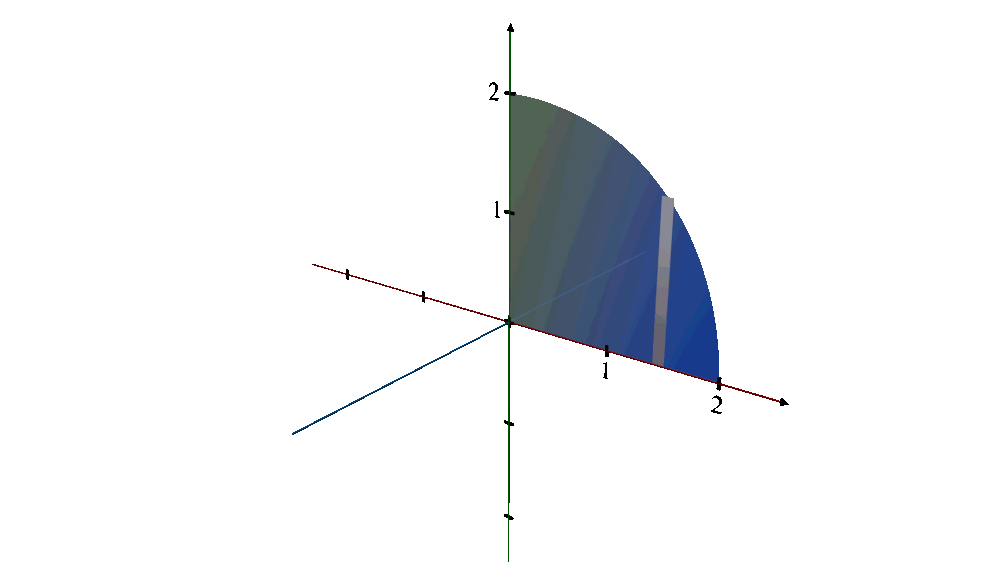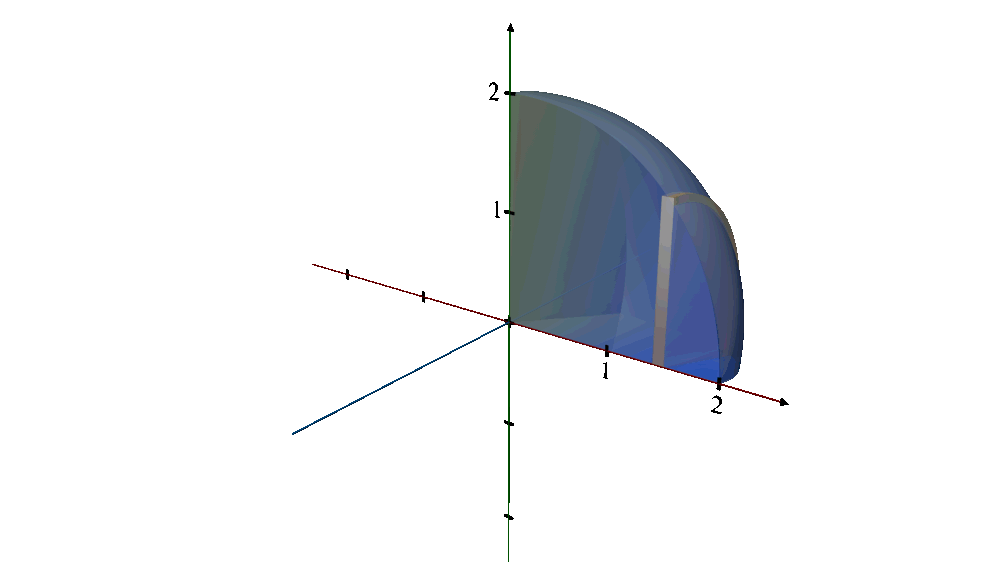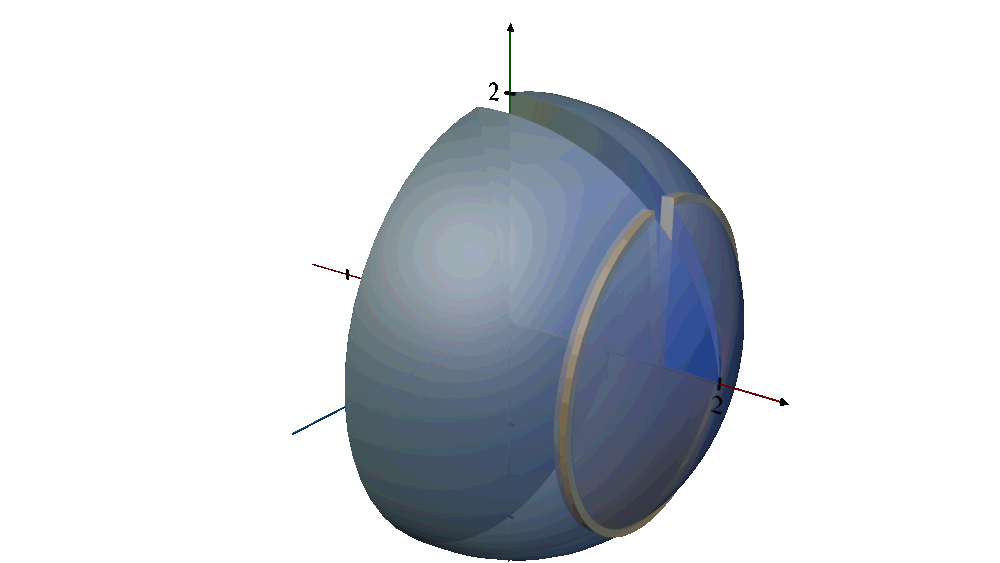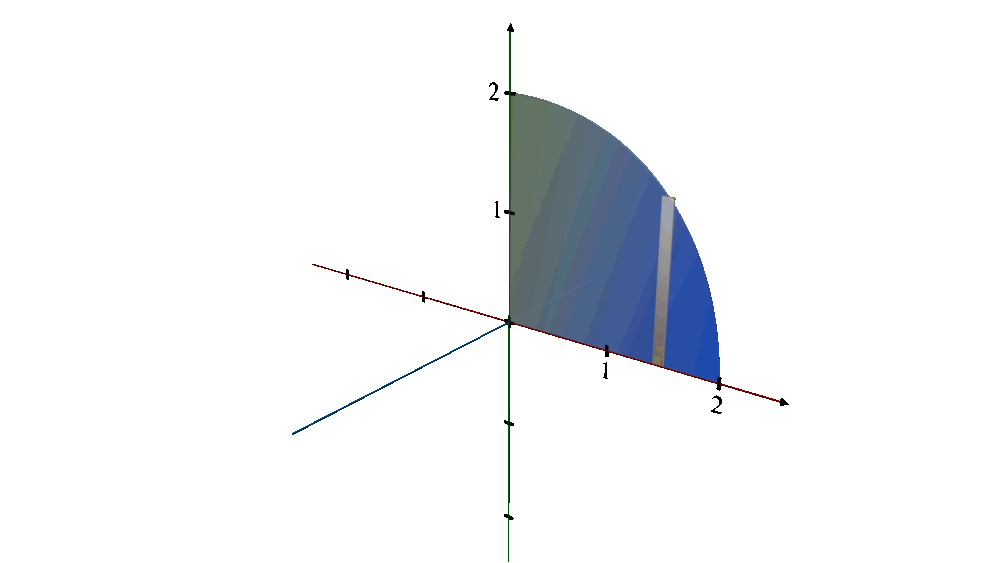
Shape Description:
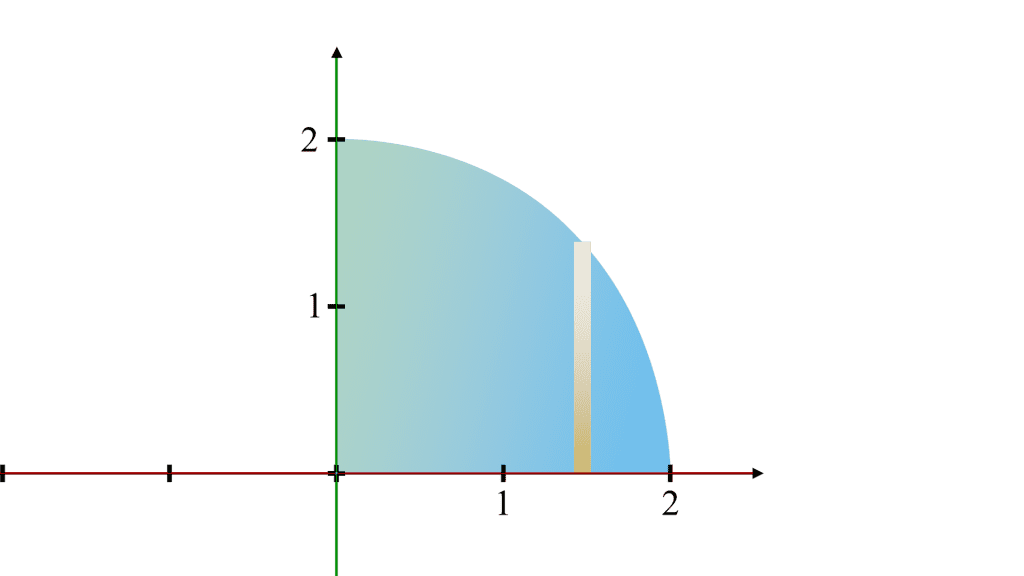
1.The original curve,
describes a quarter-circle with a radius of 2 centered at the origin, covering the domain from
x = 0 to x = 2. When this quarter-circle is revolved around the
x - axis, it generates a hemisphere.
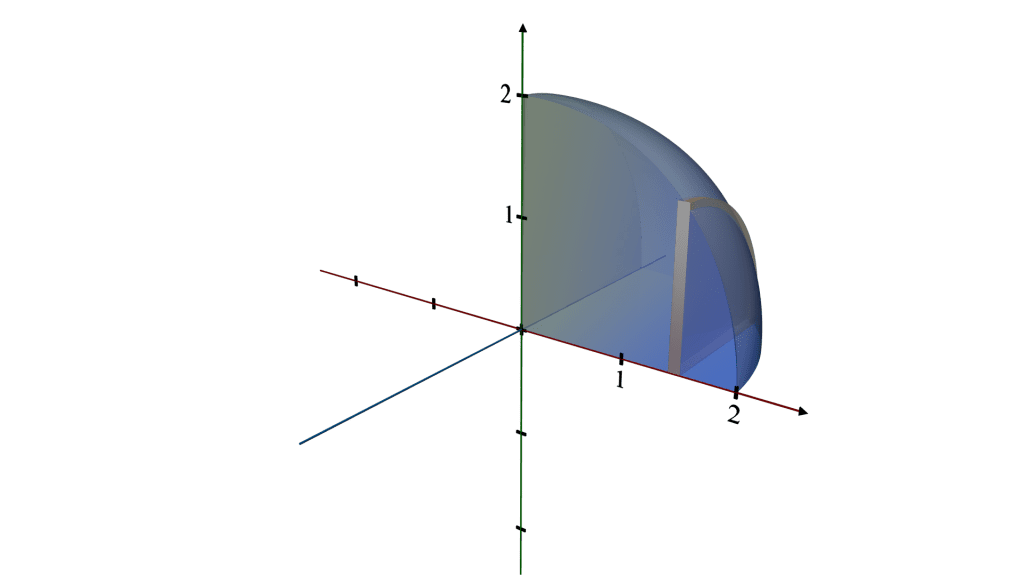
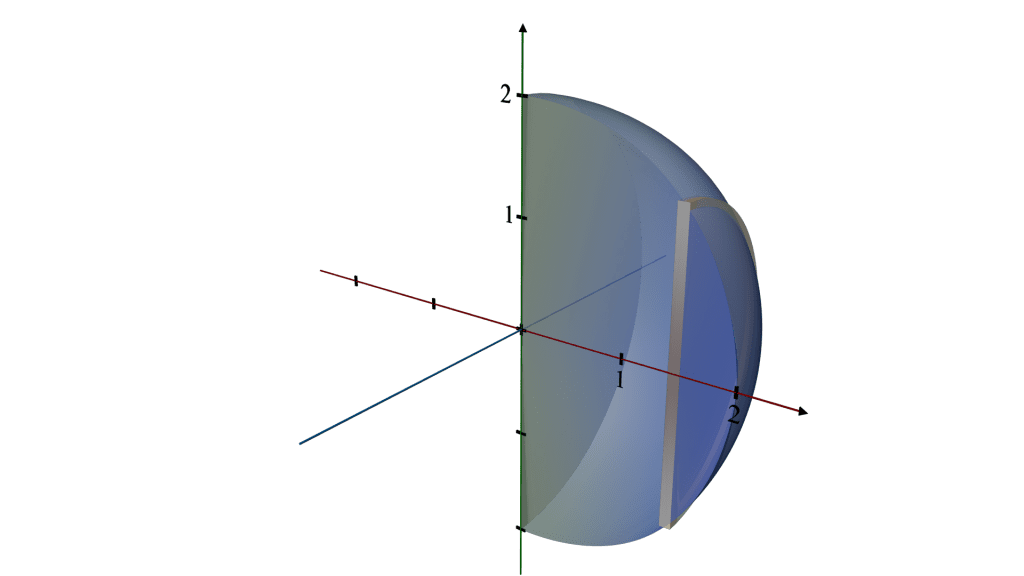
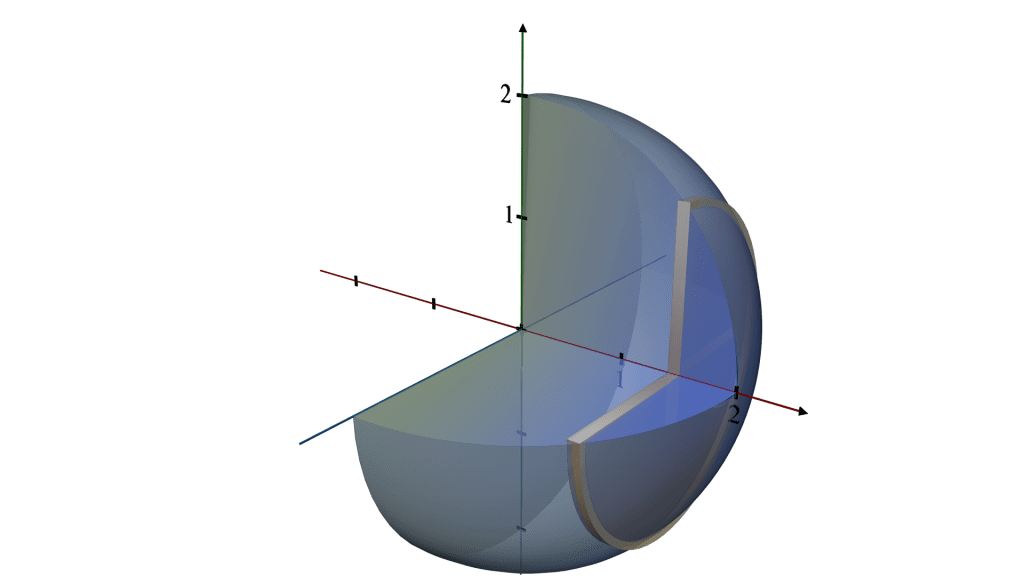

Visualizing the 3D Object:
Imagine taking a quarter-circle cutout, and as you spin it around the x-axis (a line running vertically from the edge to the radius), the edges trace out the surface of a hemisphere.
Every point on the rim of the quarter-circle moves in a circular path around the x-axis, contributing to the hemispherical shape.
The result is a solid that looks like half a ball where every point on the surface is equidistant from the center, located at the origin (0,0).
Q. 2. Find the volume of the solid formed by revolving the region bounded by the graph of the equation y = x2 , the x-axis and the line x = 1, about the x-axis.
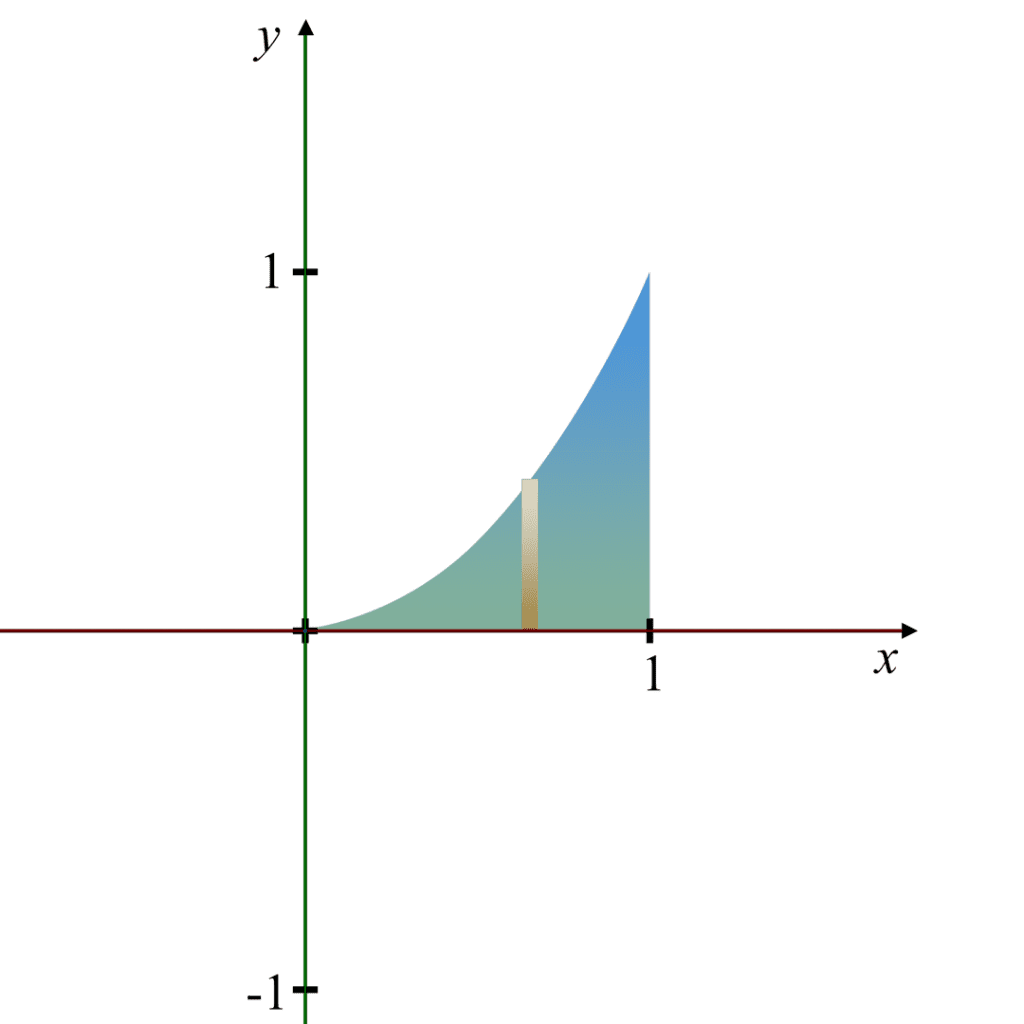
Recall that the volume of a solid formed when a curve is revolved about the x - axis is given by
Taking the constant (π) outside of the integral, we get:
Here, f(x) is the given function, which is y = x2. And since we are finding the volume of the solid formed when this curve is revolved about the x-axis from x = 0 to x = 1, the integral becomes:
This becomes:
Integrating, we get:
Shape Description:
1. Region: The region is bounded by the parabola y = x2, the x-axis (i.e., y = 0), and the vertical line x = 1.
2. Revolution: When this region is revolved around the x -axis, it forms a 3D solid.
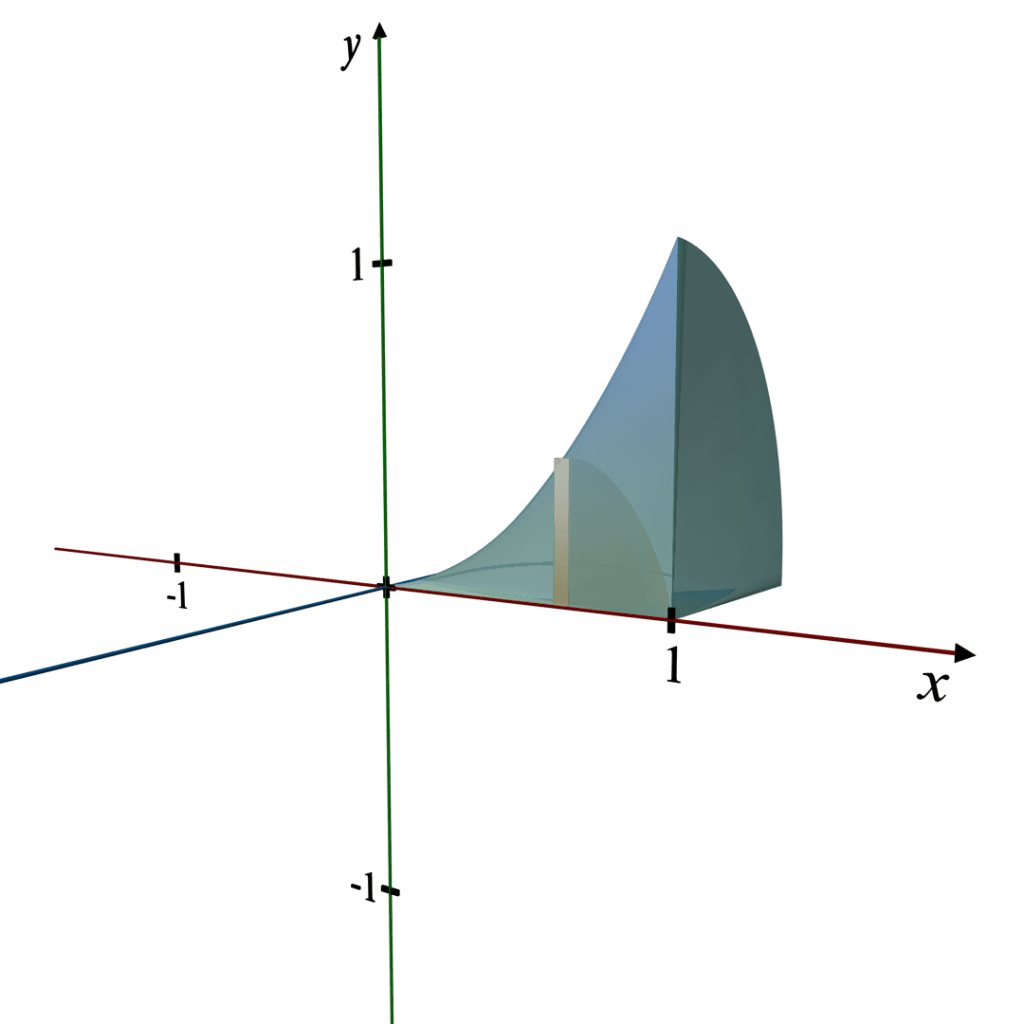
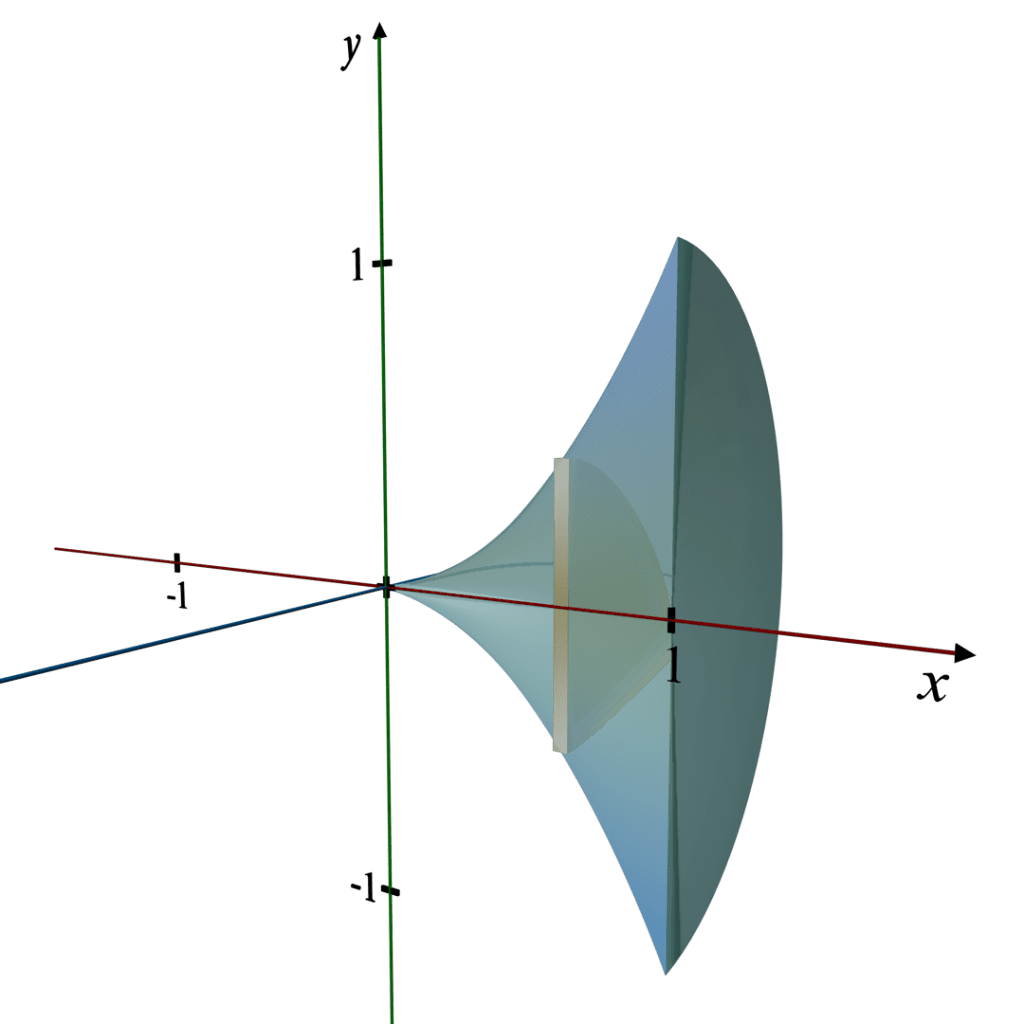
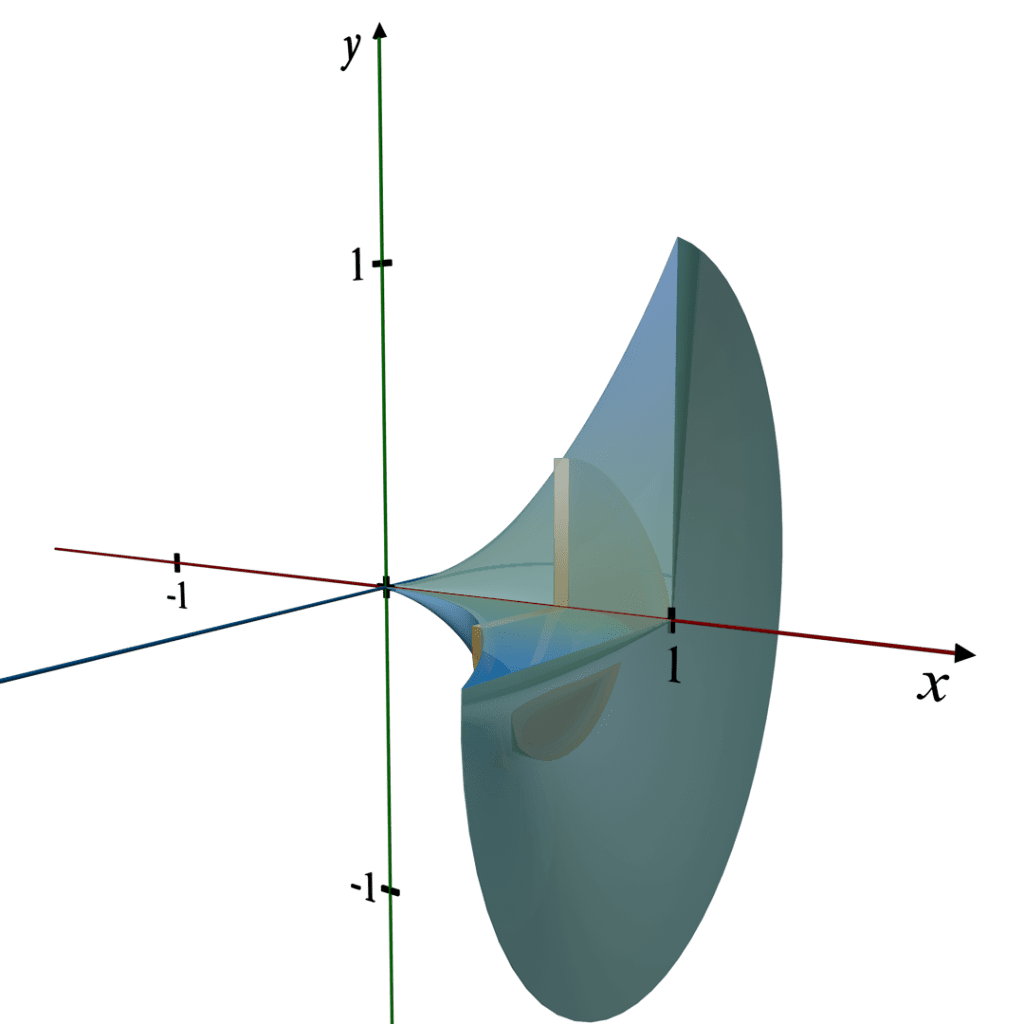
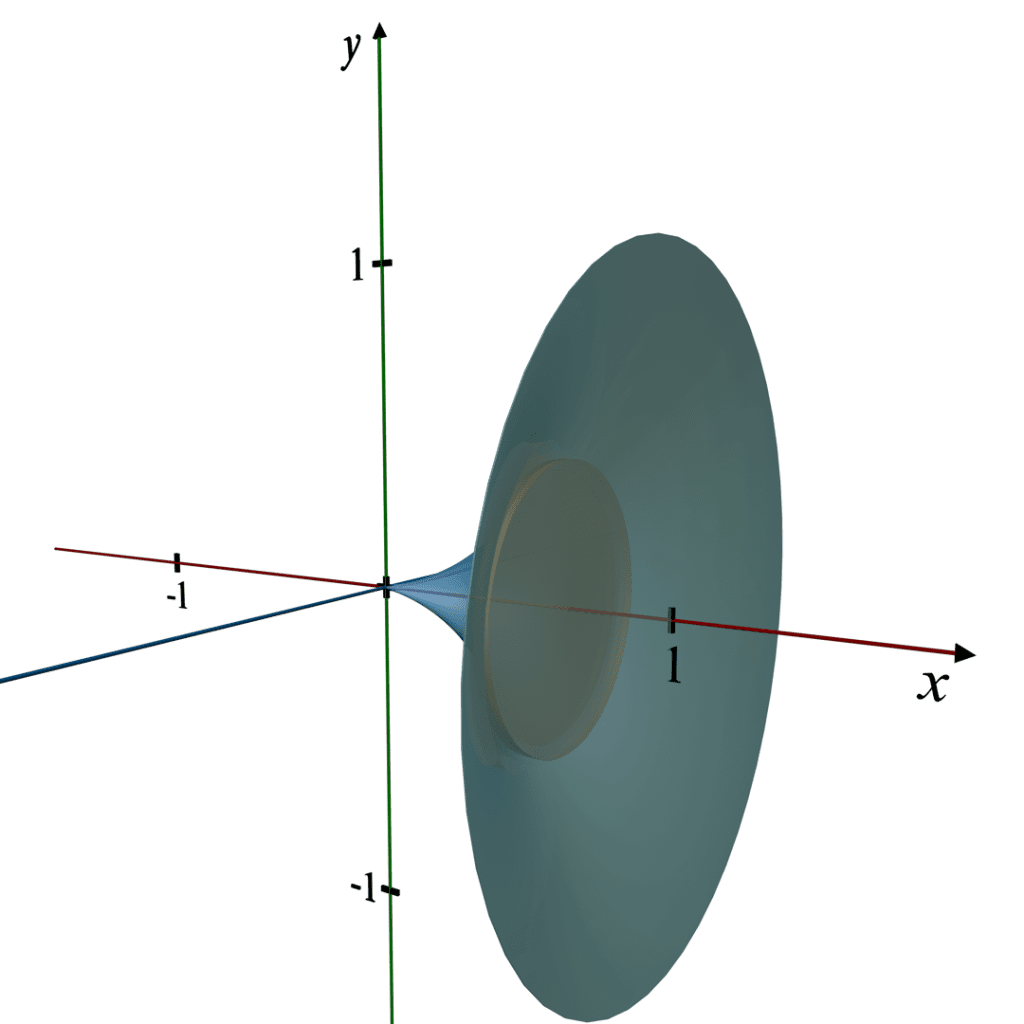
Visualizing the 3D Object:
Here is the 3D illustration of the solid formed by revolving the region bounded by
y = x2, the x - axis, and the line x = 1 about the x - axis.
This visualization shows a paraboloid, highlighting its shape and the curve that generates the solid.
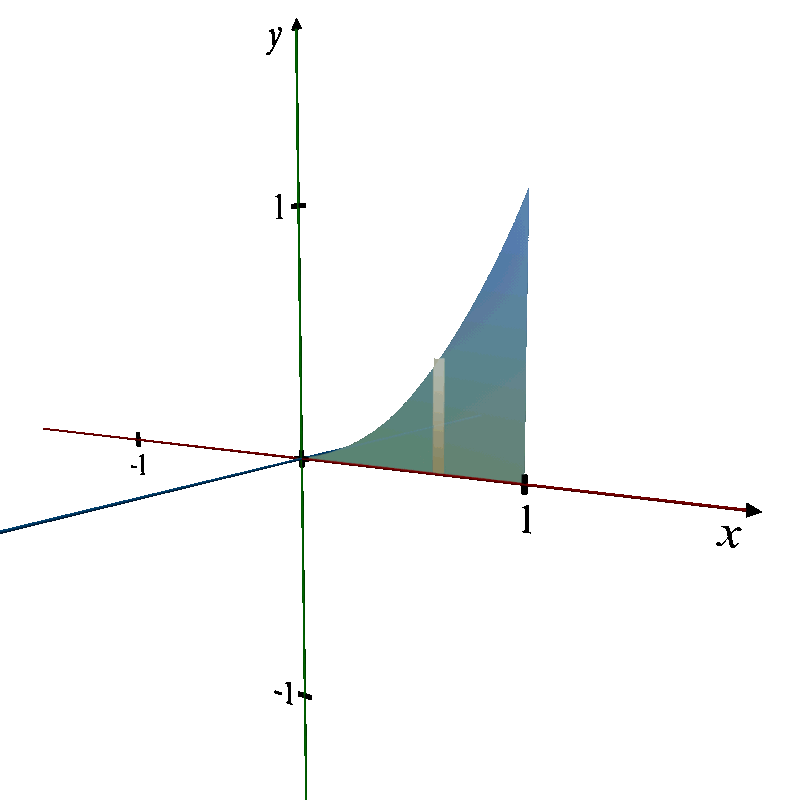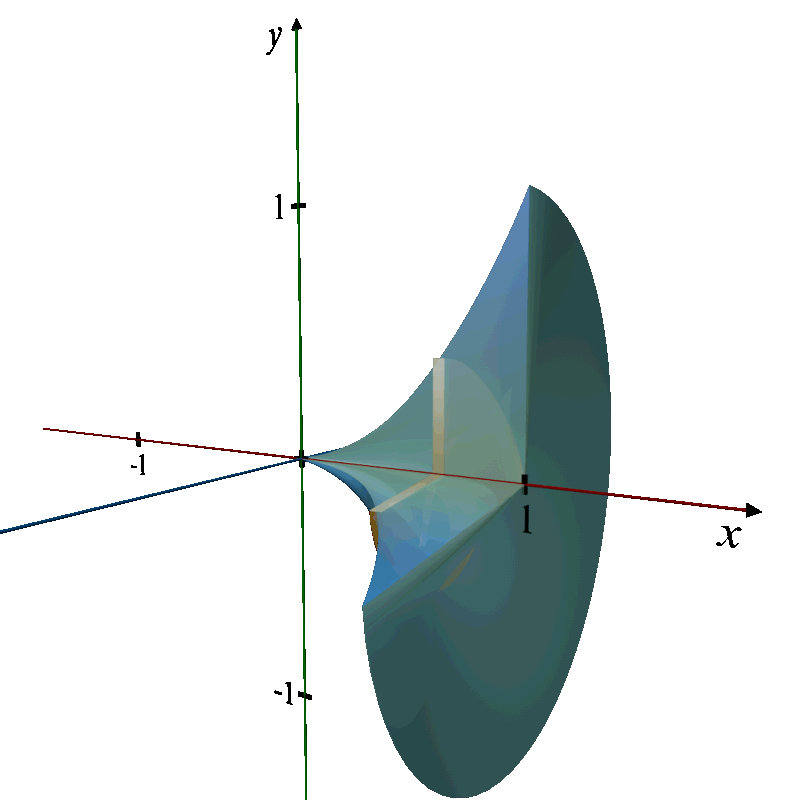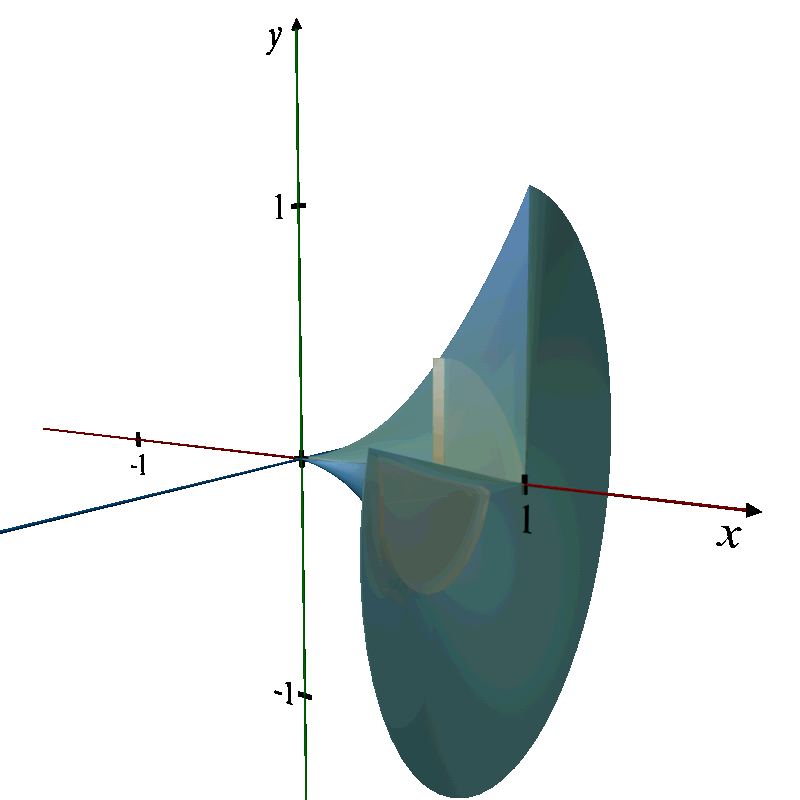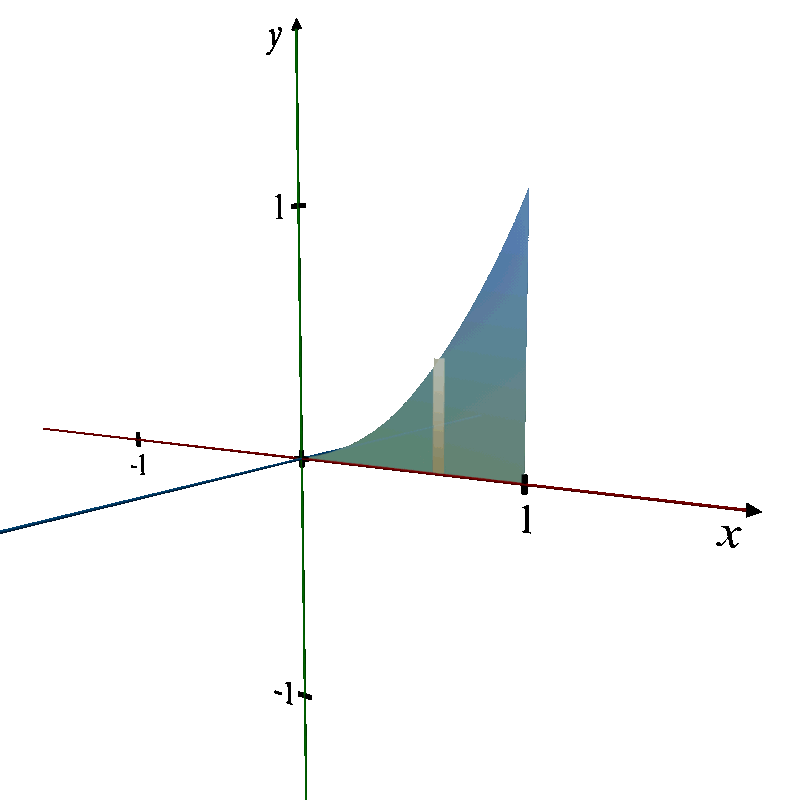
Q. 3. Find the volume of the solid formed by revolving the region bounded by the graph of the equation , the x - axis, covering the domain from x = 1 to x = 4, about the x - axis.
Recall that the volume of a solid formed when a curve is revolved about the x-axis is given by
Taking the constant (π) outside of the integral, we get:
Here, f(x) is the given function, which is y = x2. And since we are finding the volume of the solid formed when this curve is revolved about the x - axis from x = 1 to x = 4, the integral becomes:
This becomes:
Integrating, we get:
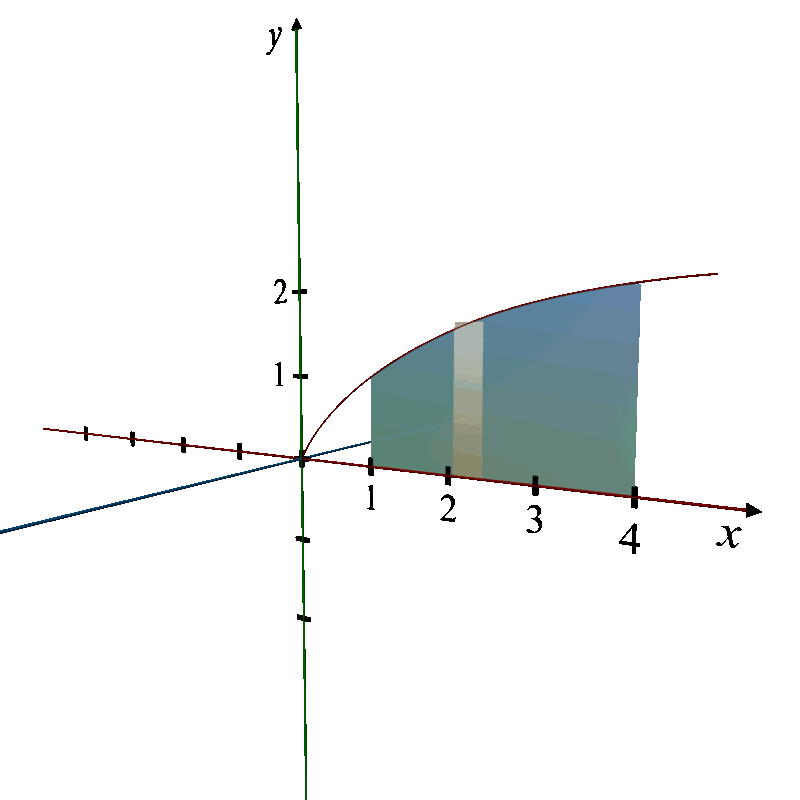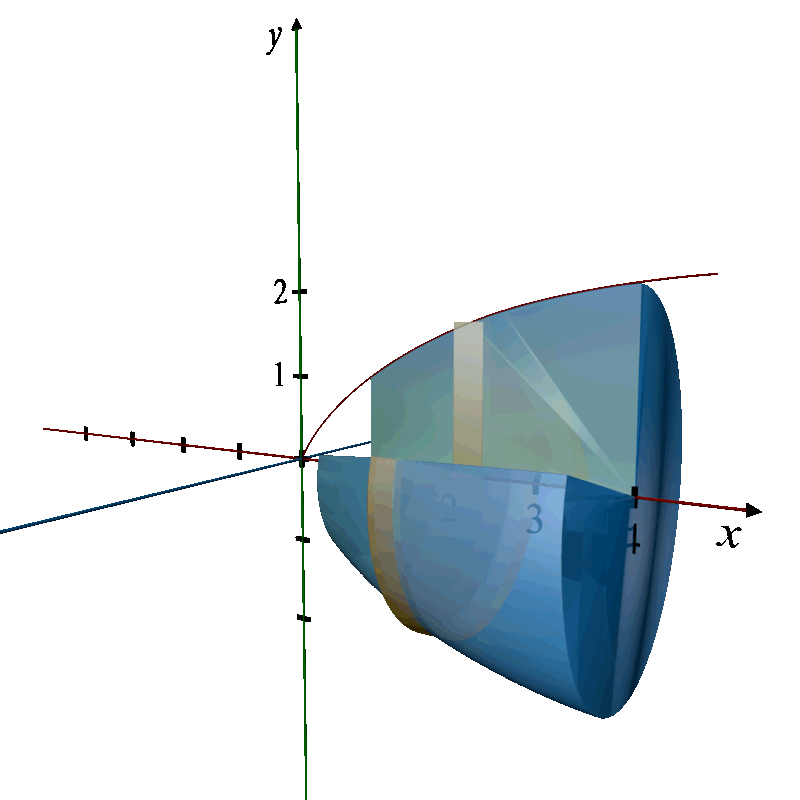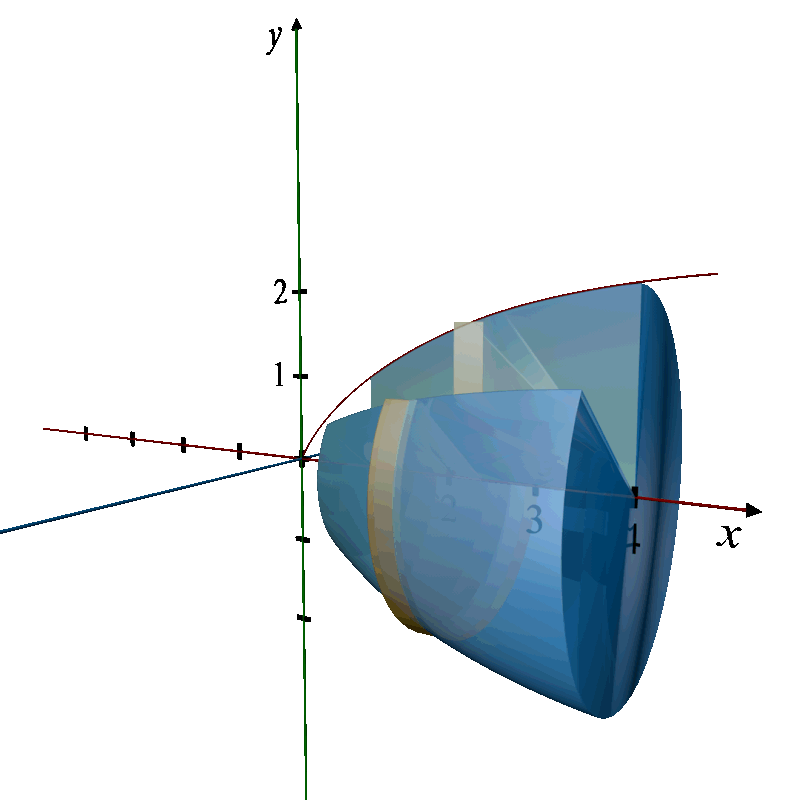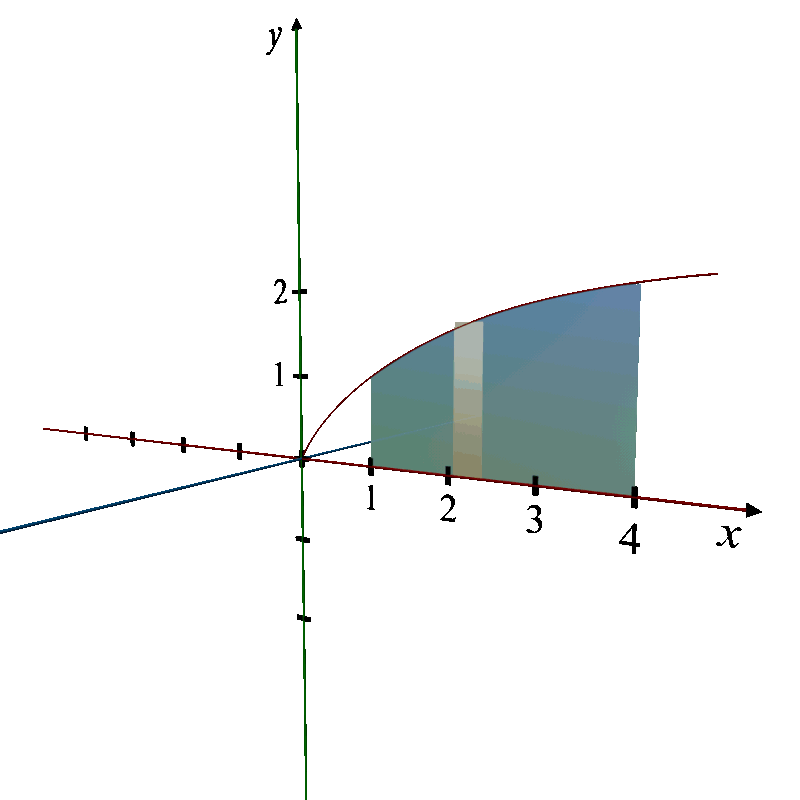
Shape Description
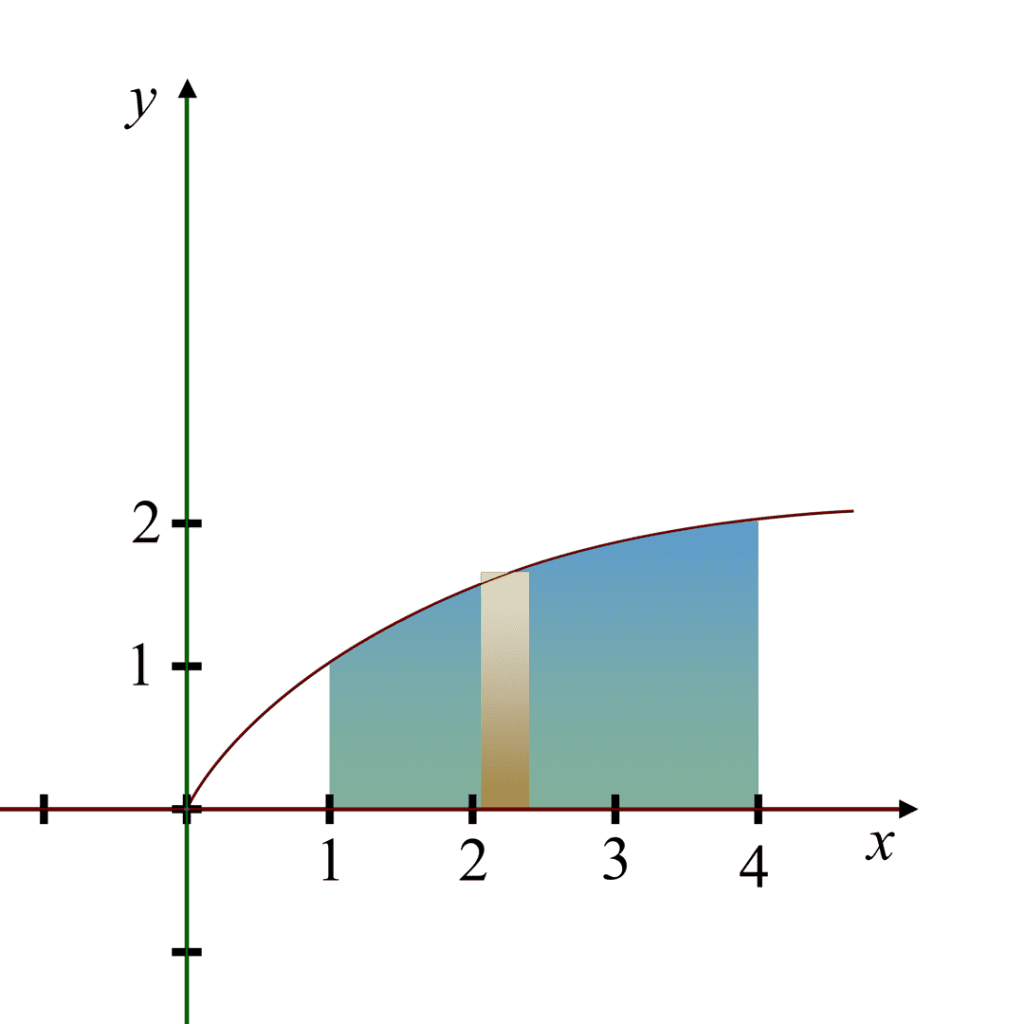
Region: The region is bounded by the curve
, the x-axis, and the vertical lines x = 1 and x = 4.
Revolution: When this region is revolved around the x-axis, it forms a 3D solid.
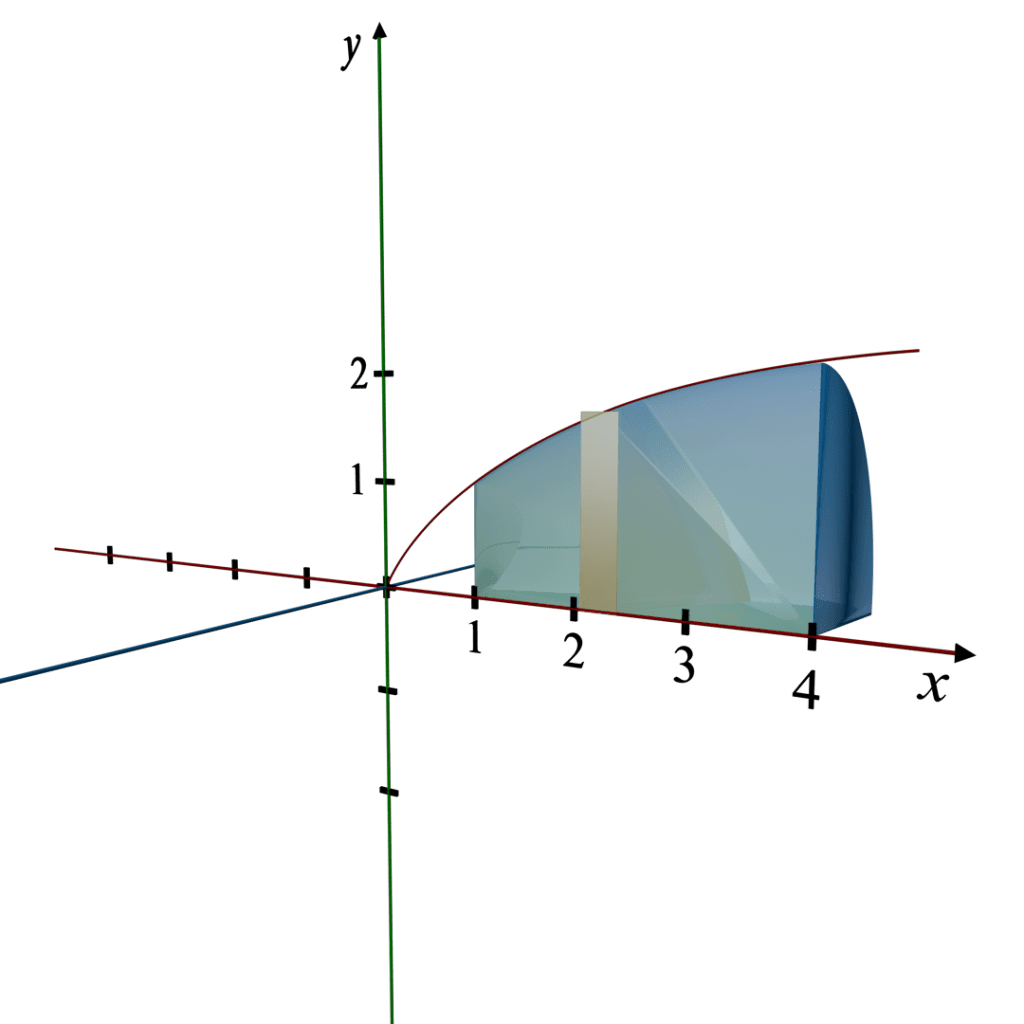
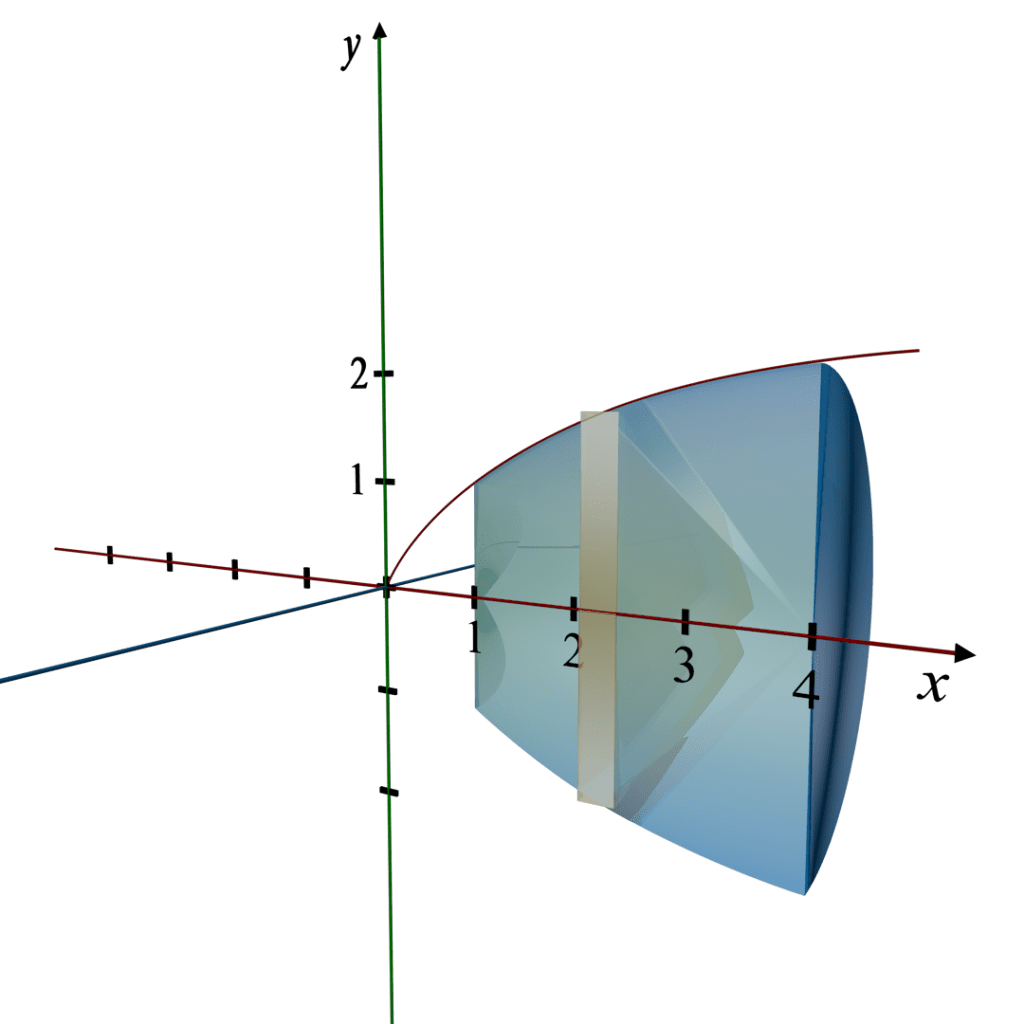
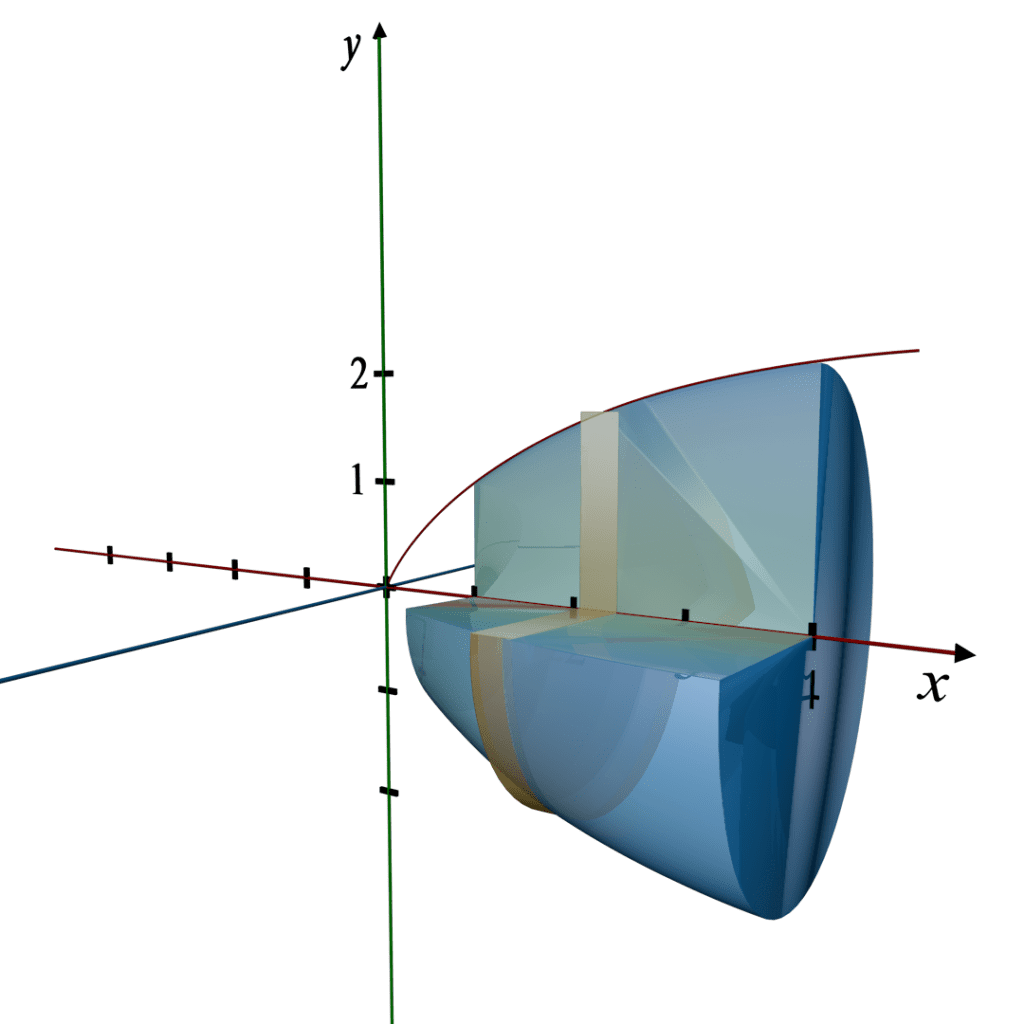
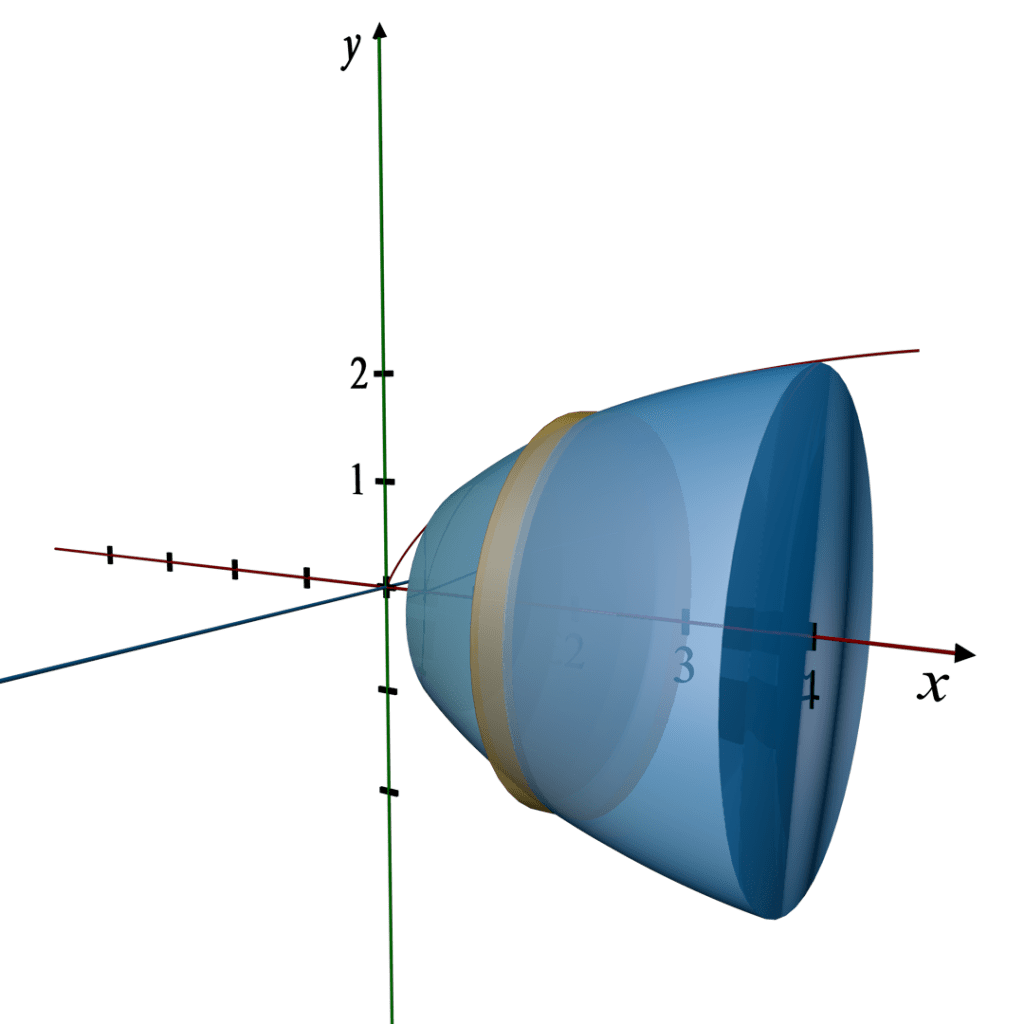
3D Revolution Description:
Solid of Revolution: The solid formed is a 3D shape known as a truncated cone, but with a curved rather than a straight side, narrowing as it extends from x = 4 back to x = 1.
Axis of Revolution: The x-axis.
Cross-section: Circular disks whose radii vary as the square root of x.
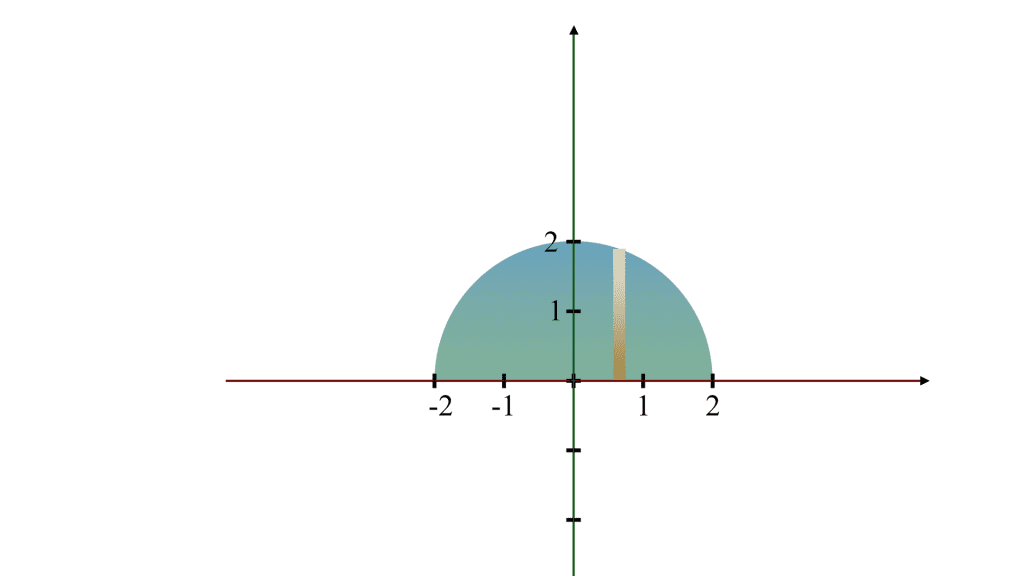
Q.4 Find the volume of the solid formed by revolving the region bounded by the graph of the equation , the x-axis, covering the domain from x = - 2 to x=2, about the x - axis.
Recall that the volume of a solid formed when a curve is revolved about the x-axis is given by.
Taking the constant (π) outside of the integral, we get:
Here, f(x) is the given function, which is y = x2. And since we are finding the volume of the solid formed when this curve is revolved about the x - axis from x = 1 to x = 4, the integral becomes:
This becomes:
Integrating, we get:
Shape Description:
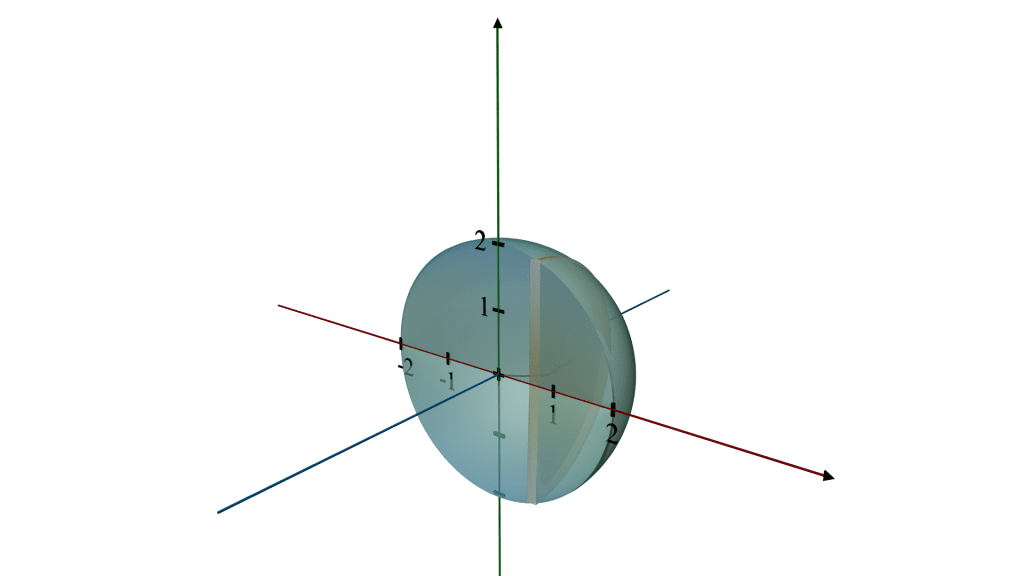
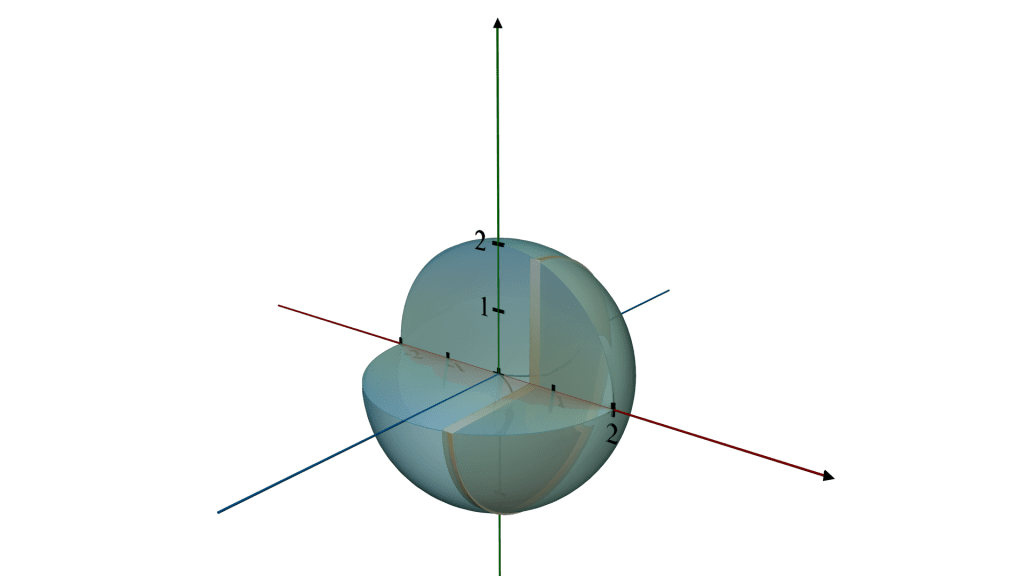
The original curve,
describes a semicircle with a radius of 2 centered at the origin, covering the domain from x = - 2 to x = 2 When this semicircle is revolved around the x - axis, it generates a complete sphere.
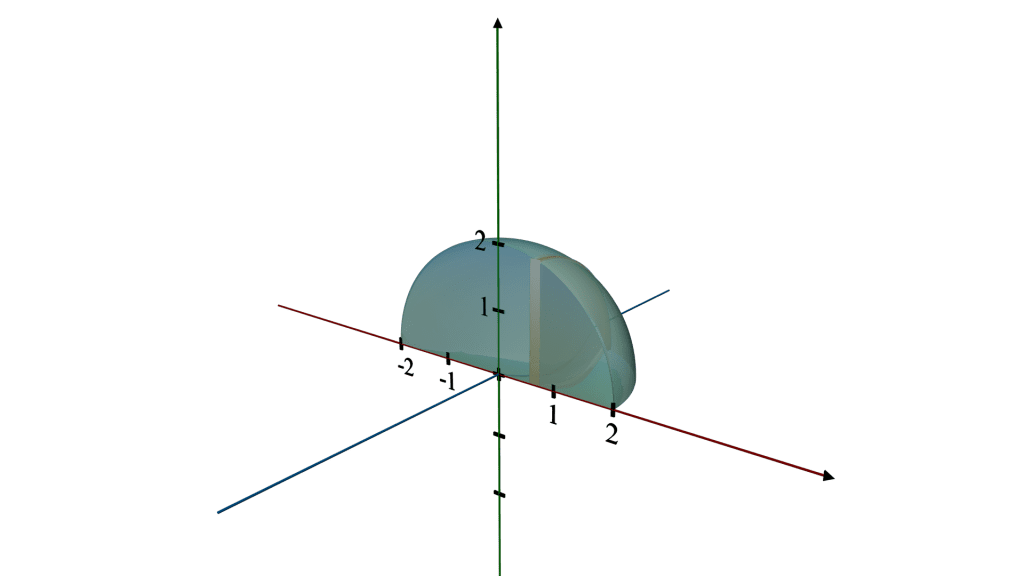

3D Revolution Description:
Imagine taking a half-circle cutout, and as you spin it around the x-axis (a line running horizontally through its center), the edges trace out the surface of a sphere.
Every point on the rim of the semicircle moves in a circular path around the x-axis, contributing to the spherical shape.
The result is a ball where every point on the surface is equidistant from the center, located at the origin (0,0).

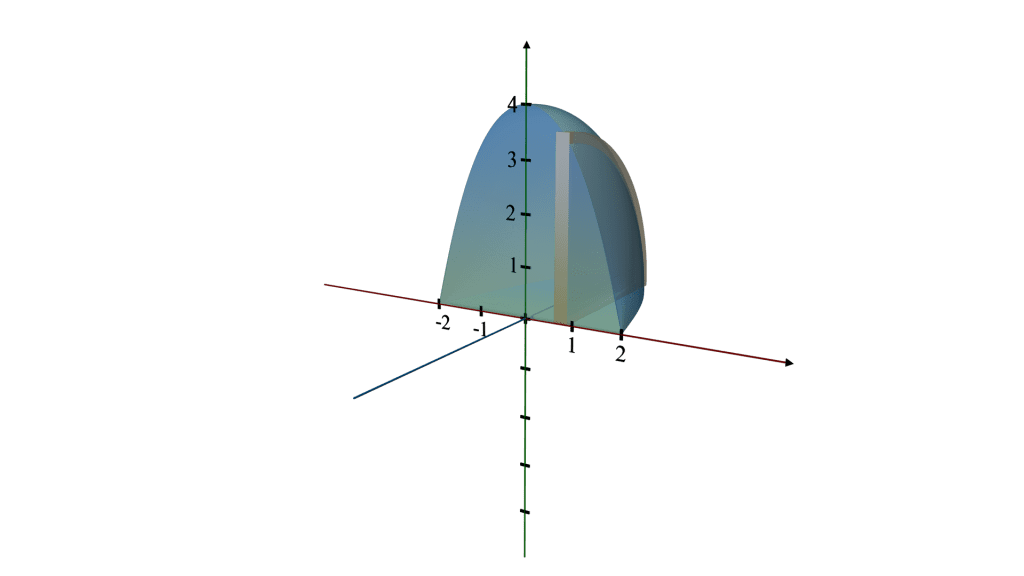
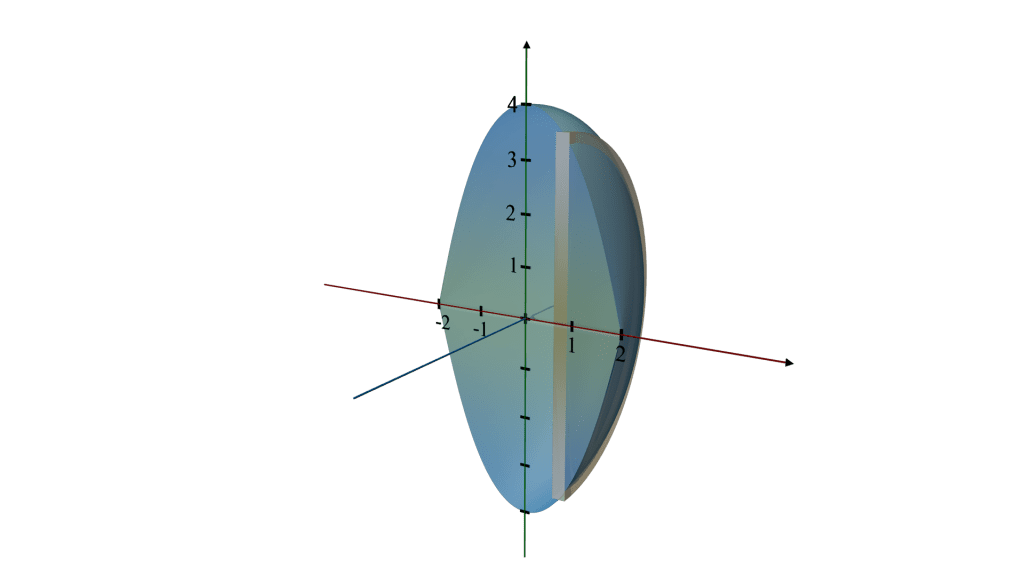
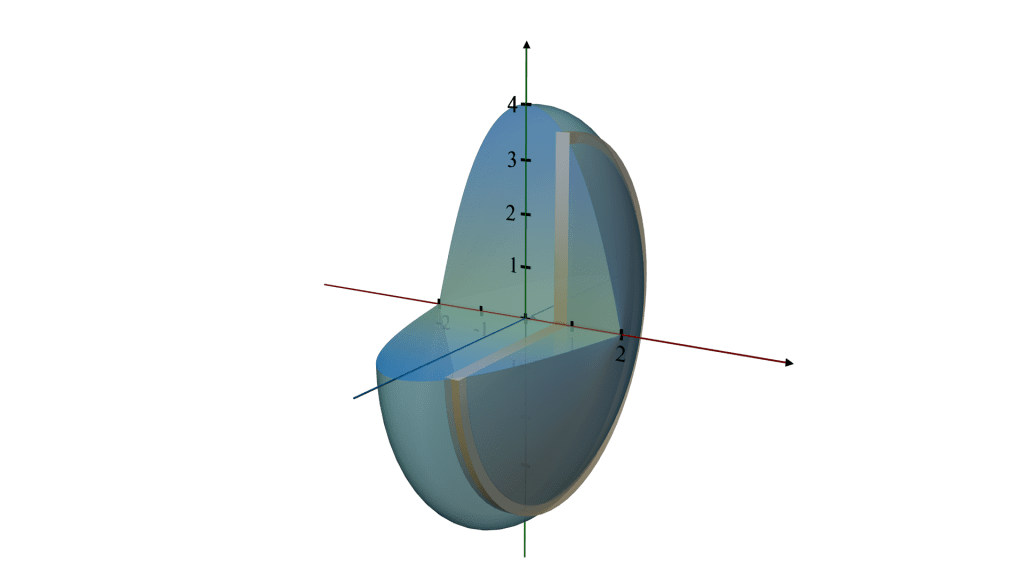
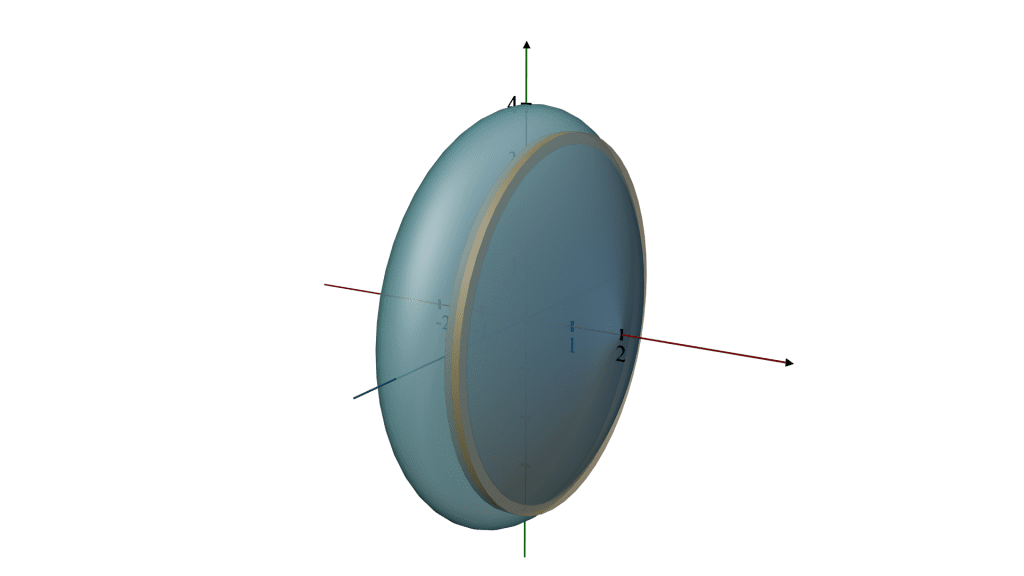
Q.5. Find the volume of the solid formed by revolving the region bounded by the graph of the equation y = 4 - x2 and the x - axis, about the x - axis.
Recall that the volume of a solid formed when a curve is revolved about the x-axis is given by
Taking the constant (π) outside of the integral, we get:
Here, f(x) is the given function, which is y = 4 - x2. And since we are finding the volume of the solid formed when this curve is revolved about the x - axis, we need to find the x - intercepts so we can find the boundaries which we will use to integrate our function.
The x - intercepts can be found by finding the zeros of the function. To find the zeros, we set the equation equal to zero, and solve for x.
Divide by -1 on both sides:
Square-root both sides:
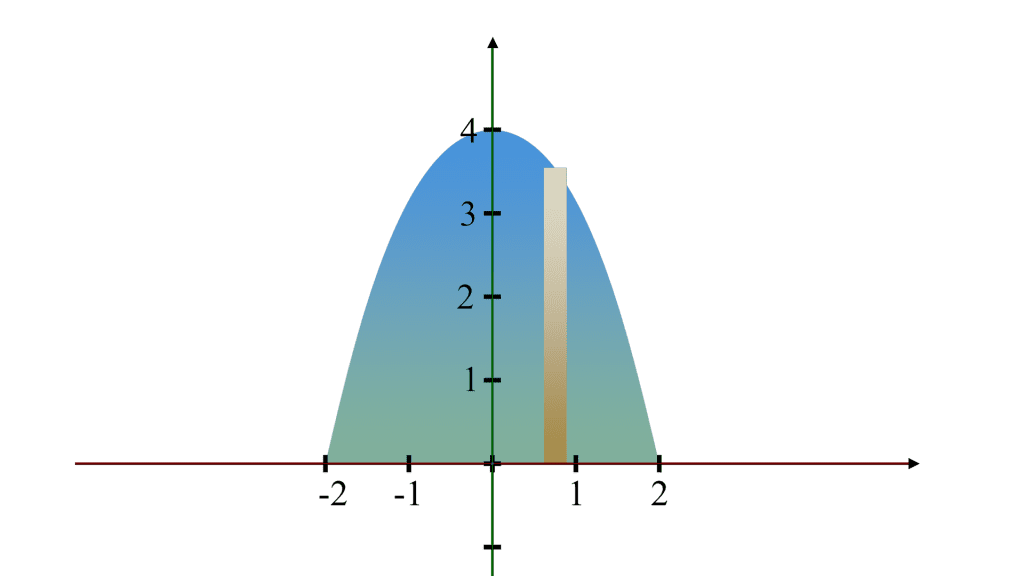
So the boundaries are a = - 2 and b = 2
Let’s now find the volume of the solid formed by integrating the function on this interval.
This becomes:
Expanding the binomials and simplifying, we end up with:
Integrating, we get:
The common denominator is 15, so this becomes:
Shape Description
:
Region: The region is bounded by the downward-facing parabola y = 4 - x2 and the x-axis. This parabola intersects the x-axis at points where y = 0, which are
x = - 2 and x = 2.