Optimize volume of cylinder while maintaining surface area Free (1)
In this project, we are going to take the measurements of an existing tuna can and find the existing volume. We will then be using algebra and calculus, as well as graphing, to find the new measurements of an optimized tuna can, one that will hold more product, but without changing the surface area of the can.
The idea is to maintain the surface area of the material being used so as to keep the cost of production unchanged, but allowing the manufacturer of the tuna to add more product within the can, if they wish to do so.
Tuna Can
Measurements taken
Height: 4.1 cm
Circumference: 27.2 cm
① Find the radius of the tuna can using the circumference
② Current Volume of the tuna can
③ Surface Area of the tuna Can
Left-Aligned MathML
math {
display: block;
margin-left: 0;
color: #0F9ED5; /* Setting the color as specified in mathcolor */
}
④ Use the surface area equation and rewrite it so we have h in terms of r.
Subtract 2πr2 on both sides
Divide both sides by 2πr to solve for h
⑤ Write the equation of the Volume of the tuna can in terms of r only, by substituting h with the expression obtained in step ④ above.
Rewriting the above equations in terms of x
⑥ Graph the volume equation on your GDC or desmos.com
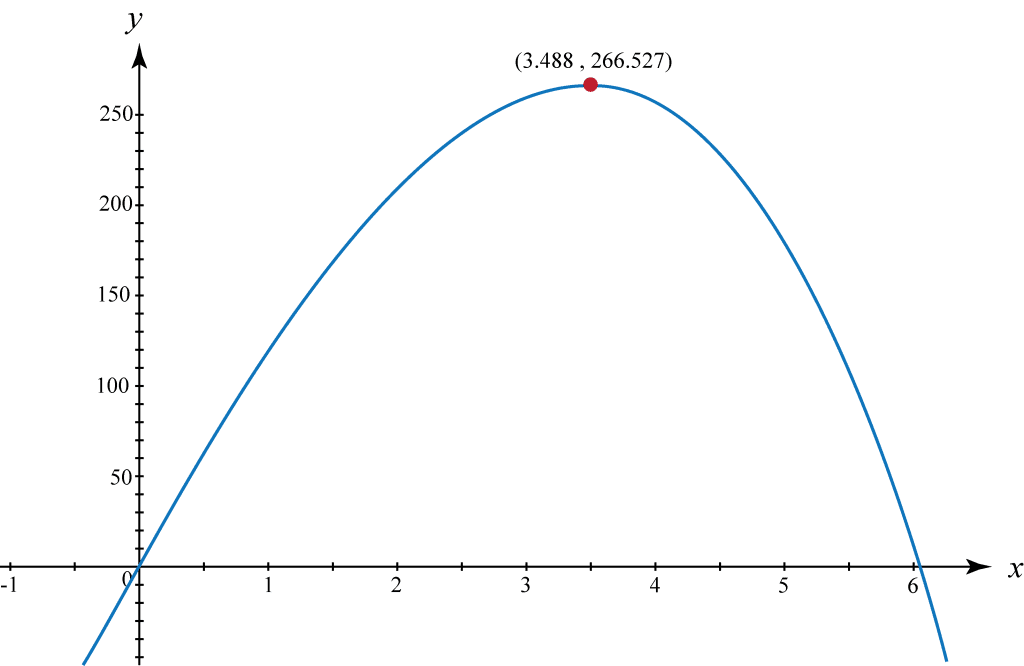
⑦ Finding the x-value (the radius) that maximizes the volume by taking the derivative of V(x), and setting V ' (x) = 0,
Setting V ' (x) = 0,
Divide both sides by - 3π
⑧ Substitute the value of x = 3.488 cm found in step ⑦ into the equation found in step ④ to find the height. This value is the radius, r, of the tuna can.
⑨ Substitute x = 3.488 cm found in step ⑦ into the volume equation to find the maximum volume.
⑩ We will now compare the volumes of the optimized tuna can with the original tuna can by dividing the existing volume with the existing volume and getting a percentage value.
The result above shows a 90.57% optimized tuna can. This means that the existing tuna can, with a volume equal to 90.57% of the optimized tuna can, can have its volume increased to hold more tuna whilst maintaining the same surface area, so as to not increase the cost of material used in the production of the tuna can.
The optimized tuna can will have
The following measurements:
Height: 6.975 cm
Radius: 3.488 cm
Applications of Optimizing the Volume of a Cylinder While Maintaining Surface Area
Optimizing the volume of a cylinder while maintaining its surface area has several practical applications across various fields. Here are some key examples:Optimize Volume Of Cylinder
1. Packaging and Manufacturing
Container Design: In the packaging industry, optimizing the volume of cylindrical containers (like cans and bottles) while maintaining a specific surface area helps minimize material usage and costs while maximizing storage capacity. This is crucial for both economic and environmental reasons.Optimize Volume Of Cylinder
Efficient Use of Materials: Manufacturers aim to design containers that use the least amount of material for a given volume, reducing waste and production costs. This is particularly important for products such as food, beverages, and pharmaceuticals.Optimize Volume Of Cylinder
2. Engineering
Storage Tanks: Engineers design storage tanks for liquids (such as water, oil, and chemicals) with optimal volume while maintaining a fixed surface area to ensure structural integrity and cost efficiency. This is vital in industries such as oil and gas, water treatment, and chemical processing.Optimize Volume Of Cylinder
Heat Exchangers: In thermal engineering, the optimization of cylindrical components in heat exchangers can improve efficiency. Maintaining a fixed surface area while optimizing volume can lead to better thermal performance and reduced material costs.Optimize Volume Of Cylinder
3. Environmental Science
- Waste Management: Optimizing the volume of cylindrical waste containers (like bins and tanks) while maintaining a specific surface area can help in designing more efficient waste storage solutions. This is essential for waste management and recycling programs.Optimize Volume Of Cylinder
4. Food and Beverage Industry
Maximizing Product Storage: Beverage companies often optimize the volume of cylindrical containers (like soda cans) to maximize the amount of product they can store and transport while maintaining a fixed surface area to keep production costs low and ensure stackability.Optimize Volume Of Cylinder
Efficient Transportation: Optimized container designs lead to more efficient use of space during transportation, reducing the number of trips needed and, consequently, the carbon footprint.Optimize Volume Of Cylinder
5. Pharmaceuticals
- Pill Bottles and Vials: Pharmaceutical companies optimize the volume of cylindrical pill bottles and vials to ensure they contain the maximum number of pills or the maximum volume of liquid medicine while using minimal material. This ensures cost-effective production and ease of handling.Optimize Volume Of Cylinder
Graphs of Inverse Trigonometry Functions
AREAS btw CURVES and VOLUMES of REVOLUTIONS
Word to JPEG – Convert Word files to JPEG Images Online
WebP to JPEG – Convert WebP to JPEG
HEIC to JPG – Convert HEIC Images to JPEG Format