Measure of an exterior angle of a Regular Polygon
What is a regular polygon? A polygon is an enclosed shape, with straight edges that has three sides or more. Some examples of polygons are triangles, quadrilaterals, pentagons, hexagons, octagons, and so on….

In a polygon, the measures of the sides don’t necessarily have to be equal.
A regular polygon, on the other hand, is one in which all the sides have the same length.
An equilateral triangle is an example of a regular polygon, since all the sides are equal, and all the interior angles are equal as well.
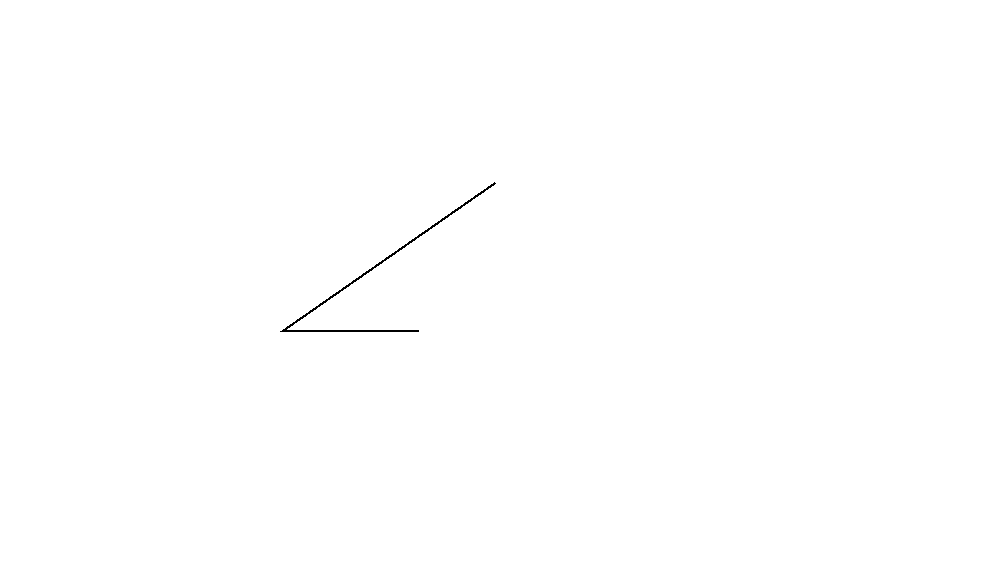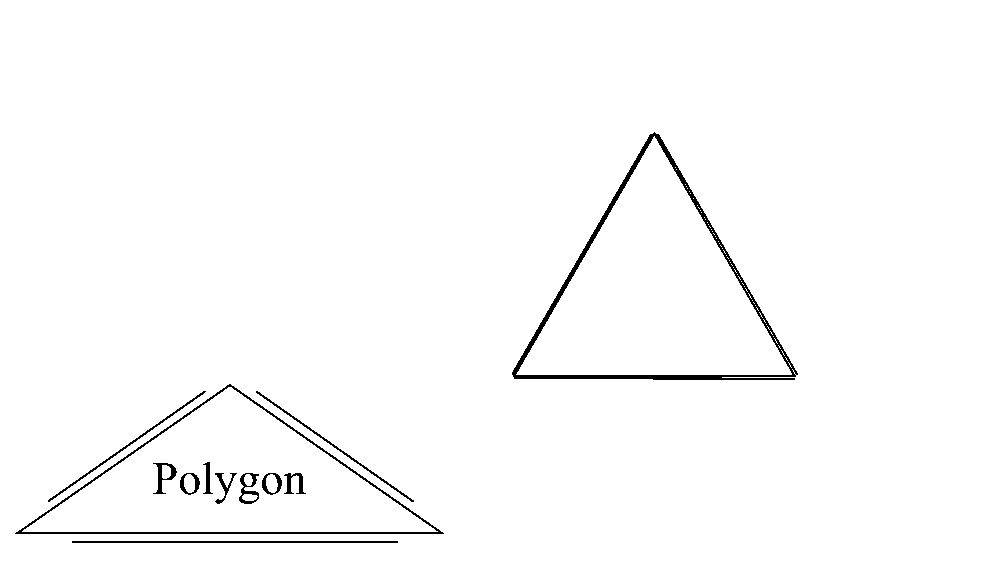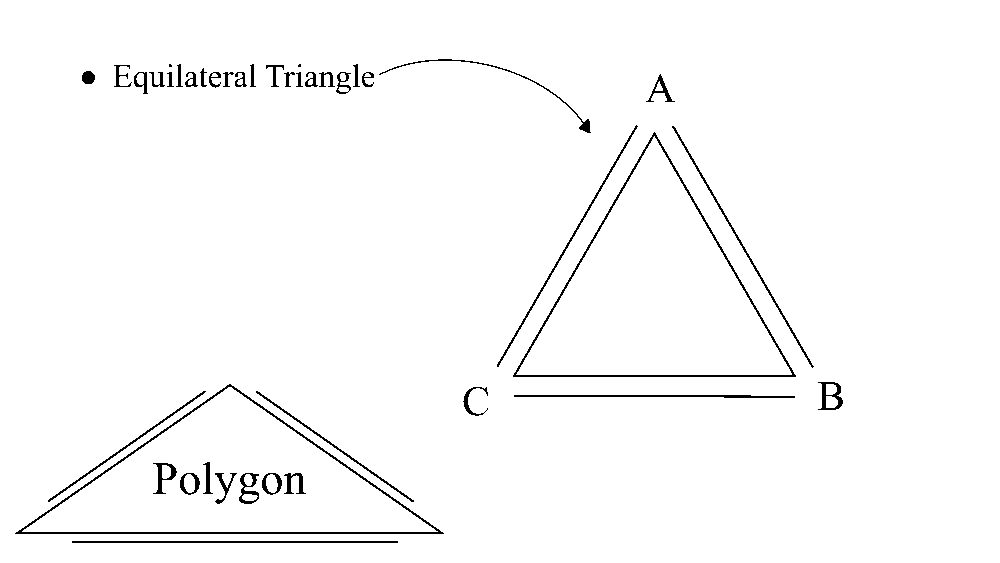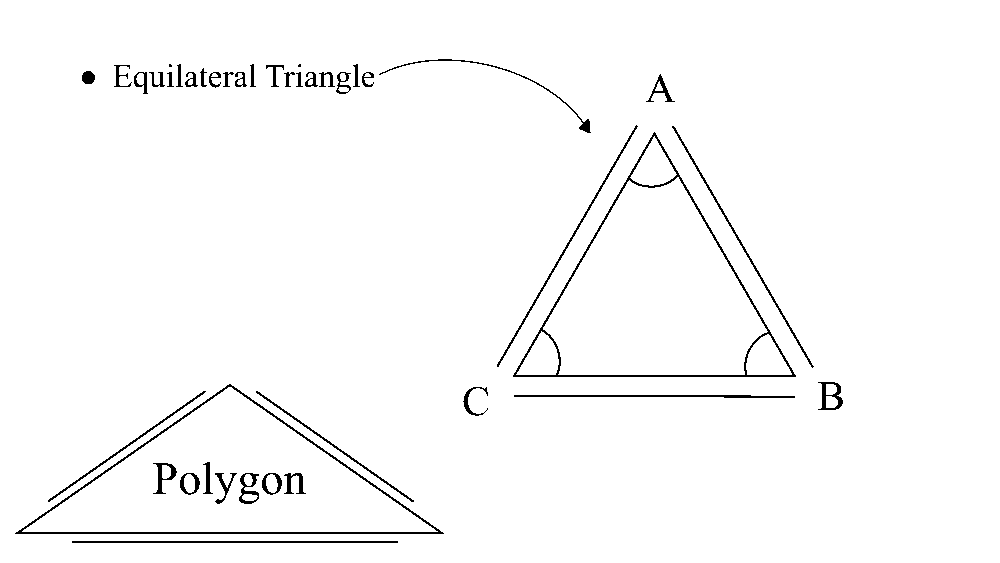
A square is an example of a quadrilateral that is a regular polygon. All the sides are equal and each interior angle is equal to 90 degrees.

All regular polygons have side lengths that are equal and interior angles that are equal to each other, but the exterior angles also happen to be the same.

Take a look at the equilateral triangle below. An equilateral triangle has three congruent sides, which means all three sides have the same length. What is also equal, is the measure of each angle. So we say the triangle is also equiangular.
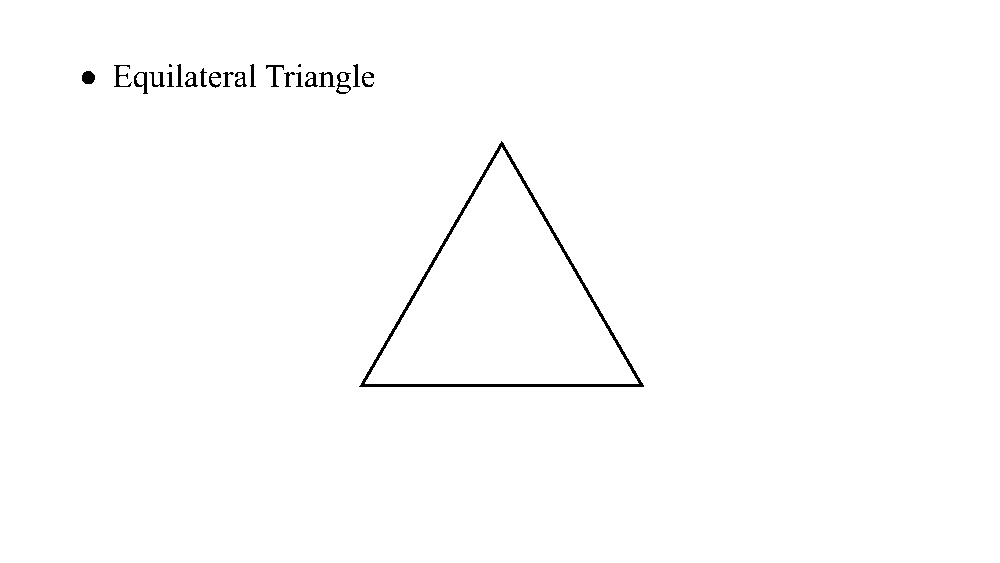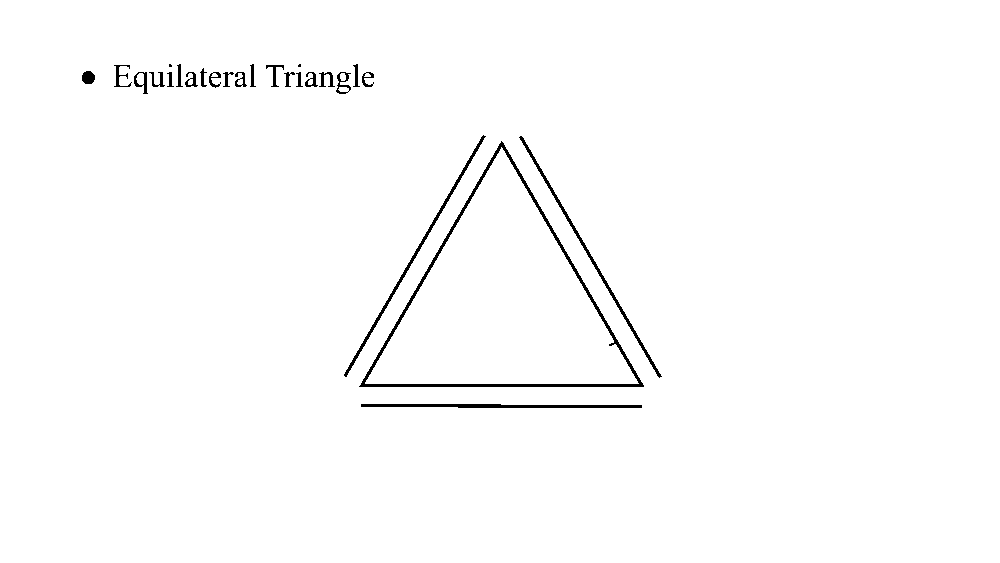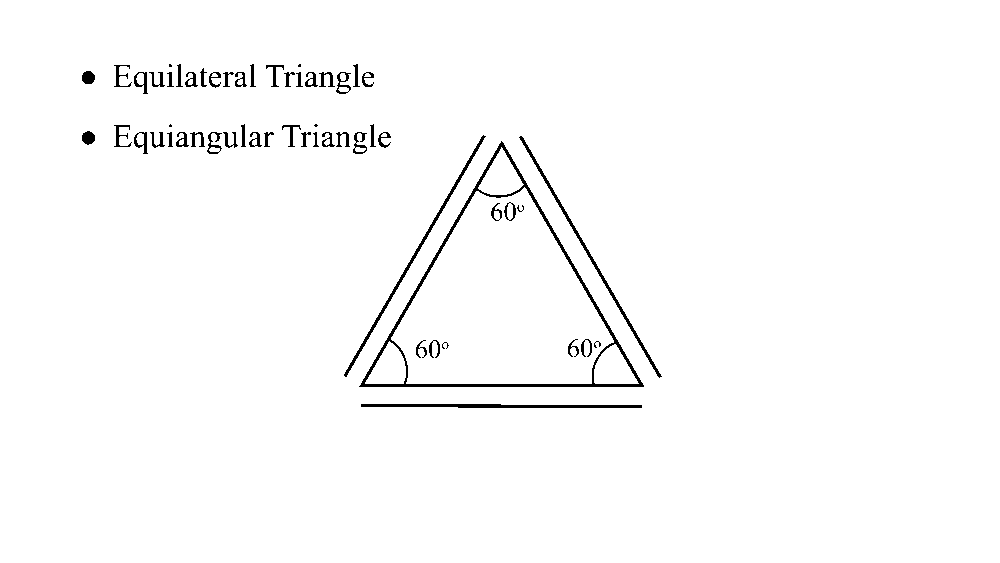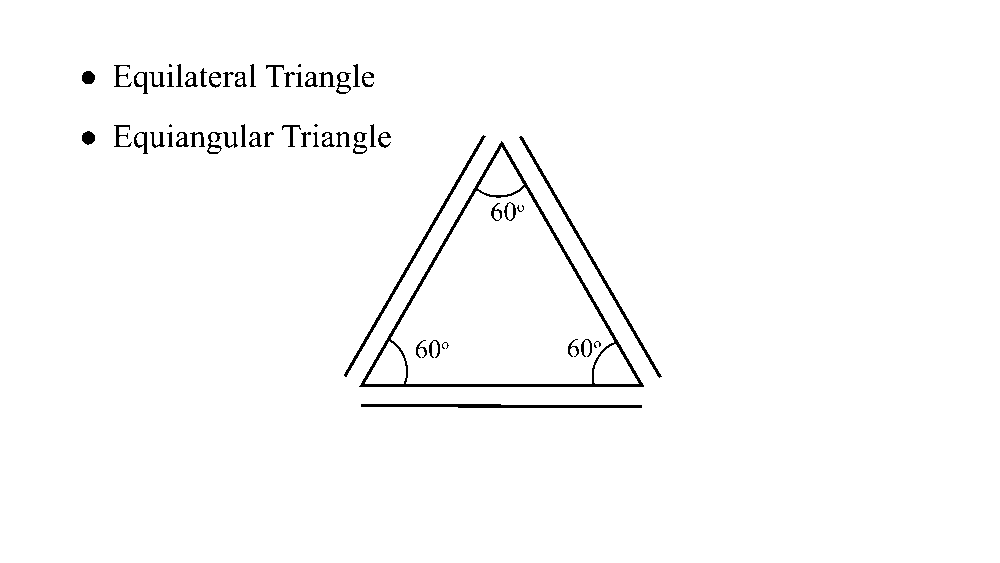
Now, we know that the sum of all angles in a triangle is 180°. In an equilateral triangle, each angle is then equal to 180° divided by 3, which is 60°.
Each exterior angle, which is supplementary to the interior angle, is then equal to 180° minus 60°, which is equal to 120°.
We can find the measure of any exterior angle by first finding the measure of each interior angle and then subtracting it from a hundred and eighty.
The equation that is used in mathematics to find the sum of the interior angles of a polygon is
(n-2)×180°, Where n is the number of sides.
Geometry Table with Fractions
body {
font-family: Arial, sans-serif; /* Ensures a clean, readable font */
margin: 20px; /* Provides some spacing around the table */
}
table {
width: 100%; /* Makes the table stretch to fill the container */
border-collapse: collapse; /* Eliminates the gap between borders */
table-layout: fixed; /* Helps keep columns evenly spaced */
}
th, td {
border: 1px solid black; /* Adds a black border around each cell */
padding: 10px; /* Adds space inside each cell */
text-align: center; /* Centers the text horizontally in cells */
}
th {
background-color: #e0e0e0; /* A light grey background for header cells */
}




In each shape, the exterior angle is equal to 180° minus the interior angle.
So in a regular triangle, the exterior angle is 180° - 60°, which equals to 120°.
In a square, the measure of each exterior angle is 180° - 90°, which equals to 90°.
In a pentagon, the measure of each exterior angle is 180° - 108°, which equals to 72°.
Similarly, for a hexagon, the measure of each exterior angle is 180° - 120°, which equals to 60° degrees.
Geometry Table with Fractions
body {
font-family: Arial, sans-serif; /* Ensures a clean, readable font */
margin: 20px; /* Provides some spacing around the table */
}
table {
width: 100%; /* Makes the table stretch to fill the container */
border-collapse: collapse; /* Eliminates the gap between borders */
table-layout: fixed; /* Helps keep columns evenly spaced */
}
th, td {
border: 1px solid black; /* Adds a black border around each cell */
padding: 10px; /* Adds space inside each cell */
text-align: center; /* Centers the text horizontally in cells */
}
th {
background-color: #e0e0e0; /* A light grey background for header cells */
}
But is there a way to calculate the measure of each exterior angle without finding the interior angles first?
And the answer is yes. Let’s take a look at some regular polygons below.
Let’s start with a regular triangle. Let’s take a look at all the exterior angles. Each of them is 120°.
If we shrink the shape down to a dot, look at what happens to the exterior angles. Al three form a full circle. Which means the angles add up to 360°
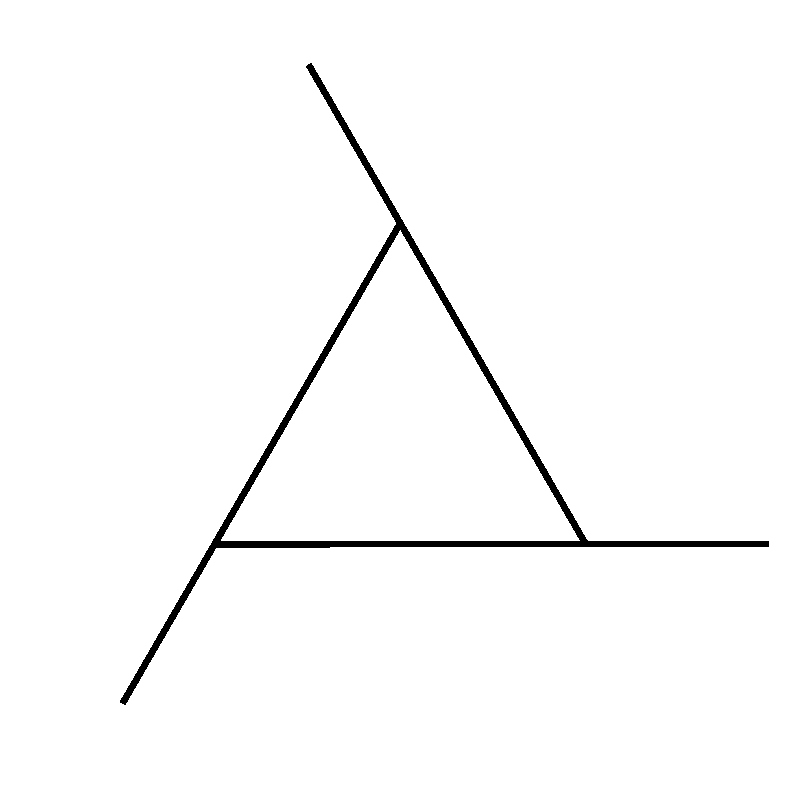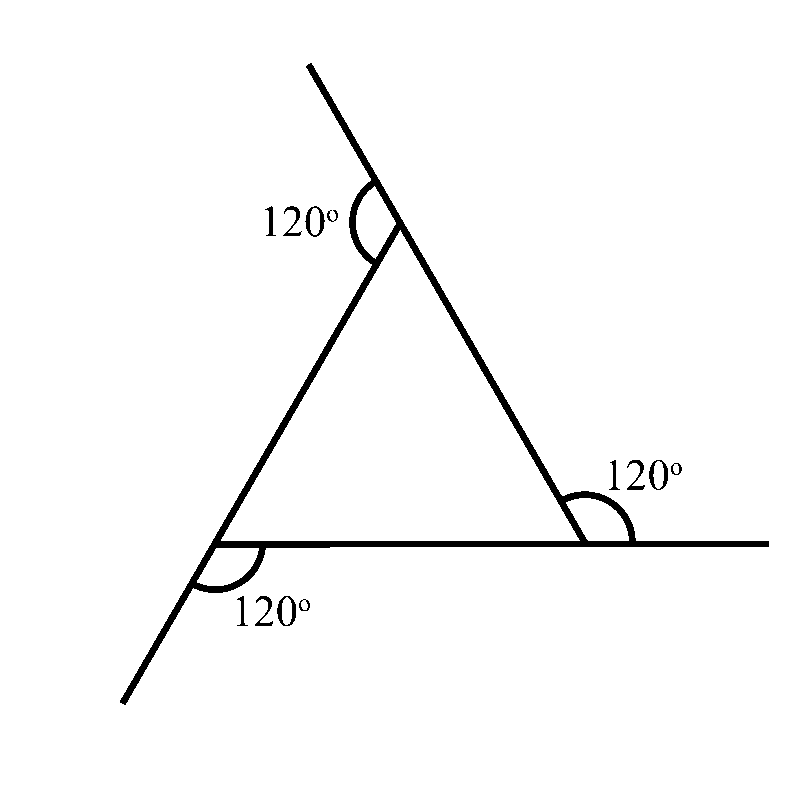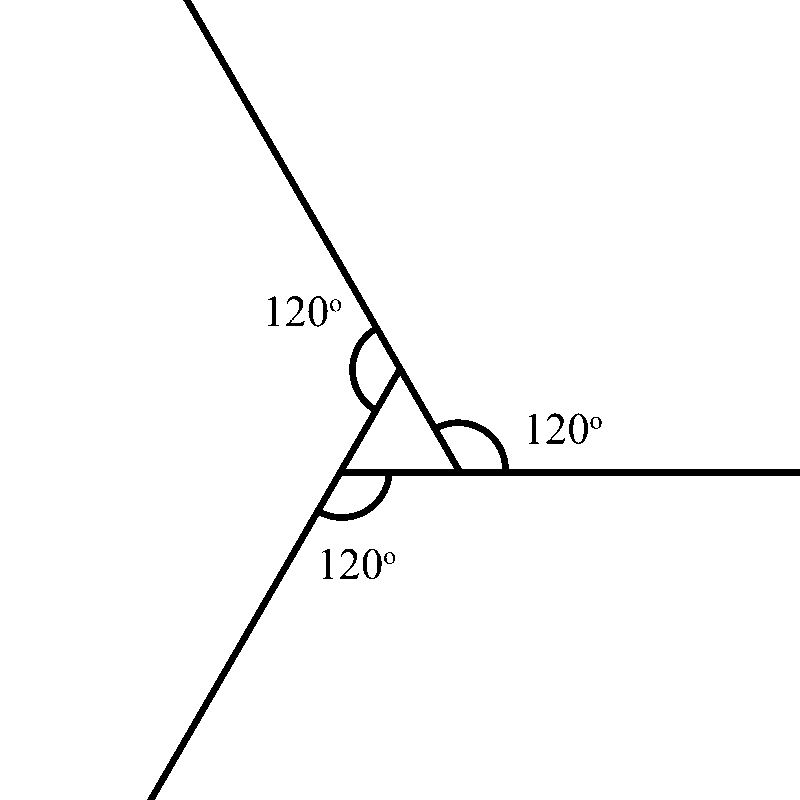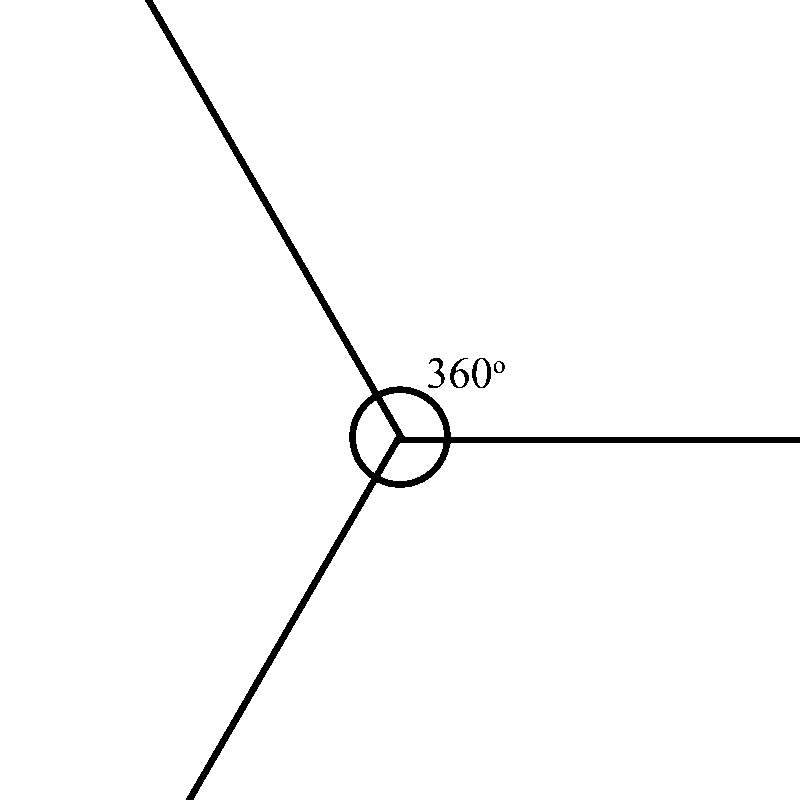
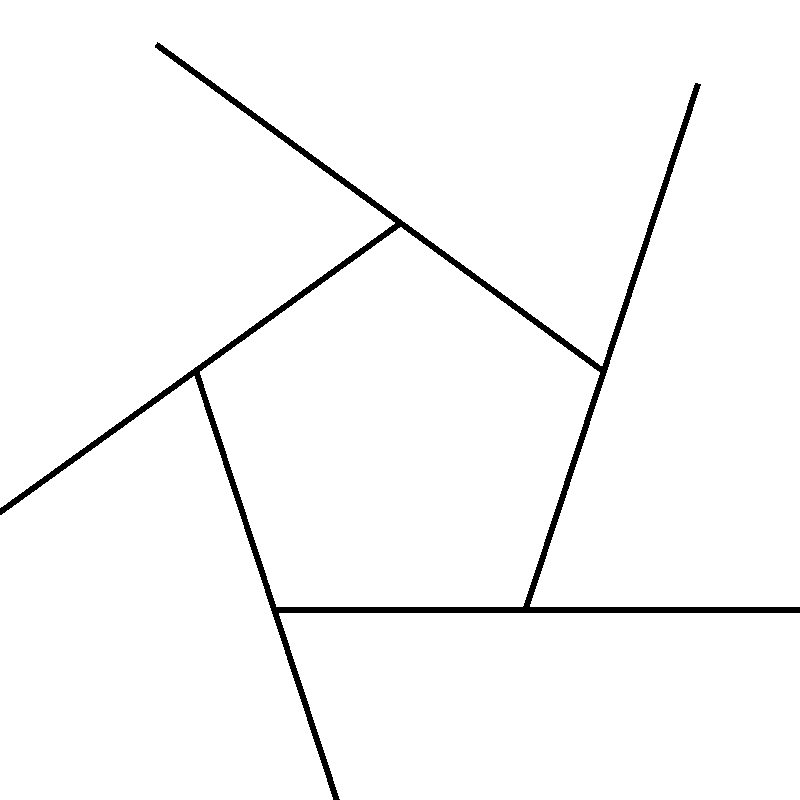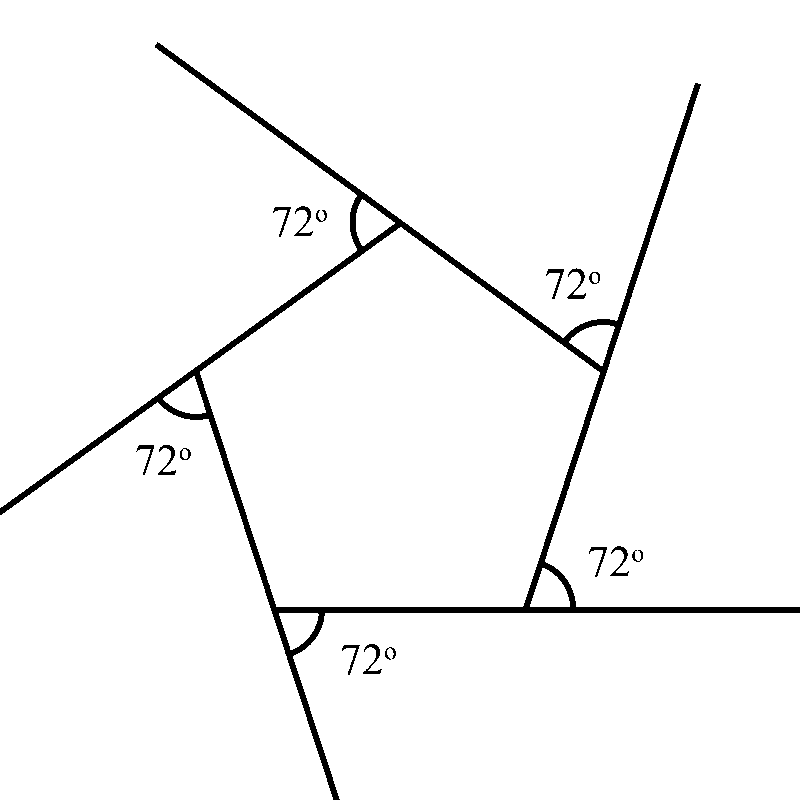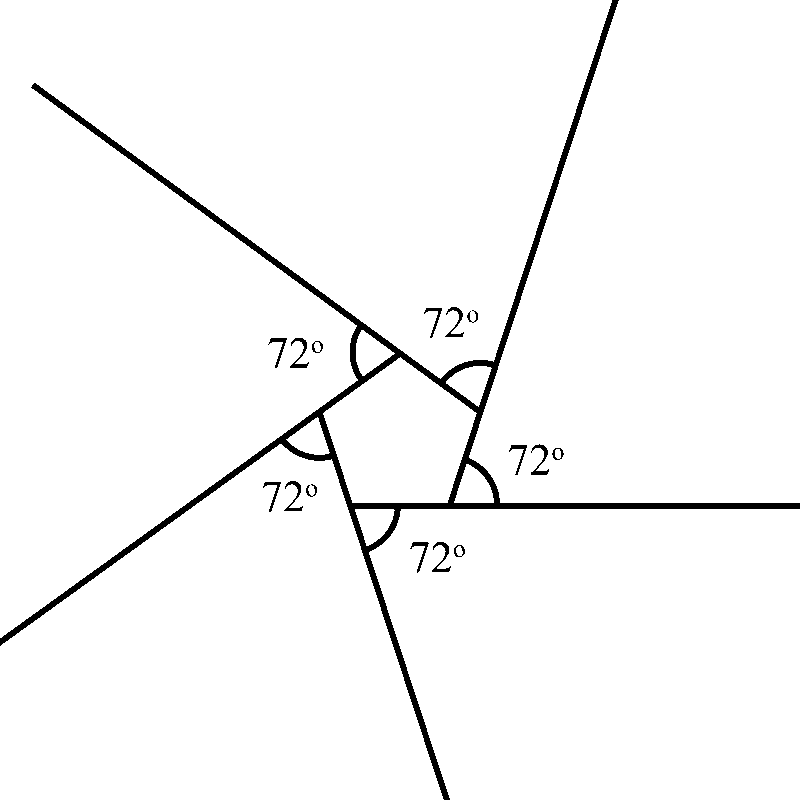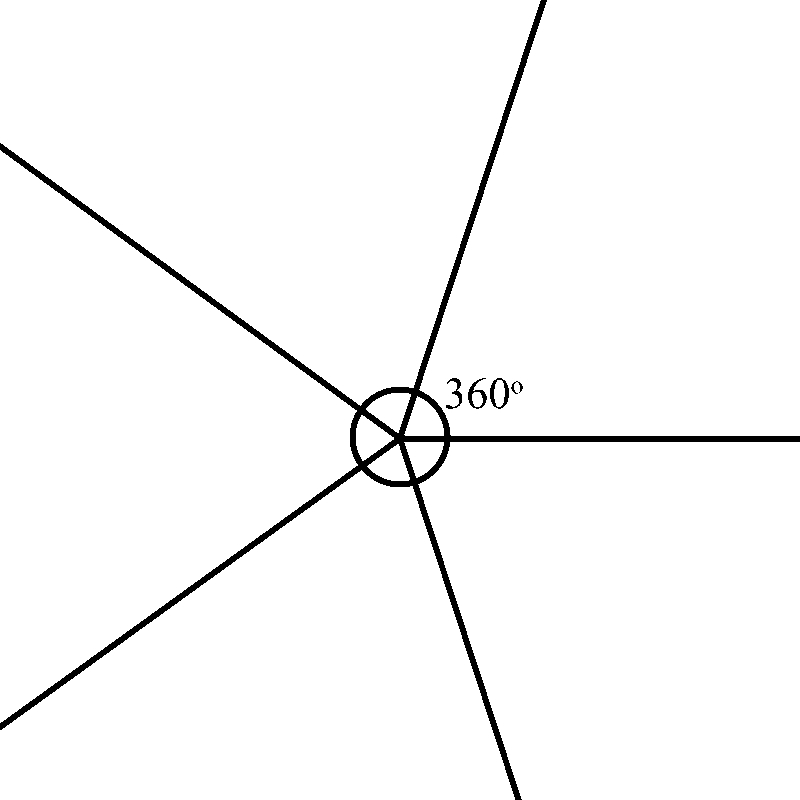
Taking a pentagon, there are five exterior angles, each one measuring 72°.
Shrinking this shape down to a dot, all five angles form a full circle, once again.
This means that the angles add up to 360°
Let’s look at a hexagon below.
A hexagon is a six-sided polygon. In a regular hexagon, there are 6 exterior angles, each one measuring 60°.
Once again, we shrink this shape down to a dot, and, as we expected, the angles form a circle, since all six angles add up to 360°
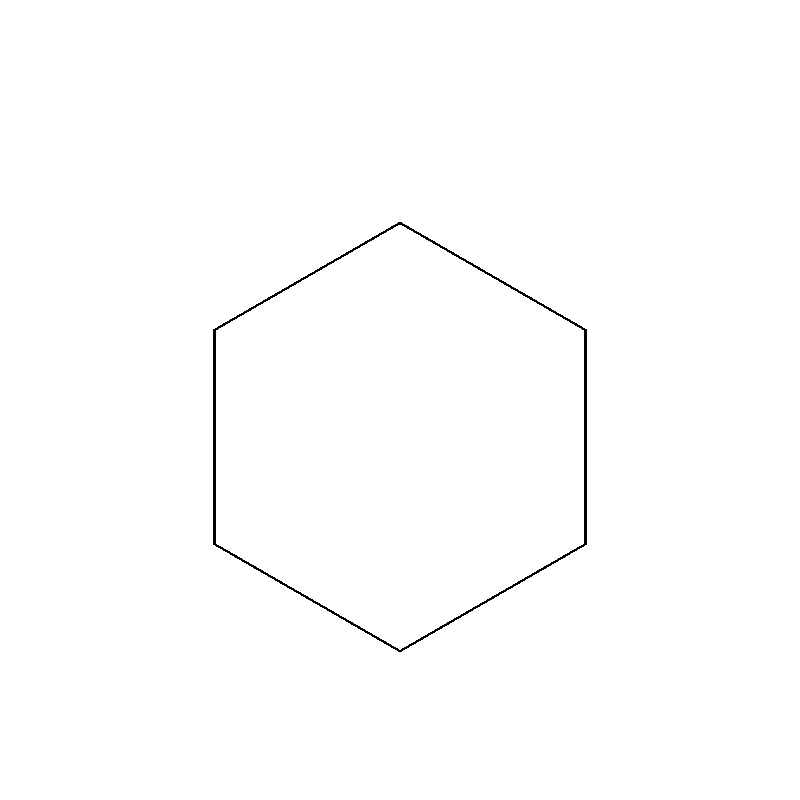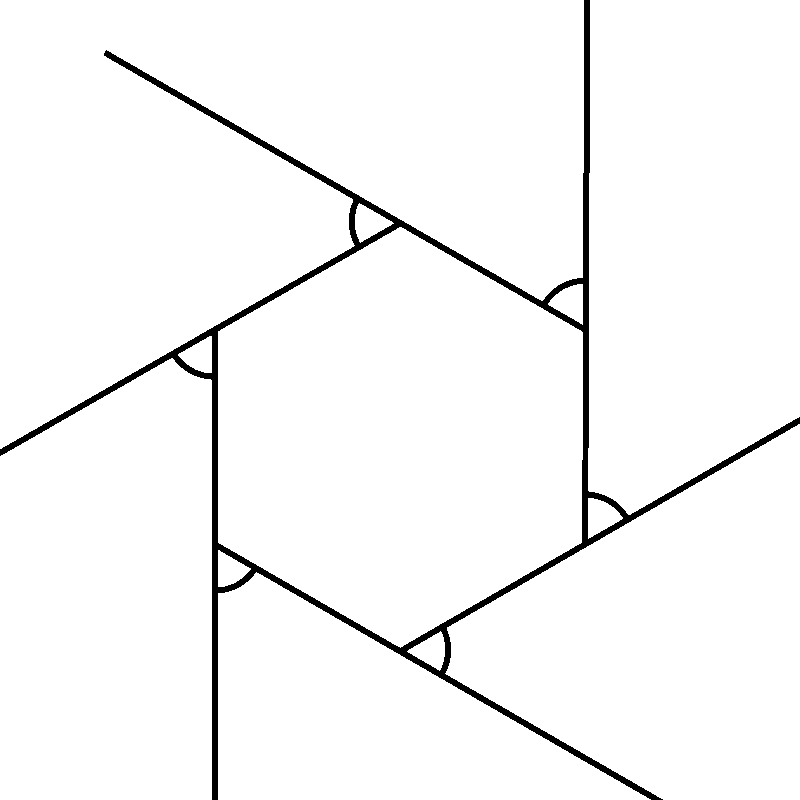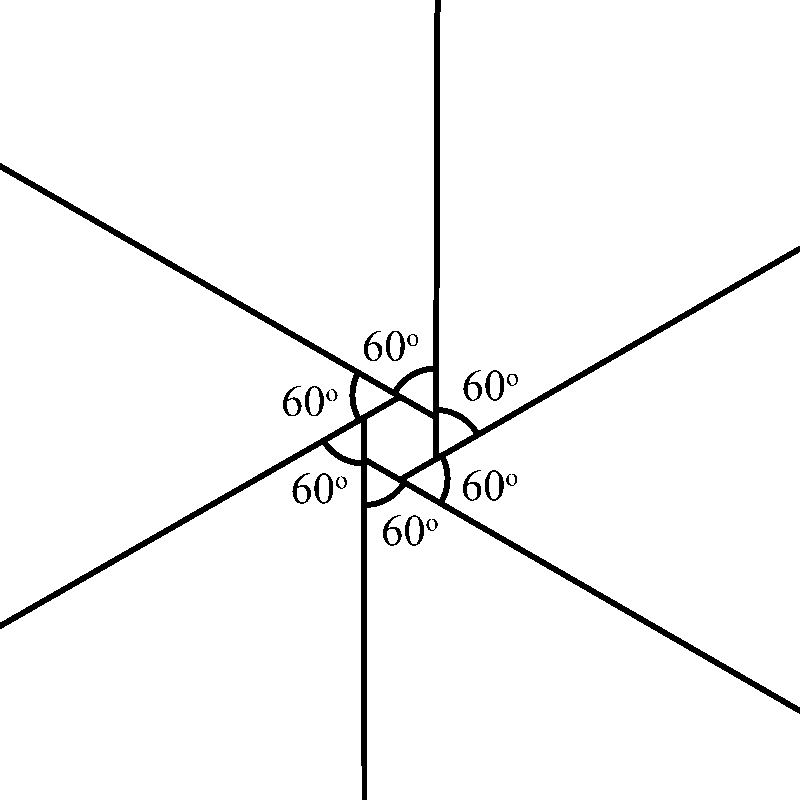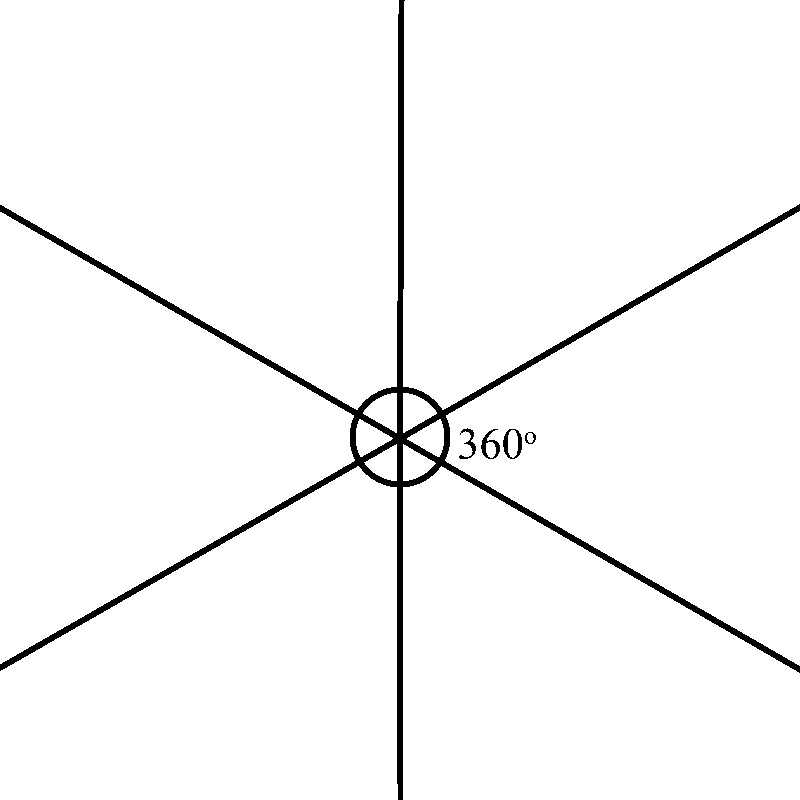
With this knowledge, we can now figure out the measure of an exterior angle of any regular polygon by simply dividing 360 by the number of sides.
For example, a heptagon below, a 7-sided shape, will have an exterior angle measuring

A regular octagon below, an eight-sided shape, will have an exterior angle measuring
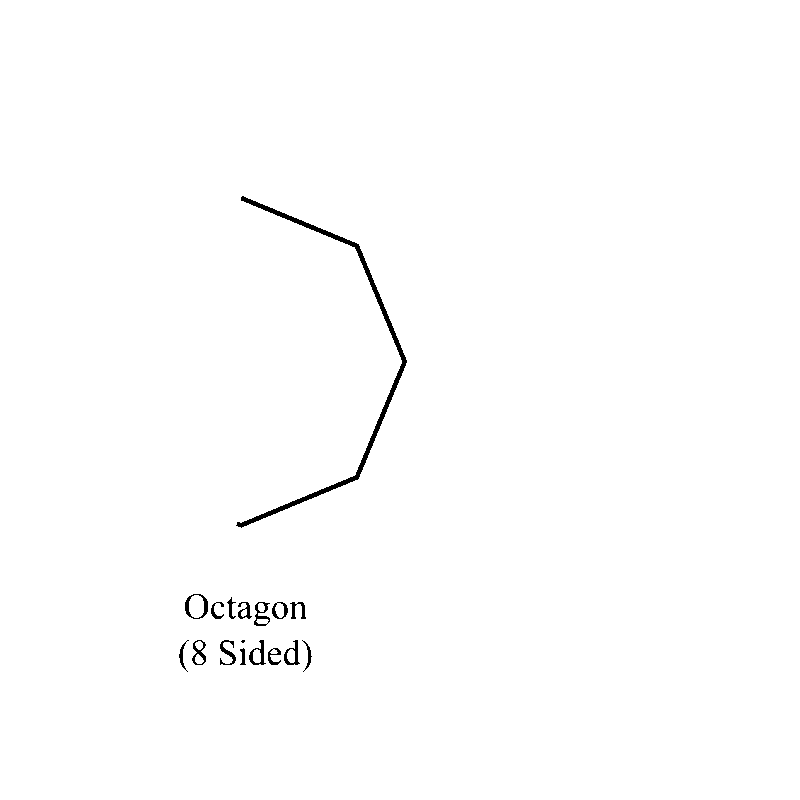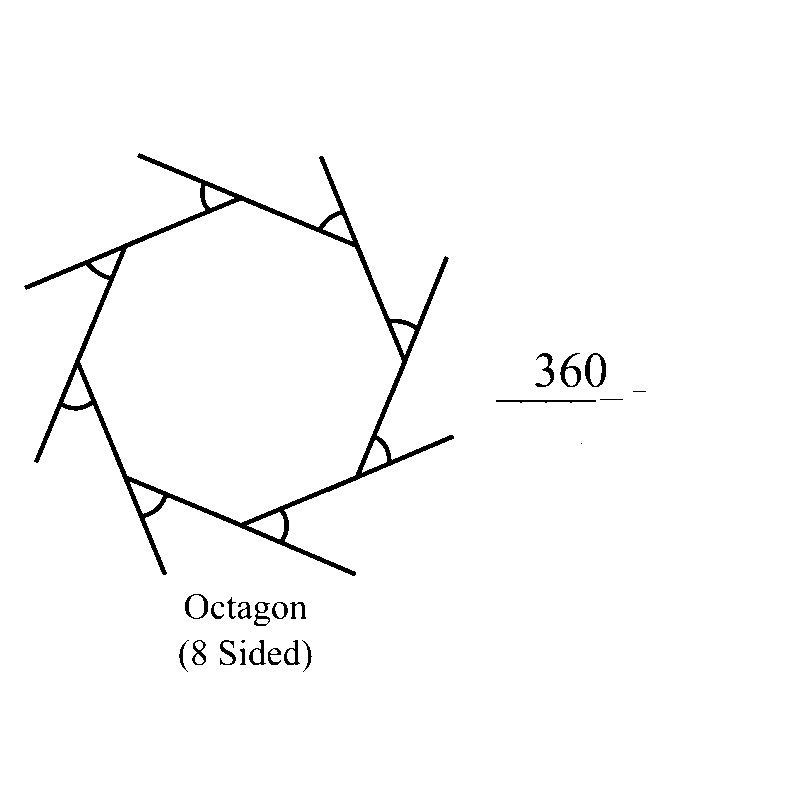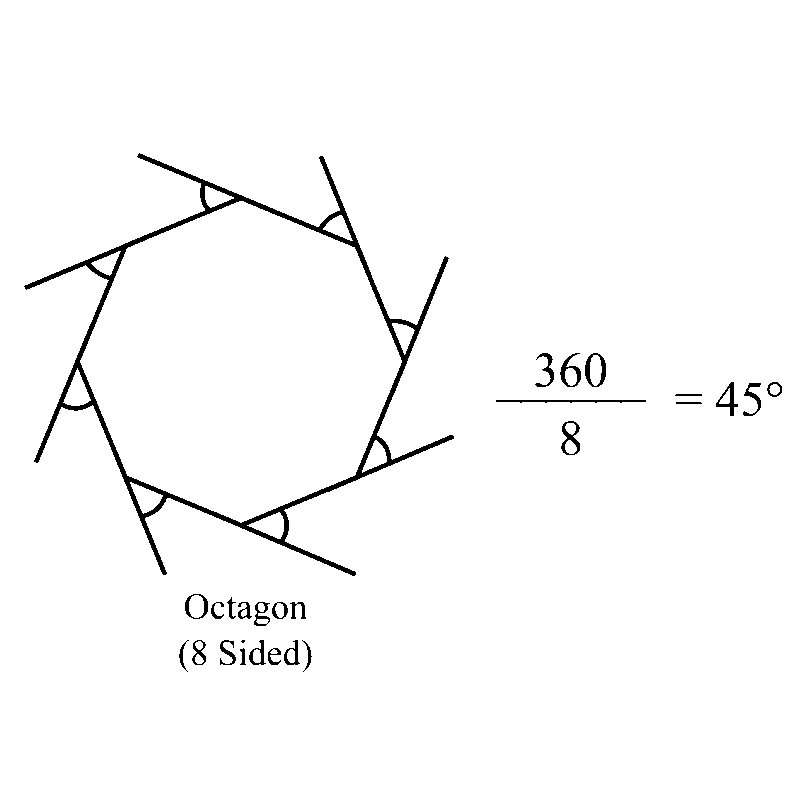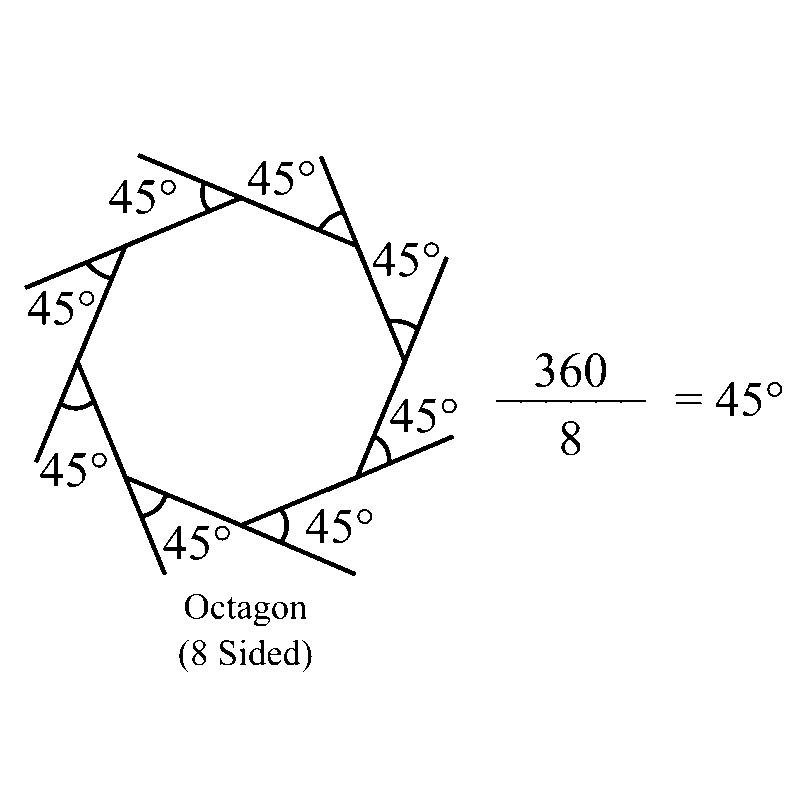
In short, an exterior angle for an n-sided shape can be calculated by simply dividing 360 degrees by n.
Applications of Calculating the Measure of an Exterior Angle
Calculating the measure of an exterior angle is a fundamental concept in geometry that has various practical applications across different fields. Here are some key applications:Measure Of An Exterior Angle
1. Architecture and Construction
Designing Structures: Architects and engineers use exterior angles to design and construct buildings and other structures. For example, when creating floor plans for polygonal structures, knowing the exterior angles ensures proper alignment and stability.Measure Of An Exterior Angle
Creating Roofs and Bridges: The calculation of exterior angles is crucial in the design of roofs and bridges, especially those with polygonal shapes, to ensure that all components fit together correctly.Measure Of An Exterior Angle
2. Urban Planning
Street Layouts: Urban planners use exterior angles to design street layouts and intersections. For example, when designing roundabouts or traffic circles, the angles between roads must be calculated accurately to ensure smooth traffic flow.Measure Of An Exterior Angle
Park and Garden Designs: In landscape architecture, exterior angles help in designing park layouts, garden paths, and other outdoor spaces with geometric patterns.Measure Of An Exterior Angle
3. Art and Design
Creating Geometric Art: Artists and graphic designers use exterior angles to create geometric patterns and artworks. Understanding the properties of polygons and their exterior angles helps in designing symmetrical and aesthetically pleasing pieces.Measure Of An Exterior Angle
Tiling and Mosaics: When designing tiling patterns or mosaics, the calculation of exterior angles ensures that the tiles fit together without gaps or overlaps, creating a seamless design.Measure Of An Exterior Angle
4. Navigation and Geography
Map Making: Cartographers use the principles of exterior angles in the creation of maps and navigation charts. Accurate calculation of angles is essential for representing geographical features and plotting courses.Measure Of An Exterior Angle
Surveying: Surveyors use exterior angles to measure and map out land boundaries and construction sites. This is crucial for creating accurate property maps and ensuring legal boundaries are maintained.Measure Of An Exterior Angle
5. Robotics and Animation
Programming Movement: In robotics, calculating exterior angles is essential for programming the movement of robots, especially those that navigate polygonal paths or need to make precise turns.Measure Of An Exterior Angle
Computer Animation: Animators use exterior angles in computer graphics to create realistic movements and rotations of objects. This is especially important in creating lifelike animations and simulations.Measure Of An Exterior Angle
6. Mathematics Education
- Teaching Geometry: Calculating exterior angles is a fundamental topic in geometry education. It helps students understand the properties of polygons and improves their problem-solving skills.Measure Of An Exterior Angle
Exterior Angles of Regular Polygons
-
Q: What is the formula to find the measure of an exterior angle of a regular polygon?
A: The formula is , where is the number of sides. -
Q: What is the measure of an exterior angle of a regular triangle?
A: 120° -
Q: What is the measure of an exterior angle of a regular quadrilateral?
A: 90° -
Q: What is the measure of an exterior angle of a regular pentagon?
A: 72° -
Q: How do you find the number of sides of a regular polygon if the measure of an exterior angle is 40°?
A: -
Q: What is the sum of the exterior angles of any polygon?
A: 360° -
Q: What is the measure of each exterior angle of a regular hexagon?
A: 60° -
Q: If a regular polygon has 12 sides, what is the measure of each exterior angle?
A: 30° -
Q: What is the relationship between an interior angle and an exterior angle in a regular polygon?
A: They are supplementary. -
Q: What is the measure of an exterior angle of a regular octagon?
A: 45° -
Q: What is the measure of an exterior angle of a regular decagon?
A: 36° -
Q: If the exterior angle of a regular polygon is 24°, how many sides does it have?
A: -
Q: What is the measure of an exterior angle of a regular dodecagon?
A: 30° -
Q: What is the sum of the measures of all exterior angles of a regular hexagon?
A: 360° -
Q: What is the exterior angle of a regular polygon with 20 sides?
A: 18° -
Q: Can the measure of an exterior angle of a regular polygon be less than 10°?
A: Yes, if the polygon has more than 36 sides. -
Q: What is the measure of an exterior angle of a regular heptagon?
A: ≈ 51.43° -
Q: If a regular polygon has an exterior angle of 15°, how many sides does it have?
A: 24 -
Q: What is the exterior angle of a regular polygon with 50 sides?
A: 7.2° -
Q: What is the exterior angle of a regular polygon with 25 sides?
A: 14.4° -
Q: If the measure of an exterior angle of a regular polygon is 45°, how many sides does the polygon have?
A: 8 -
Q: What is the relationship between the number of sides of a regular polygon and the measure of its exterior angles?
A: As the number of sides increases, the measure of each exterior angle decreases. -
Q: What is the exterior angle of a regular polygon with 100 sides?
A: 3.6° -
Q: What is the exterior angle of a regular polygon with 8 sides?
A: 45° -
Q: Can a regular polygon have an exterior angle of 90°?
A: Yes, it would be a square (4 sides). -
Q: What is the exterior angle of a regular polygon with 7 sides?
A: ≈ 51.43° -
Q: What is the measure of each exterior angle of a regular nonagon?
A: 40° -
Q: If the exterior angle of a regular polygon is 10°, how many sides does it have?
A: 36 -
Q: What is the exterior angle of a regular polygon with 30 sides?
A: 12° -
Q: What is the measure of each exterior angle of a regular icosagon (20 sides)?
A: 18° -
Q: If the exterior angle of a regular polygon is 5°, how many sides does it have?
A: 72 -
Q: What is the exterior angle of a regular polygon with 15 sides?
A: 24° -
Q: What is the measure of each exterior angle of a regular tridecagon (13 sides)?
A: ≈ 27.69° -
Q: What is the exterior angle of a regular polygon with 6 sides?
A: 60° -
Q: Can a regular polygon have an exterior angle of 72°?
A: Yes, it would be a pentagon (5 sides). -
Q: What is the exterior angle of a regular polygon with 5 sides?
A: 72° -
Q: What is the measure of each exterior angle of a regular tetradecagon (14 sides)?
A: ≈ 25.71° -
Q: If the exterior angle of a regular polygon is 8°, how many sides does it have?
A: 45
Exterior Angles of Regular Polygons
-
Q: What is the measure of an exterior angle of a regular icosagon?
A: 18° -
Q: If the exterior angle of a regular polygon is 6°, how many sides does it have?
A: 60 -
Q: What is the measure of an exterior angle of a regular enneadecagon (19 sides)?
A: ≈ 18.95° -
Q: What is the measure of an exterior angle of a regular hendecagon (11 sides)?
A: ≈ 32.73° -
Q: What is the measure of an exterior angle of a regular hexadecagon (16 sides)?
A: 22.5° -
Q: If the exterior angle of a regular polygon is 9°, how many sides does it have?
A: 40 -
Q: What is the measure of an exterior angle of a regular tridecagon (13 sides)?
A: ≈ 27.69° -
Q: What is the measure of an exterior angle of a regular pentadecagon (15 sides)?
A: 24° -
Q: Can a regular polygon have an exterior angle of 180°?
A: No, because it would imply a polygon with 2 sides. -
Q: What is the measure of an exterior angle of a regular nonadecagon (19 sides)?
A: ≈ 18.95° -
Q: What is the measure of an exterior angle of a regular octadecagon (18 sides)?
A: 20° -
Q: If the exterior angle of a regular polygon is 7.2°, how many sides does it have?
A: 50 -
Q: What is the measure of an exterior angle of a regular hexagon (6 sides)?
A: 60° -
Q: If the exterior angle of a regular polygon is 22.5°, how many sides does it have?
A: 16 -
Q: What is the measure of an exterior angle of a regular tetradecagon (14 sides)?
A: ≈ 25.71° -
Q: If the exterior angle of a regular polygon is 27°, how many sides does it have?
A: 13 -
Q: What is the measure of an exterior angle of a regular dodecagon (12 sides)?
A: 30° -
Q: What is the measure of an exterior angle of a regular pentadecagon (15 sides)?
A: 24° -
Q: If the exterior angle of a regular polygon is 2°, how many sides does it have?
A: 180 -
Q: What is the measure of an exterior angle of a regular octadecagon (18 sides)?
A: 20° -
Q: What is the measure of an exterior angle of a regular nonagon (9 sides)?
A: 40° -
Q: If the exterior angle of a regular polygon is 45°, how many sides does it have?
A: 8 -
Q: What is the measure of an exterior angle of a regular heptagon (7 sides)?
A: ≈ 51.43° -
Q: What is the measure of an exterior angle of a regular decagon (10 sides)?
A: 36° -
Q: If the exterior angle of a regular polygon is 6°, how many sides does it have?
A: 60 -
Q: What is the measure of an exterior angle of a regular polygon with 9 sides?
A: 40° -
Q: What is the measure of an exterior angle of a regular polygon with 100 sides?
A: 3.6° -
Q: If the exterior angle of a regular polygon is 12°, how many sides does it have?
A: 30 -
Q: What is the measure of an exterior angle of a regular polygon with 25 sides?
A: 14.4° -
Q: What is the measure of an exterior angle of a regular polygon with 50 sides?
A: 7.2° -
Q: If the exterior angle of a regular polygon is 72°, how many sides does it have?
A: 5 -
Q: What is the measure of an exterior angle of a regular polygon with 10 sides?
A: 36° -
Q: If the exterior angle of a regular polygon is 24°, how many sides does it have?
A: 15 -
Q: What is the measure of an exterior angle of a regular polygon with 12 sides?
A: 30° -
Q: If the exterior angle of a regular polygon is 120°, how many sides does it have?
A: 3 -
Q: What is the measure of an exterior angle of a regular polygon with 6 sides?
A: 60° -
Q: If the exterior angle of a regular polygon is 18°, how many sides does it have?
A: 20 -
Q: What is the measure of an exterior angle of a regular polygon with 8 sides?
A: 45° -
Q: What is the measure of an exterior angle of a regular polygon with 5 sides?
A: 72°







