Loading [MathJax]/extensions/tex2jax.js

Finding the area under a curve using integration | Free (1)

Find the area under the curve f(x)= √(4-x^2 ) on the interval x=0 to x=2.
NUMBERS TUTORING INSTITUTES IN DUBAI

Finding the area under a curve using integration

Find the area under the curve f ( x ) = 4 − x 2 on the interval x=0 to x=2.

Solution:
To find the area, we need to integrate the function over this interval:

∫ 0 2   4 − x 2 d x
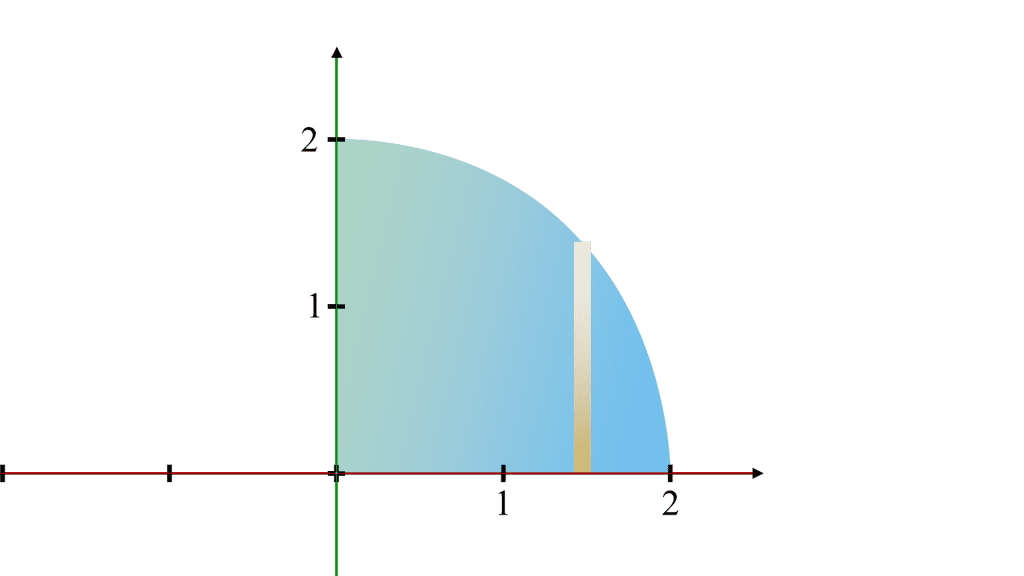
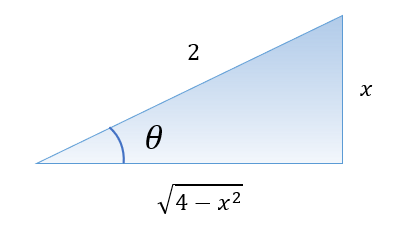
Finding the area under a curve using integration

There are two methods to solve this problem. Before we look at both methods, let’s look at the triangle below:

We’ll name the side opposite the angle θ as x, the side adjacent as a and the Hypotenuse as 2.

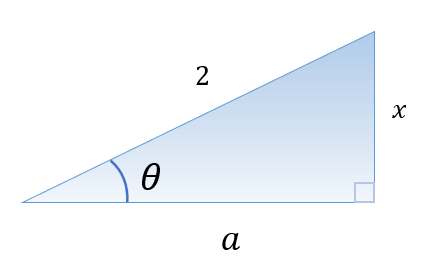
Finding the area under a curve using integration

Using the Pythagorean theorem, we’ll calculate the value of a in terms of x.

a 2 + x 2 = 2 2 a 2 + x 2 = 4 a 2 = 4 − x 2 a 2 = 4 − x 2 a = 4 − x 2

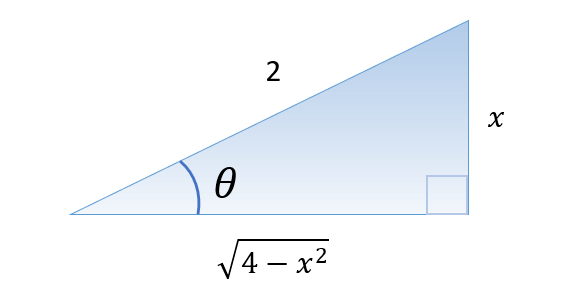
Finding the area under a curve using integration

Applying trig to the triangle above, we get:

sin ⁡ θ = x 2

Cross multiplying, we get:

x = 2 sin ⁡ θ ------- ①
cos ⁡ θ = 4 − x 2 2

Cross multiplying, we get :

4 − x 2 = 2 cos ⁡ θ ------ ②

We will now integrate, using METHOD 1.

∫ 0 2   4 − x 2 d x

By rewriting this integral in terms of θ. Using equation ② above, we can substitute 2 cos⁡θ for 4 − x 2 . The integral therefore becomes:

∫ 0 2   4 − x 2 d x = ∫ 0 2   2 cos ⁡ θ d x

We still have dx, which is in terms of x. Let’s use equation ① above to rewrite in terms of  θ. ---------------③

x=2sin⁡θx=2\sin\theta

Taking the derivative of both sides with respect to θ.

dxdθ=2cos⁡θ\frac{dx}{d\theta}=2\cos\theta

Multiplying both sides by dθ

d x = 2 cos ⁡ θ d θ − − − − − − ④

Substituting equation ④ into equation ③ we get:

= ∫ 0 2   2 cos ⁡ θ d x = ∫ 0 2   2 cos ⁡ θ ⋅ 2 cos ⁡ θ d θ = ∫ 0 2   4 cos 2 ⁡ θ d θ = 4 ∫ 0 2   cos 2 ⁡ θ d θ
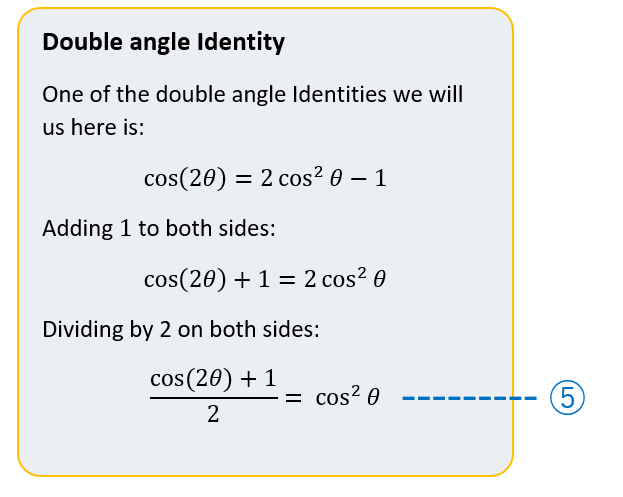
Finding the area under a curve using integration

Using equation ⑤ to the right, substitute into the equation above

= 4 ∫ 0 2 cos ⁡ ( 2 θ ) + 1 2 d θ = 4 2 ∫ 0 2 ( cos ⁡ ( 2 θ ) + 1 ) d θ = 2 ∫ 0 2 ( cos ⁡ ( 2 θ ) + 1 ) d θ = 2 [ ∫ 0 2 cos ⁡ ( 2 θ ) d θ + ∫ 0 2 1 d θ ]
Finding the area under a curve using integration
= 2 [ 1 2 sin ⁡ ( 2 θ ) + θ ] 0 2 − − − − − − ⑥  

We now need to rewrite the above expression in terms of x.

U s i n g s i n θ = x 2

Solving for θ we get

θ = sin − 1 ⁡ ( x 2 ) − − − − − − − − ⑦  

Substituting ⑦ above in to expression ⑥, we get:

= 2 [ 1 2 sin ⁡ ( 2 sin − 1 ⁡ ( x 2 ) + sin − 1 ⁡ ( x 2 ) ] 0 2 = 2 [ ( 1 2 sin ⁡ ( 2 sin − 1 ⁡ ( 2 2 ) + sin − 1 ⁡ ( 2 2 ) ) − ( 1 2 sin ⁡ ( 2 sin − 1 ⁡ ( 0 2 ) + sin − 1 ⁡ ( 0 2 ) ) ] = 2 [ ( 1 2 sin ⁡ ( 2 sin − 1 ⁡ ( 1 ) ) + sin − 1 ⁡ ( 1 ) ) − ( 1 2 sin ⁡ ( 2 sin − 1 ⁡ ( 0 ) + sin − 1 ⁡ ( 0 ) ) ] = 2 [ ( 1 2 sin ⁡ ( 2 π 2 ) + π 2 ) − ( 1 2 sin ⁡ ( 2 ( 0 ) ) + 0 ) ] = 2 [ ( 1 2 sin ⁡ ( π ) + π 2 ) − ( 1 2 ( 0 ) + 0 ) ] = 2 [ ( 1 2 ( 0 ) + π 2 ) − ( 0 ) ] = 2 [ ( π 2 ) ] = π

Integrating using METHOD 2. In this method, we will use one of the formulas of integration, which is:

∫ a 2 − x 2 d x = x 2 a 2 − x 2 + a 2 2 sin − 1 ⁡ x a + c

Let’s now integrate our function:

∫ 4 − x 2 d x ∫ 0 2 a 2 − x 2 d x = [ x 2 a 2 − x 2 + a 2 2 sin − 1 ⁡ ( x a ) ] ∫ 0 2 2 2 − x 2 d x = [ x 2 2 2 − x 2 + 2 2 2 sin − 1 ⁡ ( x 2 ) ] ∫ 0 2 2 2 − x 2 d x = [ x 2 2 2 − x 2 + 2 2 2 sin − 1 ⁡ ( x 2 ) ] 0 2 ∫ 0 2 2 2 − x 2 d x = [ ( 2 2 2 2 − 2 2 + 2 2 2 sin − 1 ⁡ ( 2 2 ) ) − ( 0 2 2 2 − 0 2 + 2 2 2 sin − 1 ⁡ ( 0 2 ) ) ] = [ ( 1 0 + 2 sin − 1 ⁡ ( 1 ) ) − ( 0 ⋅ 4 − 0 + 2 sin − 1 ⁡ ( 0 2 ) ) ] = [ ( 0 + 2 ⋅ ( π 2 ) ) − ( 0 + 0 ) ] = π

METHOD 3 is the same as Method 1, except for the first few steps.

Let’s look at the triangle again and recall that  x=2 sin⁡θ

Finding the area under a curve using integration
∫ 0 2   4 − x 2 d x

We’ll substitute x=2 sin⁡θ into the equation above:

∫ 0 2 4 − ( 2 sin ⁡ θ ) 2 d x = ∫ 0 2 4 − 4 sin 2 ⁡ θ d x  

Factor out the 4, inside the radical:

= ∫ 0 2   4 ( 1 − sin 2 ⁡ θ ) d x

Using the Pythagorean Trig. Identity:

sin 2 ⁡ θ + cos 2 ⁡ θ = 1

We can rearrange and end up with 1−sin⁡2θ=cos⁡2θ1-\sin^2\theta=\cos^2\theta , which we will substitute into the integral:

= ∫ 0 2   4 ( cos 2 ⁡ θ ) d x

The integral simplifies to:

= ∫ 0 2   2 cos ⁡ θ d x

If you go back to Method 1, earlier in this document, you will see the continuation of this problem being solved from this last step.

See More Blogs for Free

Wikipedia Link

Applications of Finding the Area Under a Curve Using Integration

Calculating the area under a curve using integration is a fundamental technique in calculus with numerous practical applications across various fields. Here are some key applications:

Finding the area under a curve using integration

2. Economics

  • Consumer and Producer Surplus: Integration is used to calculate the consumer surplus and producer surplus in a market. The consumer surplus is the area between the demand curve and the price level, while the producer surplus is the area between the supply curve and the price level.

    Finding the area under a curve using integration

  • Total Cost and Revenue: Economists use integration to determine the total cost and total revenue by integrating the marginal cost and marginal revenue functions, respectively.

    Finding the area under a curve using integration

3. Biology

  • Population Growth: Integration can be used to model population growth. By integrating the rate of population growth over time, biologists can estimate the total population at a given time.

    Finding the area under a curve using integration

4. Engineering

  • Area and Volume Calculations: Engineers use integration to find the area and volume of various shapes and objects. For instance, the area under a stress-strain curve helps determine the energy absorbed by a material before failure.

    Finding the area under a curve using integration

  • Center of Mass and Centroid: The center of mass and centroid of an object can be found by integrating the mass distribution or density function over the object’s volume or area.

    Finding the area under a curve using integration

5. Medicine

  • Pharmacokinetics: In pharmacokinetics, the area under the curve (AUC) of a drug concentration vs. time graph helps determine the drug’s bioavailability and the total exposure of the organism to the drug.

    Finding the area under a curve using integration

6. Environmental Science

  • Pollutant Dispersion: Environmental scientists use integration to calculate the total amount of a pollutant over a region or time period, which helps in assessing the environmental impact and designing remediation strategies.

    Finding the area under a curve using integration

author avatar
NUM8ERS
See Full Bio

More Sly academy Content