Sorting: Mastering Selection Sort and Insertion Sort in ArrayLists
Introduction to Sorting
Sorting is a fundamental operation in computer science, used to organize data in ascending or descending order. Sorting simplifies searching, data visualization, and processing tasks, making it a vital skill for developers. In this article, we will focus on two basic but powerful sorting algorithms: Selection Sort and Insertion Sort, both applied to Java ArrayLists. These methods form the building blocks for more advanced sorting techniques.
What is Sorting?
Sorting involves arranging elements in a specific order, typically ascending. For example, given an ArrayList of integers [4, 2, 8, 1, 5], sorting would result in [1, 2, 4, 5, 8]. While there are many sorting algorithms, each with unique strengths, this article focuses on two essential algorithms: Selection Sort and Insertion Sort.
Determining Whether an ArrayList is Already Sorted
Before sorting, it is often useful to check whether the ArrayList is already sorted. The following algorithm verifies if the elements in an ArrayList are in ascending order:
Implementation:
/** Checks if an ArrayList is sorted in ascending order */
public static boolean isSorted(ArrayList<Integer> array) {
for (int i = 0; i < array.size() - 1; i++) {
if (array.get(i + 1) < array.get(i)) {
return false; // Elements are out of order
}
}
return true;
}This method iterates through the ArrayList, comparing adjacent elements. If any pair of elements is out of order, it immediately returns false.
Selection Sort
Selection Sort divides the ArrayList into two parts: the sorted and unsorted subarrays. It repeatedly selects the smallest element from the unsorted portion and places it at the beginning of the sorted portion.
How It Works:
Identify the smallest element in the unsorted portion.
Swap it with the first unsorted element.
Repeat until the entire ArrayList is sorted.
Implementation:
/** Performs selection sort on an ArrayList */
public static ArrayList<Integer> selectionSort(ArrayList<Integer> array) {
for (int i = 0; i < array.size() - 1; i++) {
int smallestIndex = i;
int smallestElement = array.get(i);
for (int j = i + 1; j < array.size(); j++) {
if (array.get(j) < smallestElement) {
smallestIndex = j;
smallestElement = array.get(j);
}
}
// Swap the smallest element with the first unsorted element
if (smallestIndex > i) {
int temp = array.get(i);
array.set(i, smallestElement);
array.set(smallestIndex, temp);
}
}
return array;
}Insertion Sort
Insertion Sort builds the sorted portion of the ArrayList one element at a time by inserting each new element into its correct position within the sorted portion.
How It Works:
Assume the first element is already sorted.
Pick the next element and insert it into the correct position in the sorted portion.
Repeat until all elements are sorted.
Implementation:
/** Performs insertion sort on an ArrayList */
public static ArrayList<Integer> insertionSort(ArrayList<Integer> array) {
for (int i = 1; i < array.size(); i++) {
int currentElement = array.get(i);
int currentIndex = i;
for (int j = i; j > 0; j--) {
if (currentElement < array.get(j - 1)) {
// Shift the larger element to the right
array.set(j, array.get(j - 1));
array.set(j - 1, currentElement);
}
}
}
return array;
}Visualizing Selection Sort and Insertion Sort
Selection Sort starts by dividing the ArrayList into sorted and unsorted portions. It continuously selects the smallest element from the unsorted portion and places it in its correct position.
Insertion Sort works similarly but focuses on maintaining a sorted portion by inserting each new element in the correct place. This method is particularly efficient for small or partially sorted datasets.
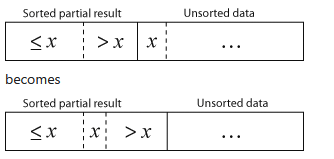
Runtime Comparisons
The efficiency of sorting algorithms is often evaluated using runtime complexity. Informal runtime comparisons between Selection Sort and Insertion Sort reveal important insights:
Selection Sort:
Time Complexity: O(n²)
Requires more data comparisons and swaps, making it slower for larger datasets.
Insertion Sort:
Time Complexity: O(n²)
More efficient than Selection Sort for small or partially sorted datasets.
Applications of Sorting
Sorting has a wide range of practical applications, including:
Data Organization:
Arranging student grades, product prices, or customer names in ascending order.
Search Optimization:
Binary search requires sorted data to function efficiently.
Improving Data Presentation:
Enhancing user interfaces by displaying sorted information.
Tips for Optimizing Sorting
Choose the Right Algorithm:
Use Insertion Sort for small or nearly sorted datasets.
Consider more advanced algorithms like Merge Sort or Quick Sort for larger datasets.
Minimize Swaps:
Optimize swap operations to reduce runtime.
Use Built-In Methods:
Java’s
Collections.sort()orArrays.sort()provide optimized sorting implementations.
Conclusion
Sorting is an essential tool in programming, enabling efficient data organization and retrieval. By understanding Selection Sort and Insertion Sort, you gain a solid foundation for tackling more complex algorithms in the future.
50 Highly Trending FAQs About Sorting with Detailed Answers
1. What is Sorting in Computer Science?
Sorting is the process of arranging elements in a specific order, either ascending or descending, based on certain criteria.
2. Why is Sorting Important?
Sorting improves data organization, makes searching more efficient, and is a fundamental operation in many algorithms.
3. What Are the Types of Sorting Algorithms?
Comparison-Based: Bubble Sort, Quick Sort, Merge Sort.
Non-Comparison-Based: Counting Sort, Radix Sort, Bucket Sort.
4. What is Bubble Sort?
Bubble Sort repeatedly swaps adjacent elements if they are in the wrong order. It is simple but inefficient for large datasets.
5. How to Implement Bubble Sort in Python?
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]6. What is Selection Sort?
Selection Sort repeatedly selects the smallest (or largest) element from the unsorted part and places it at the beginning.
7. What is the Time Complexity of Bubble Sort?
The time complexity of Bubble Sort is O(n²) in the worst and average cases.
8. What is Insertion Sort?
Insertion Sort builds a sorted list one element at a time by comparing and inserting elements into their correct position.
9. How to Implement Insertion Sort in Java?
void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}10. What is Merge Sort?
Merge Sort is a divide-and-conquer algorithm that splits an array into halves, recursively sorts them, and merges the sorted halves.
11. What is the Time Complexity of Merge Sort?
Merge Sort has a time complexity of O(n log n) for all cases (worst, average, best).
12. How to Implement Merge Sort in Python?
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
merge_sort(left)
merge_sort(right)
i = j = k = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
arr[k] = left[i]
i += 1
else:
arr[k] = right[j]
j += 1
k += 1
while i < len(left):
arr[k] = left[i]
i += 1
k += 1
while j < len(right):
arr[k] = right[j]
j += 1
k += 113. What is Quick Sort?
Quick Sort uses a pivot to partition the array into two halves, sorting them recursively. It is efficient for large datasets.
14. What is the Time Complexity of Quick Sort?
Best and Average Case: O(n log n)
Worst Case: O(n²), when the pivot is poorly chosen.
15. How to Implement Quick Sort in Java?
void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}16. What is Heap Sort?
Heap Sort is a comparison-based sorting algorithm that builds a heap data structure and extracts the maximum element repeatedly.
17. What is Counting Sort?
Counting Sort is a non-comparison-based algorithm that counts the occurrences of each element and uses this information to sort the array.
18. What is the Time Complexity of Counting Sort?
The time complexity of Counting Sort is O(n + k), where k is the range of the input.
19. What is Radix Sort?
Radix Sort processes digits of numbers from the least significant to the most significant, sorting at each step using a stable sorting algorithm like Counting Sort.
20. What is the Best Sorting Algorithm for Small Datasets?
Insertion Sort or Selection Sort is often preferred for small datasets due to their simplicity and low overhead.
21. What is the Best Sorting Algorithm for Large Datasets?
Merge Sort or Quick Sort is commonly used for large datasets because of their efficient time complexity.
22. What is Bucket Sort?
Bucket Sort distributes elements into buckets, sorts each bucket individually, and then concatenates them to form the sorted array.
23. What is Shell Sort?
Shell Sort is a generalization of Insertion Sort that allows elements to be moved farther apart to improve efficiency.
24. What is TimSort?
TimSort is a hybrid sorting algorithm derived from Merge Sort and Insertion Sort. It is used in Python’s and Java’s standard libraries.
25. What is Stable Sorting?
Stable Sorting preserves the relative order of equal elements. Examples include Merge Sort and Bubble Sort.
26. What is Unstable Sorting?
Unstable Sorting may change the relative order of equal elements. Examples include Quick Sort and Heap Sort.
27. What is External Sorting?
External Sorting is used for large datasets that cannot fit into memory. It involves dividing data into chunks, sorting them, and merging the results.
28. How to Sort Strings Alphabetically?
Use in-built methods:
Arrays.sort(stringArray);29. What is Hybrid Sorting?
Hybrid Sorting combines two or more sorting algorithms to leverage their strengths. TimSort is an example of hybrid sorting.
30. What is Natural Sorting?
Natural Sorting refers to the default ordering of elements, such as alphabetical for strings or ascending numerical order.
31. What is the Difference Between In-Place and Out-of-Place Sorting?
In-Place Sorting: Sorts the data within the same memory space (e.g., Quick Sort).
Out-of-Place Sorting: Requires additional memory (e.g., Merge Sort).
32. What is the Difference Between Internal and External Sorting?
Internal Sorting: Sorting within memory.
External Sorting: Sorting using external storage for large datasets.
33. How to Sort an ArrayList in Java?
Collections.sort(arrayList);34. What is Dual-Pivot Quick Sort?
Dual-Pivot Quick Sort uses two pivots instead of one, reducing comparisons and improving efficiency.
35. What is the Role of Comparator in Sorting?
A Comparator allows custom sorting by defining a comparison function:
Collections.sort(list, (a, b) -> a.compareTo(b));36. What is Three-Way Partitioning in Quick Sort?
Three-way partitioning divides the array into three parts: less than, equal to, and greater than the pivot.
37. What is Pancake Sorting?
Pancake Sorting flips subsets of the array to bring the largest element to the front iteratively.
38. What is Gnome Sort?
Gnome Sort rearranges misplaced elements by repeatedly swapping them into their correct positions.
39. What is BogoSort?
BogoSort randomly shuffles the array until it is sorted. It is highly inefficient and used for educational purposes.
40. What is Cycle Sort?
Cycle Sort rearranges elements by moving them directly to their correct positions, minimizing writes.
41. How to Sort Multidimensional Arrays?
Use custom comparators or sorting logic:
Arrays.sort(arr, (a, b) -> Integer.compare(a[0], b[0]));42. How to Check If an Array is Already Sorted?
boolean isSorted = IntStream.range(0, arr.length - 1).allMatch(i -> arr[i] <= arr[i + 1]);43. How to Sort in Descending Order?
Arrays.sort(arr, Collections.reverseOrder());44. What is the Space Complexity of Merge Sort?
Merge Sort has a space complexity of O(n) due to the temporary arrays used during merging.
45. What is Lazy Sorting?
Lazy Sorting delays sorting until a certain point, optimizing performance for operations that do not require fully sorted data.
46. How to Perform Partial Sorting?
Sort only a subset of the array:
Arrays.sort(arr, 0, k);47. What is Patience Sorting?
Patience Sorting is a technique used to find the longest increasing subsequence in O(n log n) time.
48. What is Bitonic Sort?
Bitonic Sort is a parallel sorting algorithm that works by creating bitonic sequences and merging them.
49. What is Odd-Even Sort?
Odd-Even Sort compares and swaps adjacent elements in alternating passes to sort the array.
50. What is the Role of Stable Sorting in Real-World Applications?
Stable Sorting is crucial for maintaining the original order of equivalent elements, especially in multi-level sorting scenarios like database queries.








