9.10 Electrolysis and Faraday’s Law

Introduction to Electrolysis and Faraday’s Law

Congratulations! You’ve reached the final topic of AP Chemistry. Throughout this journey, we’ve explored acids, bases, equilibrium, thermodynamics, and now our last section focuses on the power of electricity in driving nonspontaneous redox reactions using electrolytic cells. Additionally, we’ll discuss Faraday’s Law and how to solve related electrolysis problems.

Electrolytic Cells: A Quick Recap 🔋

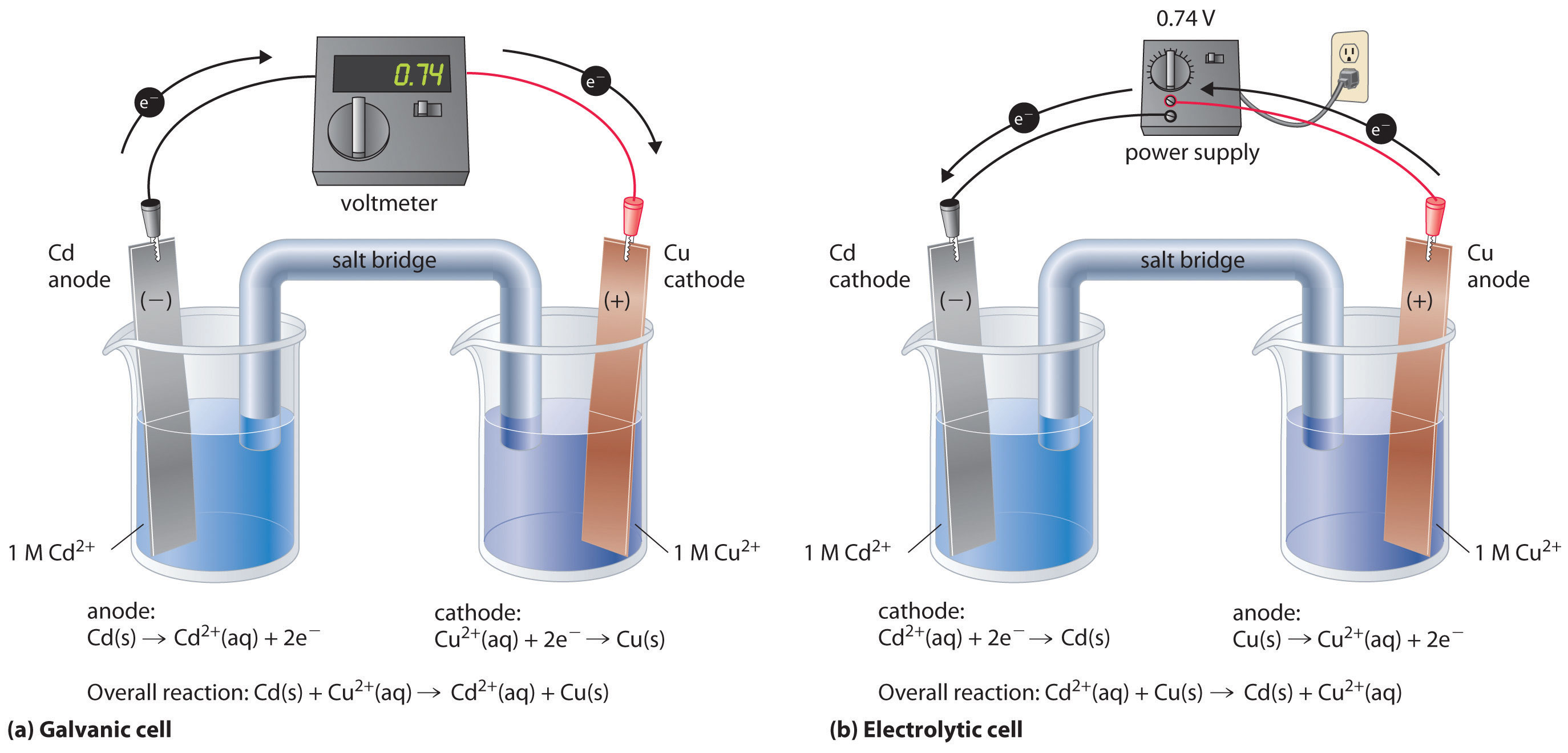
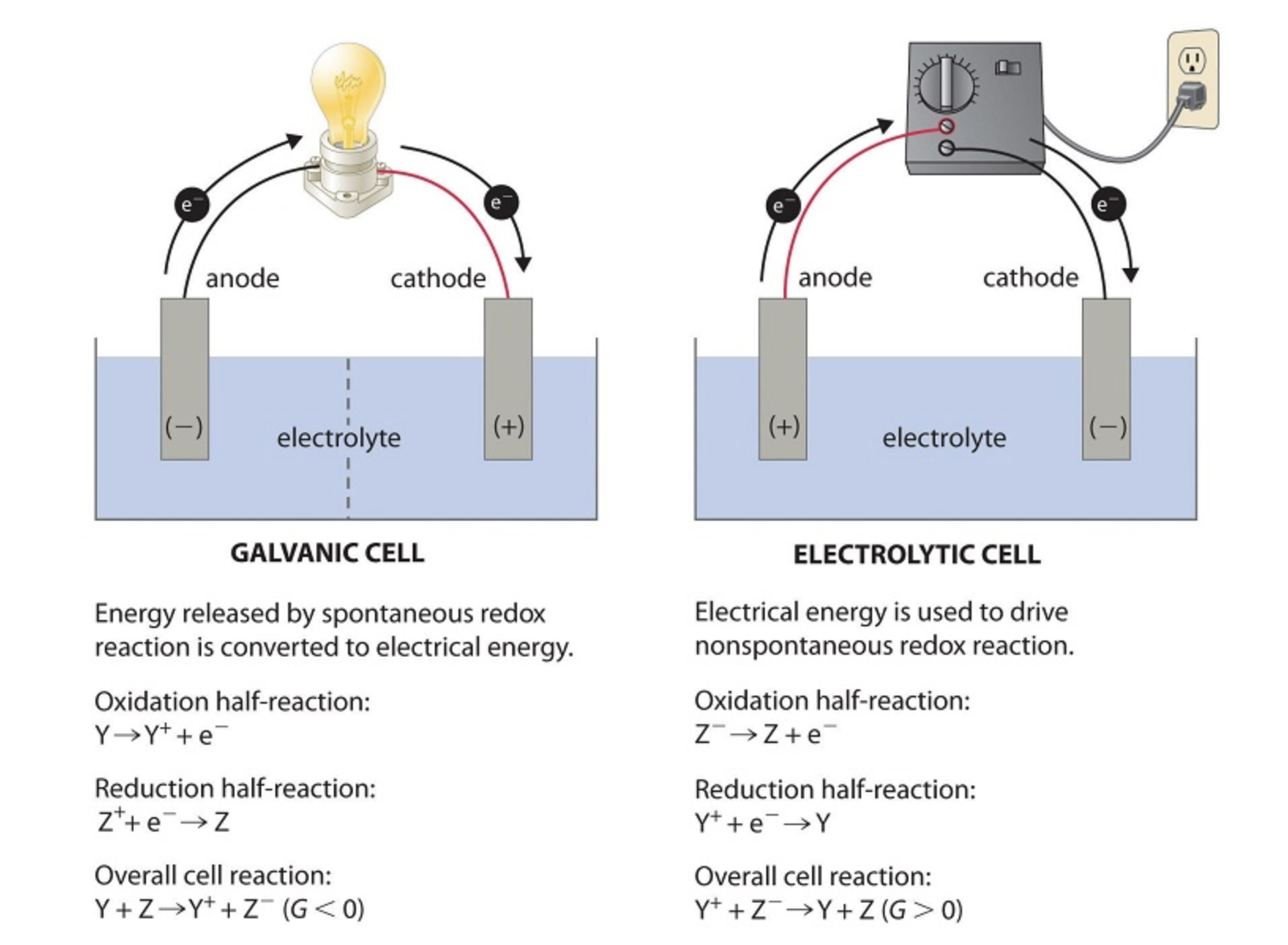
Electrolytic cells require an external energy source, like a battery, to drive nonspontaneous redox reactions. This distinguishes them from galvanic (or voltaic) cells, which produce electricity through spontaneous reactions.

In an electrolytic cell:

• Oxidation (loss of electrons) occurs at the anode.
• Reduction (gain of electrons) occurs at the cathode.
• Electrons are pushed from the anode to the cathode via an external power source.

Example of an Electrolytic Cell

Consider a cell involving copper (Cu) and zinc (Zn):

1. Electrons are pumped from Cu, forming Cu²⁺, and are transferred to Zn²⁺, forming Zn metal.
2. The reaction occurring is: $$\text{Cu} + \text{Zn}^{2+} \rightarrow \text{Cu}^{2+} + \text{Zn}$$
   
3. Using standard reduction potentials, the cell potential (Ecell) is calculated as -1.10 V, indicating a nonspontaneous reaction. To make it occur, a battery with a voltage ≥ 1.10 V is needed.

Key Comparison: Electrolytic vs. Galvanic Cells

• Galvanic cells generate electrical energy from spontaneous reactions, while electrolytic cells require an external power source to drive nonspontaneous reactions.
• Electrons flow from the anode to the cathode in both cells.
• Oxidation occurs at the anode and reduction occurs at the cathode in both cell types.

Faraday’s Law of Electrolysis

Faraday’s Law enables the calculation of mass changes at electrodes during electrolysis by relating current, time, and the number of electrons transferred in a reaction. The key formula is:

$$I = \frac{q}{t}$$

Where:

• I = current (amperes)
• q = charge (coulombs)
• t = time (seconds)

Faraday’s Constant (F) relates moles of electrons to charge:

$$F = 96,485 \, \text{C/mol e-}$$

Solving Electrolysis Problems with Faraday’s Law

Example Problem: Calculate the mass of chromium produced when Cr(NO₃)₂ is electrolyzed for 60 minutes at a current of 15 A.

1. Convert time to seconds: $$60 \, \text{min} \times 60 \, \text{s/min} = 3,600 \, \text{s}$$
   
2. Calculate total charge: $$q = I \times t = 15 \, \text{A} \times 3,600 \, \text{s} = 54,000 \, \text{C}$$
   
3. Convert charge to moles of electrons: $$\text{Moles of e-} = \frac{q}{F} = \frac{54,000 \, \text{C}}{96,485 \, \text{C/mol}} = 0.559 \, \text{mol e-}$$
   
4. Use stoichiometry to find moles of chromium: $$\text{Moles of Cr} = 0.559 \, \text{mol e-} \times \left( \frac{1 \, \text{mol Cr}}{2 \, \text{mol e-}} \right) = 0.2795 \, \text{mol Cr}$$
   
5. Convert moles of chromium to grams (molar mass of Cr = 52.0 g/mol): $$\text{Mass of Cr} = 0.2795 \, \text{mol} \times 52.0 \, \text{g/mol} = 14.54 \, \text{g}$$
   

Result: 14.54 g of chromium is produced.

Electrolysis Problem-Solving Tips

• Identify the number of moles of electrons involved in the redox reaction.
• Use Faraday’s Constant for conversions.
• Apply dimensional analysis to convert between charge, moles of electrons, and mass.

Practice Problem

Determine the time needed to produce 10 g of silver (Ag) in an electrolytic cell using a current of 5 A. (Molar mass of Ag = 107.87 g/mol)

Solution Strategy:

1. Convert mass to moles.
2. Relate moles to moles of electrons.
3. Calculate the total charge.
4. Use I = q / t to find time.