10.3 Interference and Superposition (Waves in Tubes and on Strings)

10.3 Interference and Superposition (Waves in Tubes and on Strings)

As of 2021, the College Board focuses only on Units 1-7 in the AP Physics 1 exam. However, this detailed exploration of interference and superposition is an excellent resource for understanding waves in tubes and on strings.

Enduring Understanding 6.D 💻

Interference and superposition lead to standing waves and beats.

Essential Knowledge:

• 6.D.1: Superposition occurs when two or more wave pulses interact to produce amplitude variations.

• 6.D.2: Traveling waves interacting with each other can alter the amplitude of the resultant wave.

• 6.D.3: Standing waves result from the interference of incident and reflected waves, featuring nodes (no motion) and antinodes (maximum motion).

• 6.D.4: Standing wave wavelengths depend on the size of the confined region.

• 6.D.5: Beats arise when waves of slightly different frequencies interfere, leading to periodic amplitude variations.

Superposition & Interference Patterns

When two or more waves overlap, their amplitudes combine (superposition). The resulting amplitude can be determined by adding the individual amplitudes of the waves at each point.

Key Types of Interference:

• Constructive Interference: Amplitudes add, increasing wave height.

• Destructive Interference: Amplitudes cancel, reducing wave height.

Once the waves pass through each other, they return to their original amplitudes. This phenomenon is crucial for understanding wave interactions in musical instruments and other systems.

Beats

Beats occur when two waves of nearly identical frequencies interfere. The resulting amplitude variations create a regular pattern of loudness.

Key Points:

• Beat frequency = Difference between the two wave frequencies.

• Lower beat frequency = Closer matching wave frequencies.

Beats are often used to tune musical instruments, as the periodic variations help identify frequency mismatches.

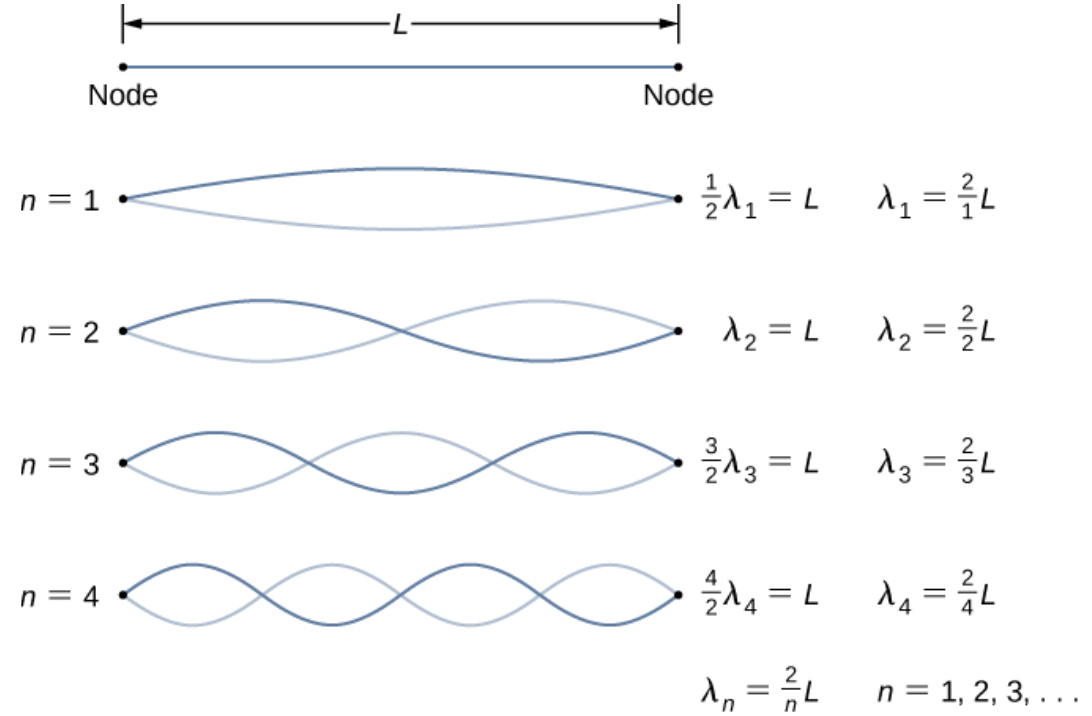
Standing Waves

Standing waves form when two waves of the same frequency and amplitude interfere. These waves appear stationary, with alternating regions of constructive and destructive interference.

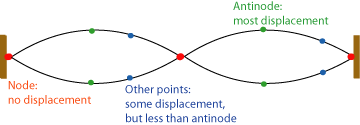
Components:

• Nodes: Points of zero motion.

• Antinodes: Points of maximum motion.

The simplest standing wave, called the fundamental, contains one antinode and two nodes. Higher frequencies create additional nodes and antinodes, known as harmonics.

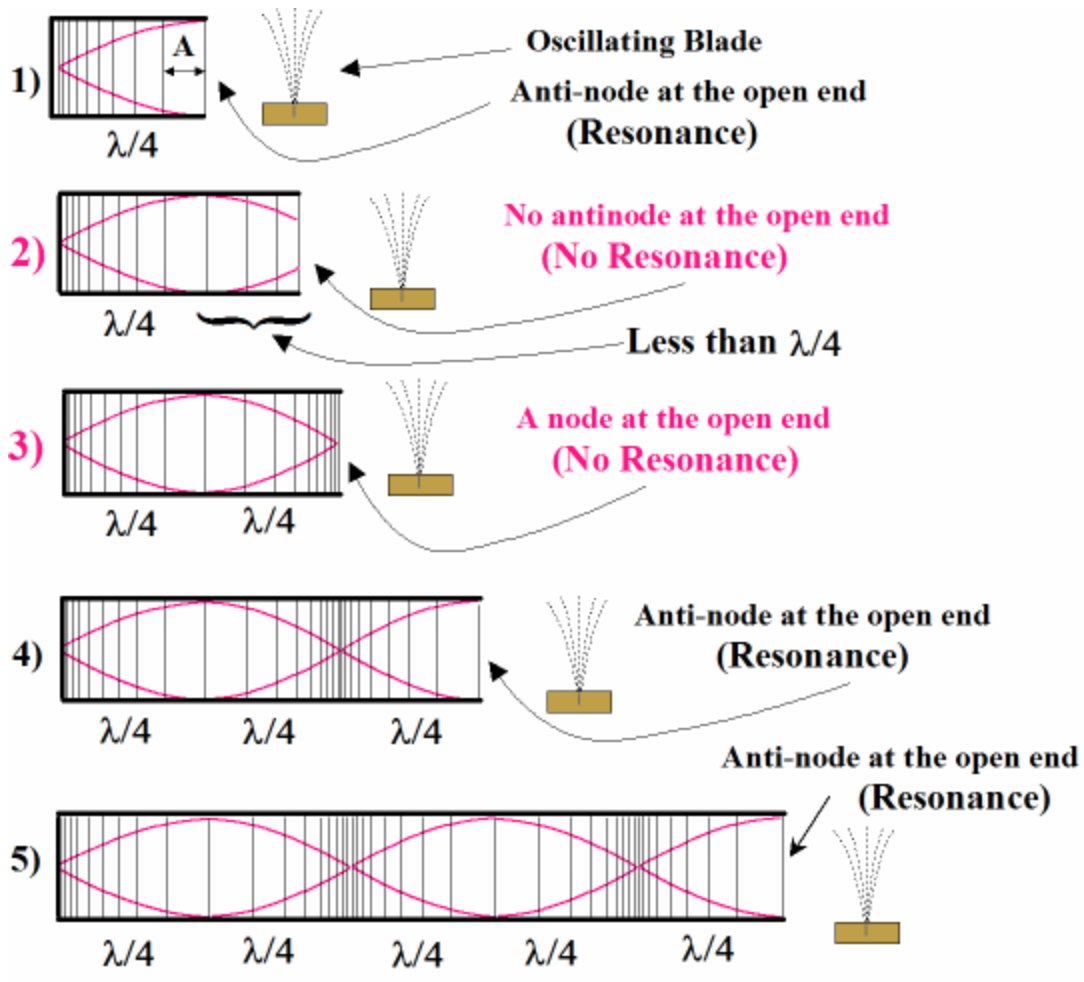
Waves in Tubes

Standing waves also form in tubes, providing the foundation for many musical instruments. By adjusting the tube’s length or the vibration frequency, different notes can be produced.

Types of Tubes:

1. Open-Open Tubes:

   • Antinodes at both ends.

   • Resonates at all harmonics.

2. Open-Closed Tubes:

   • Antinode at the open end and a node at the closed end.

   • Resonates only at odd harmonics.

Resonance occurs when the wave’s wavelength fits the tube length such that an antinode appears at the open ends.

Sample Questions

Example 1: Waves on a String

A string with length 1.20 m and linear density of is attached to a 120 Hz tuning fork. The standing wave pattern has four loops. Determine:

1. Wavelength: The length contains two complete waves, so .

2. Wave Speed: Using , .

3. Doubling the Loops: Decrease tension (lower ) to decrease the wavelength.

4. Amplitude: An antinode travels a total vertical distance of 4 cm, so amplitude = 1 cm.

Example 2: Waves in an Open Tube

A tuning fork vibrates at 512 Hz near an open tube resonating at its fundamental frequency. Given sound speed :

1. Length of Tube: for open-open tubes. Using , . Therefore, .

2. New Fundamental (Open-Closed): With , . Using , .

Key Takeaways

• Interference, superposition, and resonance explain many wave phenomena in strings and tubes.

• Beats result from frequency differences and are used for tuning.

• Standing waves depend on boundaries and are key to musical acoustics.