Maximizing Your SAT Prep with Effective Practice Test Strategies
Regular practice tests are a cornerstone of successful SAT preparation. They not only help you apply the strategies you’ve learned but also condition you for the test day environment. Here’s how to get the most out of your SAT practice tests.
Scheduling Practice Tests
- Frequency: Aim to take a full-length practice test every few weeks. This frequency helps you gauge your progress and refine your test-taking strategies under timed conditions.
- Timing: Ideally, schedule your practice tests on a Saturday or Sunday morning to mimic the actual test day conditions. Adhering to the official test timing is crucial to get a realistic feel for the pace and pressure of the SAT.
Utilizing Practice Tests
- Editions and Versions: Ensure you are using the most current practice tests available. For example, the second edition of some prep books includes three actual SATs, providing valuable, realistic practice material.
- Tracking Errors: Always mark the questions you get wrong. Add these to a collection of problems to revisit during your shorter study sessions. This approach helps you focus on areas where you need improvement and prevents making the same mistakes repeatedly.
Scoring and Reviewing
- Self-Scoring: After completing each test, score it yourself to get immediate feedback on your performance. Keep track of these scores in a journal or spreadsheet to monitor your improvement over time.
- Review Session: Dedicate time to review every incorrect answer. Understand why you chose the wrong option and what the correct answer is. This review is crucial for turning weaknesses into strengths.
Simulating Real Test Conditions
- Full-Length Practice: While it’s fine to focus on math sections initially, make sure to complete at least the last two practice tests in one sitting, covering all sections of the SAT. This helps build stamina and familiarity with the test’s length and complexity.
- Adding an Experimental Section: Consider adding an extra math section to some of your practice tests to simulate the experimental section found in the actual SAT. This additional section helps you practice managing your energy and focus throughout an extended testing period.
Essential Math Formulas to Memorize for the SAT
Preparing for the SAT involves more than just understanding concepts and practicing problems; it also requires you to memorize key formulas that are crucial for solving various mathematical questions efficiently. Here’s an updated guide to the math formulas you should have at your fingertips for the SAT.
Given Geometry Formulas
At the start of each SAT Math section, you are provided with a set of geometry formulas. While these are given, memorizing them can save you valuable time during the test. Here’s a list of the essential geometry formulas provided:
Area Formulas:
- Rectangle: Area = length × width
- Triangle: Area = ½ × base × height
- Circle: Area = π × radius²
Volume Formulas:
- Rectangular Solid: Volume = length × width × height
- Cylinder: Volume = π × radius² × height
Pythagorean Theorem:
- In a right triangle: , where is the hypotenuse.
Special Right Triangles:
- 45-45-90 Triangle: The legs are equal, and the hypotenuse is leg×2.
- 30-60-90 Triangle: The shortest leg is opposite the 30° angle, the length of the hypotenuse is twice the shortest leg, and the length of the longer leg is shortestleg×3.
Additional Formulas to Memorize
Beyond the given formulas, there are several other formulas that are not provided on the test but are essential for solving certain types of problems:
Algebraic Formulas:
- Quadratic Formula: for solving ax² + bx + c = 0.
- Slope Formula: for calculating the slope of a line between two points.
- Slope-Intercept Form: , where is the slope and is the y-intercept.
Function Formulas:
- Distance Formula: for the distance between two points.
- Midpoint Formula: for finding the midpoint of a line segment.
Probability and Statistics:
- Probability:
- Average (Mean):
- Fundamental Counting Principle: If there are n ways to do one thing, and m ways to do another, then there are ways to do both.
Mastering Basic Geometry and Statistical Formulas for the SAT
Understanding and memorizing key formulas is essential for success on the SAT math section. This guide covers some fundamental geometry and statistical formulas that you should know.
Basic Geometry Formulas
In addition to the formulas provided at the beginning of the SAT math section, you should also be familiar with these essential geometry calculations:
- Perimeter of a Rectangle: (where is length and is width)
- Perimeter of a Square: (where s is the length of one side)
- Area of a Square:
Example Problem: A square has an area of 25 square centimeters. What is the length of a side, in centimeters, of the square? Given , it follows that .
Percent Change Formula
This simple formula is crucial for solving problems involving increases or decreases in values:
- Percent Change: Percent Change=
Example Problem: Suppose that increases from 8 to 9. By what percent does increase?
- Original value = 8
- Change = 9 – 8 = 1 Percent Change=(81)×100=12.5% Thus, increases by 12.5%.
Statistical Measures
Understanding different ways to describe data sets is another key area on the SAT:
Average (Arithmetic Mean):
Median: The middle value when the numbers are arranged in increasing order. If there’s an even number of values, the median is the average of the two middle numbers.
Mode: The number that appears most frequently. There can be more than one mode if multiple numbers appear with the same highest frequency.
Range:
Example Problem: The graph (not shown here) represents the frequency distribution of a list of integers between 0 and 6. To find the arithmetic mean, median, mode, and range, you would analyze the provided data set, calculate each value based on definitions, and interpret the graphical data appropriately.
nderstanding Statistical Measures and Simple Probability on the SAT
To excel in the SAT math section, it’s crucial to understand how to handle real data sets and compute basic statistics such as mean, median, mode, range, and probability. Let’s break down each calculation with a sample data set.
Data Set Analysis
Consider the following data set: 0, 0, 0, 1, 3, 3, 3, 3, 4, 4, 5, 5, 5, 6, 6.
Arithmetic Mean (Average)
The arithmetic mean is calculated by summing all the values and then dividing by the number of values:
- Calculation
Step-by-step solution:
Calculate the numerator:
Calculate the denominator:
Compute the arithmetic mean:
Final result:
- Median
The median is the middle value in a data set ordered from least to greatest:
- Median Calculation: In our ordered list, the middle value (the 8th in this case) is 3.
Mode
The mode is the number that appears most frequently:
- Mode Calculation: The value 3 appears four times, more than any other number.
Range
The range is the difference between the highest and lowest values:
- Range Calculation:
Simple Probability
To calculate the probability of a specific event:
- Example Problem: Compute the probability of selecting an even number from the data set.
- Even numbers in the set: 0, 0, 0, 4, 4, 6, 6 (7 occurrences)
- Total numbers in the set = 15
- Probability =
Note: It’s important to recognize that some numbers (like 0) appear more frequently, affecting their individual probabilities. For instance, the probability of selecting a 0 is , while selecting a 1 is .
Converting Average to Sum
To find the sum from an average:
- Formula: Sum = Average × Number of values
- Example Problem: Suppose the average score of 20 tests is 88.
- Sum = 88 × 20 = 1760
Key SAT Math Concepts and Formulas
To excel in the SAT Math section, it’s essential to be comfortable with basic arithmetic, algebra, geometry, and line equations. Here’s a detailed breakdown of these concepts along with examples to help you understand and apply them on test day.
1. Arithmetic Mean with Additional Number
Problem Example: The average (arithmetic mean) of five numbers is 20. When a sixth number is added, the average of the six numbers is 30. What is the sixth number?
- Solution:
- Step 1: Calculate the sum of the first five numbers: .
- Step 2: Calculate the sum of all six numbers: .
- Step 3: Find the sixth number by subtracting the sum of the first five numbers from the sum of all six: .
- Answer: The sixth number is 80.
2. The Distributive Property
The distributive property is fundamental in algebra and is expressed as:
Examples:
3. Slope Formula
The slope of a line measures its steepness and is calculated using two points and with the formula:
A common mistake is to subtract the x-coordinates before the y-coordinates, so be careful with the order.
Example: Calculate the slope of the line that passes through and .
- Solution:
-
- Answer: The slope is .
Geometric Insight: To go from to , you move up 2 (rise) and right 3 (run), which confirms the slope .
4. Slope-Intercept Form of a Line
The slope-intercept form of a line’s equation is:
where:
- is the slope.
- is the -intercept, or the point where the line crosses the -axis ( ).
Example: Write the equation of a line with a slope of 3 that passes through the point .
- Solution: Since and , the equation is:
Special Cases of Line Equations
Horizontal Lines: A horizontal line has a slope of 0 and takes the form:
Example: The horizontal line passing through is .
Vertical Lines: A vertical line has an undefined slope and cannot be expressed in slope-intercept form. It is represented as:
Example: The vertical line passing through is .
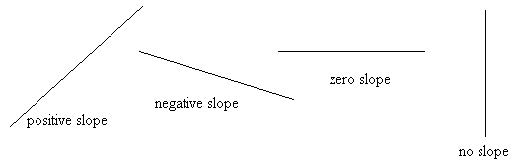
Slope and Line Direction:
- A positive slope means the line goes upward from left to right.
- A negative slope means the line goes downward from left to right.
- A zero slope corresponds to a horizontal line.
- Undefined slope (infinite slope) corresponds to a vertical line.
You should also know the following two facts:
Parallel lines have the same slope.
Perpendicular lines have slopes that are negative reciprocals of each other.
(10) You should know how to classify scatterplots on the SAT:
The following scatterplots show positive associations.

The scatterplot on the left shows a linear positive association, whereas the scatterplot on the right
shows a nonlinear positive association. The rightmost scatterplot looks like it might show an
exponential positive association.
Here are a few more scatterplots.

The leftmost scatterplot shows a nonlinear (possibly exponential) negative association, whereas
the other two show no association.
(11) Parallel lines cut by a tranversal:
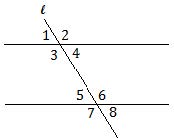
The figure above shows two parallel lines cut by the transversal l.
Angles 1, 4, 5, and 8 all have the same measure. Also, angles 2, 3, 6, and 7 all have the same
measure. Any two angles that do not have the same measure are supplementary, that is their
measures add to 180°.
(12) Two triangles are similar if their angles are congruent.
Note that similar triangles do not have to be the same size.
Also note that to show that two triangles are similar we need only show that two pairs of angles
are congruent. We get the third pair for free because all triangles have angle measures summing to
180 degrees.
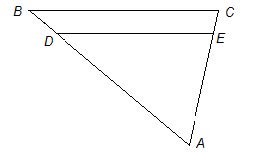
Understanding Similar Triangles and Basic Trigonometry
Similar Triangles
When analyzing geometric figures, it’s crucial to recognize when triangles are similar. This concept often appears on the SAT and can simplify complex problems.
Example Setup:
- Consider the figure where is parallel to .
- Alternate Interior Angles: Because is parallel to , angles and are congruent.
- Shared Angle: Triangles and share angle . Therefore, the two triangles are similar by the AA (Angle-Angle) similarity criterion.
Important Fact: Corresponding sides of similar triangles are proportional. This can be expressed as:
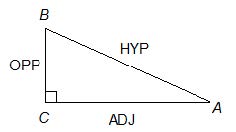
Basic Trigonometry of a Right Triangle
Understanding the relationships between angles and sides in right triangles is essential for solving trigonometric problems on the SAT.
- Hypotenuse: The side opposite the right angle. It is the longest side in the triangle.
- Legs: The other two sides. Their designation (opposite or adjacent) depends on the reference angle.
Three Basic Trig Functions:
- Sine (sin) of angle :
- Cosine (cos) of angle :
- Tangent (tan) of angle :
Example Problem
Given a right triangle, compute the three basic trigonometric functions for each angle (excluding the right angle).
Identify the sides relative to angle :
- Hypotenuse: The side opposite the right angle.
- Opposite: The side opposite angle .
- Adjacent: The side next to angle , but not the hypotenuse.
Calculate the Trig Functions:
- Sine:
- Cosine:
- Tangent:
Trigonometric Functions for Angles and
Given:
Explanation
Right Triangle Setup:
- Assume a right triangle with angles , , and the right angle.
- The hypotenuse has a length of 13 units.
- The legs opposite and adjacent to angles and are 12 units and 5 units, respectively.
Trigonometric Functions:
For angle :
- Sine ( ) is the ratio of the opposite side to the hypotenuse:
- Cosine ( ) is the ratio of the adjacent side to the hypotenuse:
- Tangent ( ) is the ratio of the opposite side to the adjacent side:
For angle (the complementary angle to ):
- Sine ( ) is the ratio of the opposite side (which is adjacent to ) to the hypotenuse:
- Cosine ( ) is the ratio of the adjacent side (which is opposite to ) to the hypotenuse:
- Tangent ( ) is the ratio of the opposite side to the adjacent side:
1. Cofunction Identities for Trigonometric Functions
Cofunction identities are particularly useful when dealing with complementary angles in trigonometric problems. They describe the relationship between sine and cosine functions for angles that add up to 90° (or radians).
Cofunction Identities:
Example Problem: Given a right triangle with one angle measuring x∘ where , find .
Solution:
Explanation:
Since the angles in a right triangle sum up to 180°, and one of the angles is always 90°, the remaining two angles are complementary (add up to 90°). Therefore, the sine of one angle is equal to the cosine of its complement, as demonstrated in the example.
2. Complex Numbers
A complex number has the form , where:
- is the real part.
- is the imaginary part.
- is the imaginary unit, defined as .
Examples of Complex Numbers:
- (since )
- (a pure imaginary number)
- (a real number)
- (zero)
Explanation:
- Real Numbers: When , the complex number is purely real (e.g., .
- Pure Imaginary Numbers: When , the complex number is purely imaginary (e.g., ).
- Zero: When both and , the complex number is simply zero.


Advanced Formula: The Harmonic Mean for Average Speed
In addition to the basic formula for distance (), advanced students should be familiar with the Harmonic Mean Formula for calculating average speed when two speeds are given for the same distance. This is particularly useful when an object travels at different speeds for equal distances.
Harmonic Mean Formula for Average Speed
Example Problem: Dr. Steve drove to work at an average speed of 40 miles per hour and returned home at an average speed of 60 miles per hour. What was his average speed for the entire round trip?
Solution:
- Apply the Harmonic Mean Formula:
- Calculate the numerator:
- Calculate the denominator:
- Compute the average speed:
Important Note:
- While your intuition might suggest using the Arithmetic Mean (simple average), the Harmonic Mean is the correct method when calculating average speeds over the same distance traveled at different rates.
- This discrepancy arises because time spent traveling at each speed differs, making the harmonic mean a more accurate representation of overall average speed.
dvanced Math Concepts for the SAT: Triangle Rule and Generalized Pythagorean Theorem
Understanding these advanced concepts can help you tackle higher-level SAT math questions efficiently. Let’s explore each rule with examples.
21. Triangle Inequality Rule
The Triangle Inequality Rule states that the length of any side of a triangle must be greater than the difference of the lengths of the other two sides and less than their sum. Mathematically, for any triangle with sides of length a, b, and c, the following must hold true:
This rule ensures that the sum of any two sides is always greater than the length of the third side.
Example Problem: If is an integer, how many different triangles can be formed with sides of lengths 2, 6, and ?
Solution:
- According to the Triangle Inequality Rule: Simplifying this:
- Since must be an integer, possible values for are 5, 6, and 7.
Answer: There are three possible triangles.
22. Generalized Pythagorean Theorem
The Generalized Pythagorean Theorem is used to find the length of the diagonal (d) in a rectangular solid (a 3D box). For a solid with length a, width b, and height c, the formula is:
d2=a2+b2+c2
Example Problem: A rectangular box has dimensions of length 3 feet, width 4 feet, and height 12 feet. What is the longest distance from one corner of the box to the opposite corner (the length of the diagonal)?
Solution:
- Use the formula: d2=32+42+122
- Calculate each term: d2=9+16+144=169
- Find the length of the diagonal: d=169=13 feet
Answer: The longest distance from one corner of the box to the opposite corner is 13 feet.
Understanding Quadratic Functions and the Vertex Formula
Quadratic functions are fundamental in algebra and are commonly tested on the SAT. Here’s what you need to know about their general form, vertex calculation, and behavior:
General Form of a Quadratic Function
The general form of a quadratic function is:
- The graph of this function is a parabola.
- Vertex Formula: The -coordinate of the vertex of the parabola is given by:
- The direction in which the parabola opens depends on the sign of a:
- Upward if
- Downward if
Example Problem
Given the function , find the value of at which the function has its maximum value.
Solution:
Identify coefficients:
Calculate the x-coordinate of the vertex using the formula:
Substitute the values of a and b:
Explanation:
- Since , the parabola opens downward, indicating that the vertex represents the maximum value of the function.
Answer: The function has its maximum value at .
Key Takeaways:
- The vertex formula allows you to find the vertex of any parabola in the form .
- The sign of a determines the direction of the parabola (upward or downward).
- Understanding how to find the vertex helps determine maximum or minimum values of the quadratic function.
The Standard Form of a Quadratic Function
The standard form of a quadratic function is given by:
- The graph of this function is a parabola.
- The vertex of the parabola is at the point .
- The direction in which the parabola opens depends on the sign of a:
- Upward if
- Downward if
Example Problem
Given the function , for what value of will the function have its minimum value?
Solution:
Identify the parameters:
Determine the vertex:
- The vertex is at .
Interpret the graph:
- Since , the parabola opens upward, indicating that the vertex represents the minimum value of the function.
Answer: The function has its minimum value when .
Remark: Note that in this example 𝑘 = 2, and it is on the right hand side of the equation instead of on the left.
Total Interior Degrees of an n-Sided Polygon
The total number of degrees in the interior of an -sided polygon is given by the formula:
This formula works for any polygon with sides.
Example Problem
Calculate the total interior degrees of an eight-sided polygon (octagon):
- Apply the formula:
- Calculate:
Each Angle of a Regular Octagon:
- In a regular polygon, all sides and angles are equal.
- To find the measure of each interior angle of a regular octagon:
Remark:
A regular polygon is defined as a polygon with all sides equal in length and all angles equal in measure.
Area of an Equilateral Triangle
In advanced geometry problems, you may encounter the need to find the area of an equilateral triangle. An equilateral triangle has all sides of equal length, and its angles are each . While one approach involves splitting the triangle into two 30-60-90 right triangles, a quicker method is to use the following formula:
Formula for the Area of an Equilateral Triangle:
where s is the length of a side of the triangle.
Example Problem
Find the area of an equilateral triangle with a side length of 2 inches.
Solution:
- Apply the formula:
- Substitute the given value:
- Calculate:
-
Answer: The area of the equilateral triangle is square inches.
Counting the Number of Consecutive Integers
To find the number of consecutive integers from a to , inclusive, use the following formula:
Formula:
Remark:
- The word “inclusive” means that both endpoints and are included in the count.
Example 1:
Find the number of integers from 2 to 7.
Solution:
Verification: The integers in the list are 2, 3, 4, 5, 6, and 7, confirming that there are 6 integers.
Example 2:
Find the number of integers from 62 to 512.
Solution:
Point-Slope Form of the Equation of a Line
The point-slope form of an equation of a line is given by:
- Here, is the slope of the line.
- is a point on the line.
Example Problem
Write an equation of the line that has a slope of 2 and passes through the point .
Solution:
Given values:
- (slope)
Substitute the values into the point-slope formula:
Simplifying:
Result: The equation of the line is:
Point-Slope Form of the Equation of a Line
The point-slope form of the equation of a line is:
- m represents the slope of the line.
- is a point on the line.
Example Problem
Write an equation for the line with a slope of 2 that passes through the point .
Solution:
Given values:
- Slope (m) = 2
- Point ( ) =
Substitute the values into the point-slope form:
Simplify:
Result: The equation of the line is:
This form is particularly useful for finding the equation of a line when you know a point on the line and its slope. It can be easily transformed into other forms, such as the slope-intercept form , by further simplifying. This is an essential tool in coordinate geometry and helps solve many line-related problems efficiently.
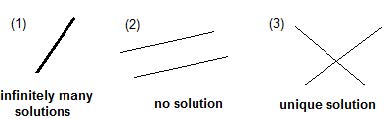
Comparing Lines Through Equations
Identifying Lines That Represent the Same Line
Consider the two equations:
- To check if these equations represent the same line, observe their ratios:
- Alternatively, let . When multiplying:
This confirms that both equations represent the same line.
Identifying Parallel but Distinct Lines
Consider the following equations:
- In this case:
- Since the ratios of the coefficients of and are equal but the ratio of the constants is not, these lines are parallel but distinct.
Identifying Intersecting Lines
Consider these equations:
- Here:
- Since the ratios of the coefficients of and are not equal, these lines are intersecting.
Converting Between Degree Measure and Radian Measure
To convert between degrees and radians, use the following ratio:
Example:
- Convert 90 degrees to radians:
- Convert 3π radians to degrees:
Summary:
- To determine whether two linear equations represent the same line, parallel lines, or intersecting lines, compare the ratios of their coefficients.
- The conversion between degrees and radians can be achieved using the ratio .
This approach helps in analyzing the relationships between lines and converting angles, both of which are important skills for geometry and trigonometry problems on standardized tests like the SAT.
Converting Degrees to Radians
To convert an angle from degrees to radians, use the following formula:
Example 1: Convert 45° to Radians
Solution:
- Apply the conversion formula:
- Simplify the fraction:
- Reduce the fraction:
Shortcut: To convert degrees to radians quickly, multiply the given angle by .
Summary:
- 45° is equivalent to radians.
- The conversion from degrees to radians is straightforward using the factor , which makes it easy to switch between the two units of angle measurement.
Basic Transformations of the Graph of a Function
Vertical Shifts:
- Upward Shift: The graph shifts up by units.
- Downward Shift: The graph shifts down by units.
Horizontal Shifts:
- Rightward Shift: The graph shifts right by k units.
- Leftward Shift: The graph shifts left by units.
Reflections:
- Reflection in the -axis: The graph is reflected over the -axis, effectively flipping it vertically.
- Reflection in the -axis: The graph is reflected over the -axis, effectively flipping it horizontally.
Applying Transformations to the Function
Given the basic transformations:
- Shift Right by 3 Units: To shift the graph of right by 3 units, replace with :
- Shift Down by 2 Units: To shift the graph down by 2 units, subtract 2 from the function:
Resulting Function:
The new function after applying these transformations is: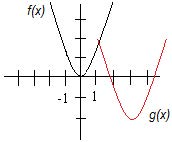
Square Root Property
The square root property states that if:
then:
Example: Consider the equation:
Applying the square root property:
So, the solutions are:
Quadratic Formula
For any quadratic equation of the form:
the solutions for x can be found using the quadratic formula:
Example Problem
Solve the equation:
Step-by-Step Solution:
Identify coefficients:
Apply the quadratic formula:
Simplifying:
Calculate the solutions:
- First solution:
- Second solution:
Result: The solutions are:
Since we want the positive solution for x, the answer is:
Standard Form of the Equation of a Circle
The standard form for the equation of a circle is given by:
- represents the center of the circle.
- r represents the radius of the circle.
Example Problem
Given the circle’s equation:
Find the center and radius:
Identify the values of h and k:
- means .
- can be rewritten as , so .
Therefore, the center of the circle is:
Identify the value of r:
- The equation is in the form .
- Here, , so the radius is:
Result:
- Center:
- Radius:
Remark:
- Note that in the term , it is equivalent to , indicating that the value of is , not .
Given Equation:
Step 1: Completing the Square for the Terms
- Group the terms:
- Complete the square:
- Take half of the coefficient of (which is −8), square it, and add/subtract it:
- Add and subtract 16:
Step 2: Completing the Square for the y Terms
- Group the terms:
- Complete the square:
- Take half of the coefficient of (which is ), square it, and add/subtract it:
- Add and subtract 25:
Step 3: Substitute Back into the Original Equation
Replace the completed squares into the original equation:
Combine like terms:
Add 26 to both sides:
Result:
- The equation is now in the standard form , where the center is .
- Center:
- Radius: (not needed for the problem but derived from the equation).
Answer: The center of the circle is .
1. Factor Theorem
The factor theorem states:
- A number r is a root of the polynomial if and only if is a factor of .
Example:
Given the polynomial:
Since:
it means that is a factor of .
2. Remainder Theorem
The remainder theorem states:
For a polynomial , if it is divided by , the remainder is equal to .
Note: The factor theorem is a specific case of the remainder theorem where the remainder is .
Example:
Consider:
Since:
it means the remainder when divided by is .
3. General Exponential Functions
An exponential function is generally represented as:
- : Initial amount ( )
- : Growth or decay rate ( indicates growth, indicates decay)
Examples:
Population Growth:
- Function:
- This describes a population growing at a 100% growth rate per year, starting with 300 units. The population doubles each year.
Growth with Different Rate:
- Function:
- This represents a population with a 200% growth rate every 6 months, starting at 50. The tripling occurs every 6 months due to .
Exponential Decay:
- Function:
- Models a substance decaying at 25% every 3 years, starting at 120 grams. The decay occurs every 3 years since .
Doubling Over Time:
- Function:
- This models a quantity doubling every years, starting with at .
Key Points Recap:
- Factor Theorem helps identify roots and factors of polynomials.
- Remainder Theorem allows for determining remainders when dividing polynomials.
- Exponential Functions are useful for modeling growth and decay over time, using initial values and rates to describe the changes.







