Mastering Acid-Base Titrations: A Comprehensive Guide
Acid-base titrations may sound intimidating, but they bring together all the key concepts of equilibrium, pH, pKa values, and stoichiometry in a single, fascinating procedure. In this guide, we’ll explore what acid-base titrations are, how they work, and how to tackle various types of titrations with confidence. By the end, you’ll have a clear understanding of titration curves, the equivalence point, and how to work with weak and strong acids and bases in titration problems.
What is a Titration?
A titration is a laboratory technique used to determine the concentration of an unknown solution, or “analyte,” by reacting it with a solution of known concentration, or “titrant.” The titrant is added from a burette until the equivalence point is reached, where the moles of the analyte equal the moles of the titrant.
Equation for the Equivalence Point:
where
n and
m are the stoichiometric coefficients, and
M and
V are the molarity and volume of the solutions.
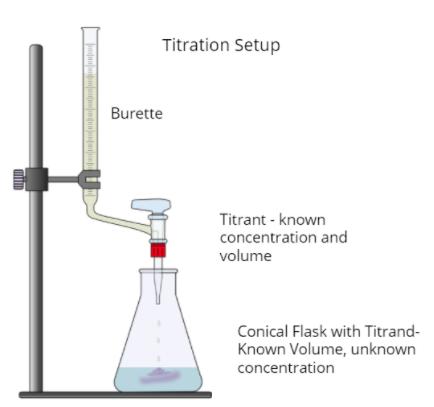
Image from Pixabay
Understanding Titration Curves
During a titration, we measure how the pH changes as we add the titrant. This gives us a titration curve, which shows how pH varies with the volume of titrant added.
Example: Titrating 1M NaOH into 25 mL of 1M HCl
Pre-Titration:
- Initial pH of 1M HCl = 0 (since pH =
−log[1]).
- Initial pH of 1M HCl = 0 (since pH =
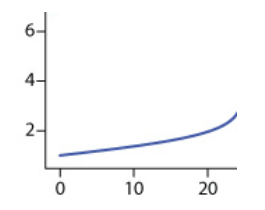
Pre-Equivalence Point:
- As NaOH is added, it reacts with HCl:
- As long as there is excess H+, the pH will gradually rise.

Image From ASDL
- As NaOH is added, it reacts with HCl:
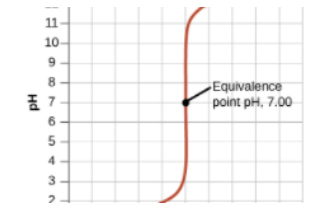
Equivalence Point:
- At this point, the moles of HCl and NaOH are equal. For this example:
- 25 mmol of HCl = 25 mmol of NaOH.
- The pH at the equivalence point is 7 for strong acid-strong base titrations.

Image From LibreTexts/14%3A_Acid-Base_Equilibria/14.07%3A_Acid-Base_Titrations)
- At this point, the moles of HCl and NaOH are equal. For this example:
Post-Equivalence Point:
- Adding more NaOH results in excess OH-, raising the pH.

Image From LibreTexts/14%3A_Acid-Base_Equilibria/14.07%3A_Acid-Base_Titrations)/14%3A_Acid-Base_Equilibria/14.07%3A_Acid-Base_Titrations)/14%3A_Acid-Base_Equilibria/14.07%3A_Acid-Base_Titrations)
- Adding more NaOH results in excess OH-, raising the pH.
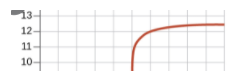
Titration Curve Visualization
A typical titration curve for a strong acid and a strong base shows a steep increase in pH at the equivalence point.

Image From LibreTexts/21%3A_Acids_and_Bases/21.19%3A_Titration_Curves)
Weak Acid-Strong Base Titrations
When a weak acid is titrated with a strong base, the process is similar but with important differences:
- Before the equivalence point, the solution contains a buffer (a mixture of the weak acid and its conjugate base).
- The pH at the half-equivalence point (when half of the acid has reacted) equals the pKa of the acid.
- The pH at the equivalence point is greater than 7 due to the presence of the conjugate base.
Example Problem: Calculate the pH when 10 mL of 0.1M NaOH is added to 25 mL of 0.1M acetic acid (CH₃COOH).
Reaction Equation:
Calculate Millimoles:
- Acetic acid:
- NaOH:
- Acetic acid:
Stoichiometry:
- Remaining CH₃COOH:
- Produced CH₃COO-:
mmol.
- Remaining CH₃COOH:
Calculate pH using the Henderson-Hasselbalch Equation:
Titrations with Weak Bases and Strong Acids
The process for a weak base-strong acid titration follows the same principles, but the pH at the equivalence point will be acidic due to the presence of the conjugate acid.
Quick Tips for Titrations
- Identify the type of titration (strong vs. weak acids/bases).
- Calculate millimoles and use stoichiometry.
- Recognize buffer regions and half-equivalence points.
- Use the Henderson-Hasselbalch equation for buffer solutions.
- Know that pH at the equivalence point varies based on the acid/base strength.
Key Takeaways
- Titrations help determine unknown concentrations by neutralizing an acid or base.
- Titration curves graph pH changes, revealing key points like equivalence.
- Weak acids/bases create buffers during titrations, resulting in unique curves and pH values.
- Mastering stoichiometry, pH calculations, and buffer concepts is essential for tackling titration problems.