6.5 Energy of Phase Changes
Understanding Energy in Phase Changes
Phase changes involve the transformation of a substance from one state of matter to another—solid to liquid, liquid to gas, and vice versa. These transformations can either absorb or release energy, making them either endothermic or exothermic processes. To visualize these changes and better understand the energy required or released, heating curves, cooling curves, and phase diagrams serve as essential tools.
Heating Curves and Energy Absorption
A heating curve illustrates how temperature changes as heat is added to a substance, causing it to transition through different states (solid → liquid → gas). Here’s a breakdown of what happens:

Image Courtesy of Schoenherr & Diamantopoulos Chemistry Videos
- X-axis: Represents the time or progression of heat addition.
- Y-axis: Represents the temperature.
Plateaus on the Heating Curve
The plateaus in a heating curve mark where energy is used for phase changes instead of increasing temperature:
- Melting Point: Energy is absorbed to convert a solid to a liquid (heat of fusion, Hf).
- Boiling Point: Energy is absorbed to convert a liquid to a gas (heat of vaporization, Hv).
Key Insight: The heat of vaporization is generally higher than the heat of fusion because breaking all intermolecular forces to form a gas requires significantly more energy.
Example Calculation: Heating Water from Ice to Steam
Problem: Calculate the energy required to change 30.0 g of ice at -20°C to steam at 140°C.
Given Data:
- Specific heat of ice = 2.108 J/g°C
- Specific heat of water = 4.18 J/g°C
- Specific heat of steam = 2.010 J/g°C
- Hf for H₂O = 334 J/g
- Hv for H₂O = 2260 J/g
Solution Steps:
- Heat the ice (solid):
- Melt the ice (fusion):
- Heat the water (liquid):
- Vaporize the water:
- Heat the steam (gas):
Total Energy Required:
Cooling Curves and Energy Release
A cooling curve is the reverse of a heating curve and represents exothermic processes where energy is released:
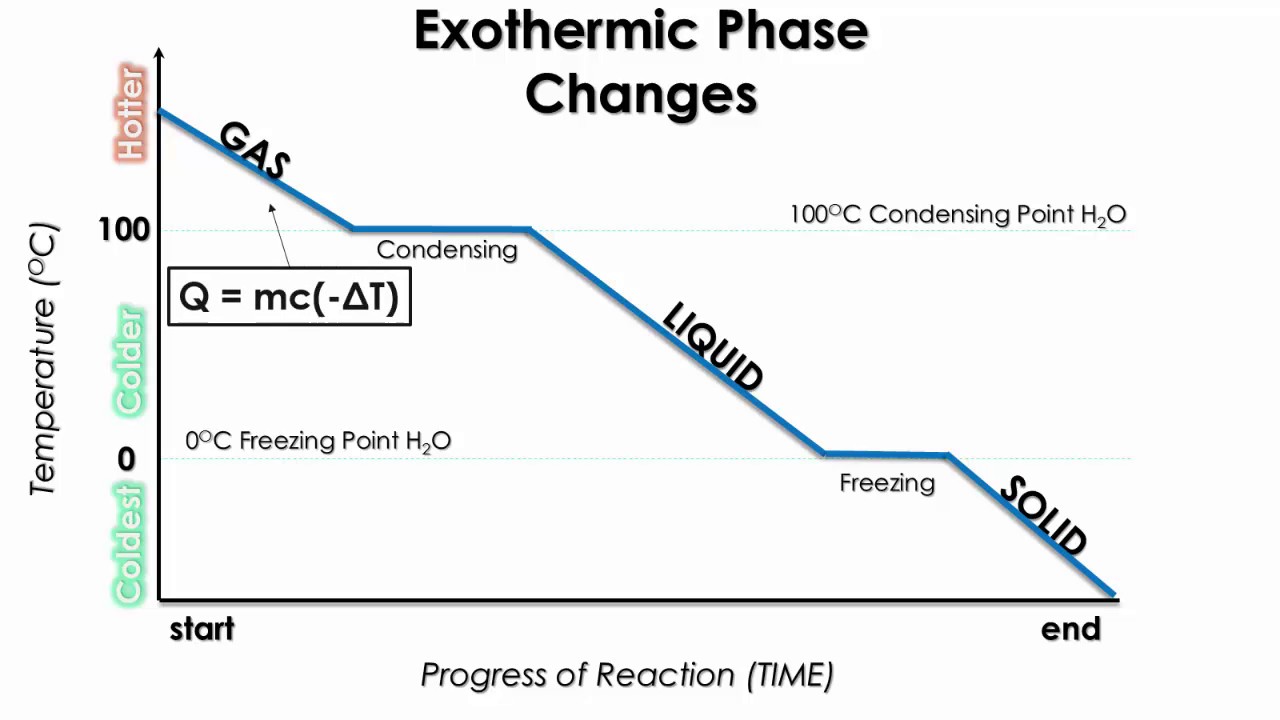
Image Courtesy of Schoenherr & Diamantopoulos Chemistry Videos
- Heats of Condensation and Freezing are the negatives of the heats of vaporization and fusion, respectively.
Tip: Pay close attention to units when calculating energy changes (e.g., J/g, J/mol). Convert as necessary to ensure consistency.
Phase Diagrams: Pressure, Temperature, and States of Matter
Phase diagrams depict the relationship between pressure, temperature, and the state of matter of a substance.
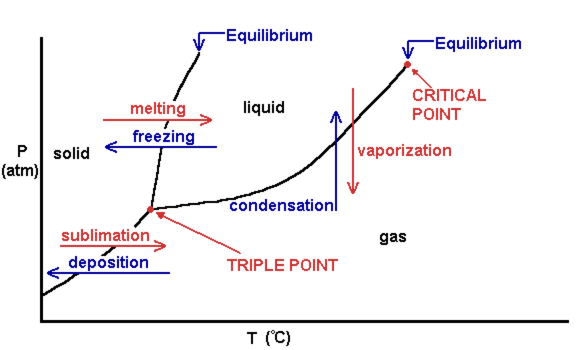
Image Courtesy of Aakash Shah
- Triple Point: The temperature and pressure at which all three states coexist.
- Critical Point: Beyond this point, a liquid cannot exist, and the substance becomes a supercritical fluid.
Example Animation: Watch water reach its triple point, transitioning between solid, liquid, and gas simultaneously!

Image Courtesy of UCSC Physics
Practice FRQ: Energy in Combustion and Phase Changes
Problem (from 1995 AP Exam):
Propane (C₃H₈) is used as fuel for cooking.
(a) Write the balanced equation for the combustion of propane.
(b) Calculate the volume of air needed to burn 10.0 g of propane (assuming air is 21% O₂ by volume).
(c) Given the heat of combustion of propane is -2,220.1 kJ/mol, calculate the heat of formation (ΔHf) of propane.
(d) If 30.0 g of propane is burned and all heat is transferred to 8.00 kg of water (specific heat = 4.18 J/g°C), find the temperature increase.
Check out the detailed solutions in our practice problems section!
Solution!
(A) 1 point: C3H8 + 5 O2 –> 3 CO2 + 4 H2O
(*phases do not need to be listed for full point to be given)
(**if the equation is balanced wrong, no credit is given for part (A) but credit can still be earned if part (B) + (C) are consistent with the incorrectly balanced equation — use this fact to your advantage on the AP exam and write down any answer even if you are not totally sure while working)
(B) 4 points:
(answer must be consistent with part (A) to receive credit; each line is worth 1 point)

(C) 2 points:

(D) 2 points:
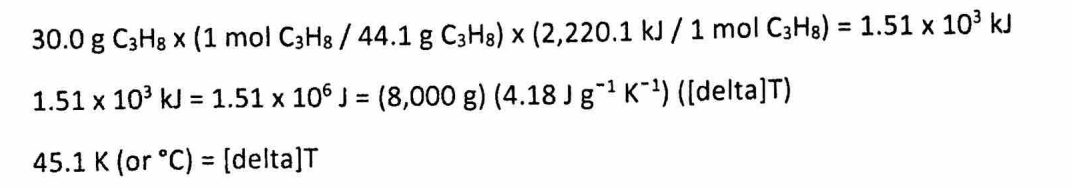
Final Thoughts
Understanding energy in phase changes is crucial for predicting and analyzing how substances behave during temperature and state changes. By mastering heating and cooling curves, as well as phase diagrams, you’ll be well-prepared for complex calculations and real-world applications!