Understanding Rate Laws in Chemistry Kinetics
What is a Rate Law?
When studying chemical kinetics, we know that increasing the concentration of a reactant often increases the reaction rate. But how much faster does the reaction proceed with a concentration increase? The answer lies in the rate law.
A rate law describes the relationship between the rate of a chemical reaction and the concentrations of its reactants. It is expressed by the formula:
R=k[A]n[B]m…
where:
- R is the reaction rate.
- k is the rate constant.
- [A] and [B] are the concentrations of reactants A and B.
- n and m represent the reaction orders for each reactant.
The reaction orders, n and m, are experimentally determined values that reveal how changes in the concentration of each reactant affect the reaction rate. Note that this equation can have more than two reactants, but for most AP Chemistry problems, you’ll encounter no more than two.
Animation Courtesy of GIPHY; We’ll delve deeper into collisions later in this unit.
Understanding Reaction Order
Reaction order indicates how the reaction rate responds to changes in the concentration of a reactant. For instance, if we have a rate law:
R=k[A]2[B]1
This tells us that:
- Doubling [A] will quadruple the reaction rate (since 2² = 4).
- Doubling [B] will double the reaction rate.
The overall reaction order is the sum of the orders of each reactant. For our example, the overall order is 3 (2 for A + 1 for B).
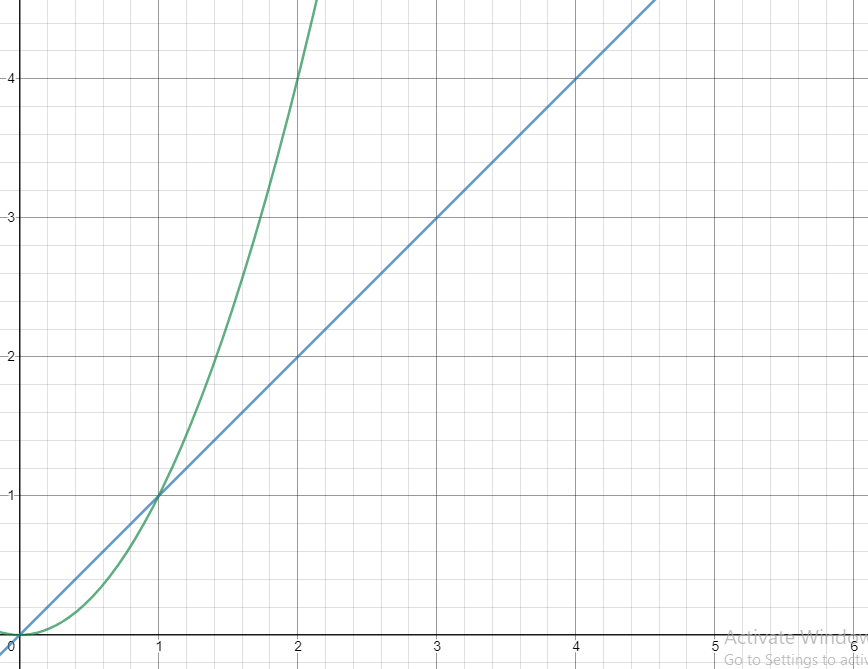
Quadratic vs. Linear Relationships (x^2 vs x)
Determining Reaction Order Experimentally
Rate laws cannot be deduced from the balanced chemical equation alone; they must be determined experimentally. Chemists run several trials, adjusting reactant concentrations, to observe how changes affect the reaction rate.
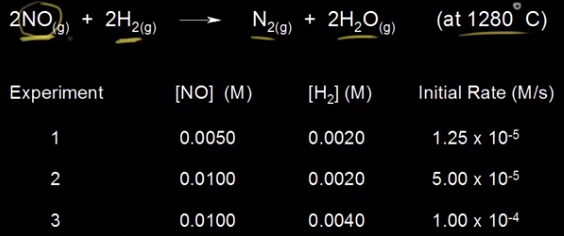
Example:
Consider the reaction:
2NO+2H2→N2+2H2O
Experimental data is provided for three trials, each with varying reactant concentrations and observed rates.
Compare Trials 1 and 2:
- [NO] doubles, while [H₂] remains constant.
- The rate quadruples (from 1.25 × 10⁻⁵ to 5.00 × 10⁻⁵ M/s).
- Therefore, the reaction is second-order with respect to NO.
Compare Trials 2 and 3:
- [H₂] doubles, while [NO] remains constant.
- The rate doubles (from 5.00 × 10⁻⁵ to 1.00 × 10⁻⁴ M/s).
- Therefore, the reaction is first-order with respect to H₂.
Resulting Rate Law:
R=k[NO]2[H2]1
The rate constant, k, can be determined by substituting data from any trial into the rate law. For example, using data from trial 1:
k=[NO]2[H2]R=250M−2s−1
What is the Rate Constant (k)?
The rate constant (k) serves as a proportionality constant that quantifies how quickly a reaction occurs. Key characteristics of k:
- Temperature Specific: The value of k changes with temperature.
- Units Depend on Reaction Order: The units of k change based on the overall reaction order.
Units of k Based on Reaction Order
- Zeroth Order: R=k[A]0
- Simplifies to R=k.
- Units: M/s.
- First Order: R=k[A]1
- Units: s⁻¹.
- Second Order: R=k[A]2
- Units: M⁻¹s⁻¹.
Practical Examples and Applications
- Reaction with Order 2: Doubling a reactant’s concentration increases the reaction rate by a factor of 4.
- Reaction with Order 1: Doubling a reactant’s concentration doubles the reaction rate.
Rate laws are essential for predicting how changes in concentration affect reaction rates, making them crucial in fields like chemical engineering, pharmaceuticals, and environmental science.







