4.2 Current-Carrying Wires & Magnetic Fields

4.2 Current-Carrying Wires & Magnetic Fields

Comprehensive Guide

Magnetic fields generated by current-carrying wires are essential to understanding electromagnetism and its applications. In this guide, we delve into the interactions between wires and magnetic fields, explore forces between wires, and explain key concepts like torque and magnetic field strength. By mastering these topics, you’ll gain a deeper understanding of phenomena fundamental to technologies such as electric motors and magnetic sensors.

Forces on a Wire in an External Magnetic Field

When a current-carrying wire is placed in a magnetic field, it experiences a force. This force is described by the equation:

Where:

• : Force on the wire (N)

• : Current in the wire (A)

• : Length of the wire in the magnetic field (m)

• : Magnetic field strength (T)

• : Angle between the current direction and the magnetic field.

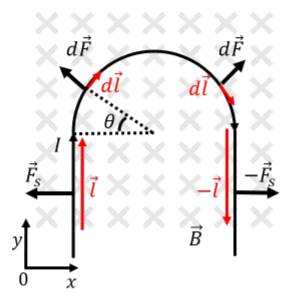
Right-Hand Rule for Current-Carrying Wires

To determine the direction of the force:

1. Point your thumb in the direction of the current.

2. Point your fingers in the direction of the magnetic field.

3. Your palm indicates the direction of the force.

Example:

• A straight wire carrying a current is placed in a uniform magnetic field directed into the page.

• The force on the wire can be calculated using if , simplifying the equation.

For curved sections of the wire, symmetry can simplify calculations. For example, in a semicircular loop, the horizontal forces cancel, leaving only vertical components to consider.

Torque on a Wire Loop in a Magnetic Field

Even though a closed loop of wire in a magnetic field experiences no net force, it can still experience torque. This principle underlies the operation of electric motors.

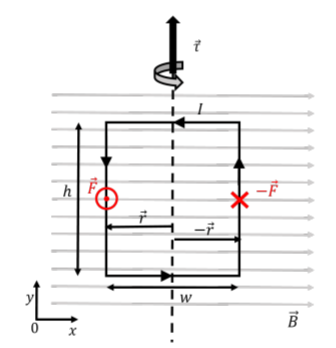
Example: Rectangular Loop

Consider a rectangular loop of wire carrying current placed in a uniform magnetic field:

• The magnetic force acts on opposite sides of the loop, creating a torque.

• Torque is given by:

Where:

• : Number of turns in the loop

• : Area of the loop

• : Angle between the magnetic field and the normal to the loop.

As the loop rotates, it reaches an equilibrium position where the torque becomes zero. This cyclic rotation is harnessed in electric motors to convert electrical energy into mechanical energy.

Magnetic Fields from Current-Carrying Wires

A current-carrying wire generates a magnetic field, forming concentric circles around the wire. The strength of this field is given by:

Where:

• : Magnetic field strength (T)

• : Permeability of free space ( N/A)

• : Current in the wire (A)

• : Distance from the wire (m)

Right-Hand Curl Rule (RHCR)

To determine the direction of the magnetic field:

1. Point your thumb in the direction of the current.

2. Curl your fingers around the wire.

3. Your fingers point in the direction of the magnetic field.

Example:

• A wire carrying current upward generates a magnetic field that circles clockwise when viewed from above.

Forces Between Parallel Wires

Two parallel current-carrying wires exert forces on each other due to their magnetic fields. The force per unit length between two wires is:

Where:

• : Force per unit length (N/m)

• : Currents in the wires (A)

• : Distance between the wires (m)

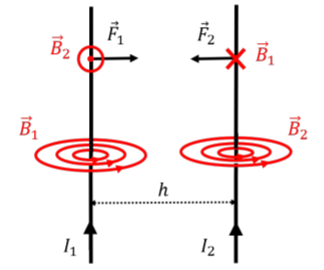
Attraction and Repulsion

• Parallel currents: Attract each other.

• Antiparallel currents: Repel each other.

Example:

• Two wires carrying 5A each, separated by 0.1m, experience an attractive force of:

Drawing Magnetic Fields

Key considerations when visualizing magnetic fields:

• Field Lines: Represent the direction and strength of the magnetic field.

  • Lines closer together indicate stronger fields.

  • Arrows show the direction (north to south outside a magnet).

• Closed Loops: Field lines always form closed loops.

• Current-Carrying Wires:

  • Use RHCR to determine the circular pattern of field lines around the wire.

Practice Problem Examples

Example 1: Current in a Rod

Scenario: A horizontal rod with current flows in a magnetic field . The rod is suspended by wires and located above a long conducting cable.

1. Current Direction in the Rod:

   • Conventional current flows counterclockwise, so the current in the rod flows to the left.

2. Current Direction in the Cable:

   • To lift the rod, the magnetic field created by the cable must oppose the rod’s magnetic field. The current in the cable must flow to the right.

3. Minimum Cable Current:

   • To balance gravitational force:

     Using , solve for :

Applications

1. Electric Motors:

   • Convert electrical energy into rotational motion using torque on current loops.

2. Electromagnets:

   • Generate strong, adjustable magnetic fields for industrial and medical applications.

3. Magnetic Sensors:

   • Detect magnetic fields in devices like Hall effect sensors.

Key Takeaways

1. Magnetic Forces:

   • Act on current-carrying wires in external magnetic fields.

   • Depend on current, field strength, and orientation.

2. Field Direction:

   • Use the Right-Hand Curl Rule to determine field directions.

3. Wire Interactions:

   • Parallel currents attract; antiparallel currents repel.