The Collatz Conjecture (or 3n + 1 problem) asserts that iterating a simple process – halve n if n is even, or triple it and add 1 if n is odd – will eventually bring any positive integer to 1. For example, starting from 5 yields the sequence 5 → 16 → 8 → 4 → 2 → 1. No matter which number you start with, repeated application seems to eventually reach the loop 4 → 2 → 1. Yet despite this simplicity and enormous computational evidence (verified for all numbers up to 2.95×10^20), no general proof is known. The conjecture’s origin traces back to Lothar Collatz in the 1930s, and over time it has acquired many names (Syracuse problem, Ulam conjecture, Kakutani’s problem, etc.). Its allure lies in the contrast between an easy-to-understand definition and an intractable analysis. Leading mathematicians have famously cautioned about its difficulty – Paul Erdős remarked “Mathematics may not be ready for such problems,” and Jeffrey Lagarias noted it is “completely out of reach of present day mathematics”.
Why is Collatz hard? Unlike many problems in number theory, the Collatz iteration is highly non-monotonic and appears chaotic. Traditional proof techniques (e.g. simple induction or finding a monotone invariant) have failed because the sequence can wander up and down in unpredictable ways. Nevertheless, researchers have pursued multiple approaches – from pure number theory and combinatorial reasoning to viewing Collatz as a dynamical system or using heavy computations to gather data. Below we summarize the current state of research, including recent partial breakthroughs, known patterns and results, key obstacles, and notable contributions in tackling this notorious conjecture.
Recent Breakthroughs and Partial Progress
Legitimate progress on Collatz has been scarce, but one breakthrough came in 2019. Terence Tao (Fields Medalist) proved a significant “almost all” result: almost all positive integers eventually reach a value “almost” as small as 1. In precise terms, Tao showed that for any unbounded function f(n) (however slowly it grows), almost every starting number will have some Collatz iterate below f(n). Equivalently, “99% or more” of numbers will eventually dip well below their initial value – e.g. over 99% of numbers up to 1 quadrillion eventually descend below 200 during their trajectory. This landmark result stops short of a full proof (it leaves open a potential exceptional set of zero density), but it is “arguably the strongest result in the conjecture’s history”. Tao’s work introduced techniques from ergodic theory and probability into the problem, treating Collatz orbits like a statistical sampling process rather than trying to deterministically pin down each case. While these methods likely cannot push all the way to a complete proof (the approach loses efficacy as numbers get very small), it demonstrated new ways of thinking about Collatz and showed the conjecture holds for “almost all” numbers in a rigorous sense.
Earlier partial results provided statistical evidence for Collatz. In the 1970s, results by Riho Terras and others proved that the set of starting numbers that eventually go below their initial value has density 1. In other words, almost every Collatz sequence does experience a drop smaller than where it started – a weak but important indication that trajectories tend downward on average. This was strengthened in 1994 by Ivan Korec, who showed almost all orbits dip below n^0.792… of their start. Tao’s 2019 theorem vastly improved these bounds (from a fixed exponent to any slowly growing function). Aside from such density results, no verified proof of the full conjecture exists, although many self-proclaimed “proofs” circulate in recreational mathematics forums. The consensus in the research community is that a qualitative leap in technique would be needed to resolve Collatz, beyond these clever partial successes.
Number Theory Approaches
Most direct attacks on Collatz use tools from number theory, seeking patterns or invariants in the arithmetic of the sequence. Key observations include the following:
- Modular Analysis and Cycles: If a cycle other than the trivial 4→2→1 loop existed, it would satisfy a certain Diophantine equation. Extensive work has shown that any such hypothetical cycle must be astronomically large. In fact, no cycle other than 1-2-4 has been found up to length 186 billion – any nontrivial cycle must contain at least 186 billion numbers. This dramatic lower bound (achieved through modular reasoning and massive search) suggests that small cycles are impossible and pushes any potential counterexample far beyond tested ranges. It bolsters the belief that the only cycle is the trivial 4→2→1 loop.
Bounds on Excursions: Number theorists have studied how large Collatz sequences can grow relative to their starting point. For a sequence to diverge to infinity, it would need to outrun the “downward pull” of the halving steps. Results by researchers like Ilia Krasikov and Jeffrey Lagarias (2003) established inequalities that limit how fast the sequence can climb on average. These difference inequality techniques show, roughly, that exponential growth is incompatible with the Collatz recurrence, except perhaps on a very sparse set of starting values. While such bounds don’t prove convergence, they constrain the behavior of any counterexample.
Parity Sequences: The Collatz process is often studied via the sequence of odd/even steps (parity pattern) it produces. Writing a number in binary, one Collatz step (3n+1 when n is odd) roughly corresponds to a left-shift and add operation. Some research analyzes these parity patterns to detect impossible configurations or invariant properties. For instance, Terras’s theorem essentially considered parity patterns to prove that almost all numbers eventually hit a smaller value. However, no one has found a finite set of “forbidden” parity sequences that would cover all potential counterexamples – the space of sequences is too rich.
Lack of Monotonic Invariant: A major hurdle is that there’s no known arithmetic function of n that consistently decreases (or increases) along Collatz iterations for all n. Many problems in number theory are solved by finding a quantity that always moves in one direction, forcing termination. For Collatz, simple measures like the value of n itself or n mod some base do not work – the value can soar and plummet without obvious regularity. Researchers have tried to define more clever invariants or rank functions, but so far none can handle every case. This is intimately tied to why an inductive proof fails: there isn’t a clear property P(k) that ensures P(k+1) for this nonlinear recurrence.
Nonetheless, number theoretic work has been invaluable in shaving away potential problematic cases. It has yielded the partial results above and provided intuitive justification for why the conjecture should be true (no obvious arithmetic obstructions have been found). Jeffrey Lagarias in 2010 compiled an extensive bibliography and monograph on the 3x+1 problem, documenting these results and strategies. The upshot is that while classical number theory hasn’t cracked Collatz, it has mapped out the landscape of the problem – showing where a counterexample can’t hide (e.g. not at small sizes or in short cycles) and suggesting that any violation of the conjecture would be extraordinarily exotic.
Dynamical Systems Perspective
Another angle is to view the Collatz map as a dynamical system – an iteration of a function – and study its behavior with tools from dynamics and ergodic theory. One fruitful approach is to extend the domain from the natural numbers to the 2-adic integers (a number system useful in number theory). In the 2-adic world, every odd integer has a multiplicative inverse of 2, allowing the Collatz function (including the division by 2) to be defined everywhere continuously. Remarkably, under this extension the Collatz function is measure-preserving and even ergodic with respect to the 2-adic measure. Intuitively, ergodicity means that, in the 2-adic sense, Collatz orbits are “random enough” to eventually explore all sorts of residues. In fact, every possible infinite parity sequence occurs for exactly one 2-adic starting value, and almost all 2-adic initial states produce infinite, aperiodic trajectories. This tells us that, when viewed through the lens of 2-adic dynamics, the Collatz iteration has no hidden cycles or traps for the vast majority of starting points – a result consistent with the conjecture’s claim of eventual descent to 1 in the natural numbers.
The dynamical viewpoint also invites analogies to random walks and other chaotic systems. Tao’s proof, for example, was partly inspired by thinking of Collatz like a stochastic process or a flow in a physical system. By grouping numbers into carefully chosen classes (“weighted” sampling) and tracking how an ensemble of trajectories evolves, he applied a kind of statistical stability analysis akin to those used in studying turbulent fluids or iterative maps. This crossover from dynamical systems provided new insight – treating the Collatz map as almost random but with just enough structure to analyze in aggregate.
Researchers have even experimented with extending Collatz to the real or complex numbers (defining a piecewise-linear or analytic function that agrees with 3x+1 on the integers) to visualize its behavior. Cobweb plots of orbits in the real extension show a jagged, fractal-like path as the function composes with itself. While such continuous extensions are more curiosities than rigorous tools, they reinforce the notion that Collatz acts like a chaotic dynamical system. The lack of smoothness or monotonicity in these plots mirrors the difficulty of the problem.
In summary, the dynamical perspective underscores why Collatz is so hard: it behaves randomly in many respects. But it also offers hope in the form of ergodic theory and probabilistic methods – as demonstrated by Tao’s work – showing that we can sometimes corral this “chaos” into partial results by averaging techniques. It’s an active angle of research to see if other dynamical or algebraic structures (perhaps an as-yet-undiscovered symmetry or conserved quantity in the Collatz map) could lead to a breakthrough.
Computer-Assisted Analysis
Given the difficulty of a theoretical proof, a lot of effort has gone into computational verification and exploration of the Collatz conjecture. This has produced impressive results and some of the “known bounds” cited earlier:
Enormous Verification Range: As of recent years, computers have verified the Collatz conjecture for all starting numbers up to $2^{68} \approx 2.95\times 10^{20}$. This exhaustive search (performed by collaborative projects and optimized algorithms) found no counterexample – every tested number eventually reaches 1. The range continues to be extended; for instance, a 2019–2020 project checked all numbers below $2^{68}$ (~300 quintillion) using distributed computing. Such computations provide empirical certainty for finite ranges, though of course they can never fully prove an infinite conjecture. They do, however, greatly raise the bar for any potential counterexample or cycle.
Optimized Algorithms: Verifying Collatz up to such huge limits required clever algorithms. Researchers developed ways to avoid redundant work by analyzing the Collatz graph (the directed graph of numbers under the map) and using “acceleration” techniques. One approach compresses the search space by observing that many numbers share common trajectories after a point (tree-like structures converge). A recent paper by David Barina (2020) introduced a method to replace huge look-up tables with on-the-fly calculations, enabling checking billions of 128-bit numbers per second on modern hardware. Thanks to such innovations, the computational frontier keeps advancing, giving more confidence in the conjecture’s truth.
Search for Cycles: Computer searches have also been used to look for non-trivial cycles or diverging orbits. So far, none have been found within astronomically large bounds. As mentioned, any cycle would have to be incredibly long – and any diverging trajectory (one that tends to infinity) would have to evade detection up through $10^{20}$, which seems increasingly unlikely. Additionally, researchers showed that if a divergent trajectory exists, it would cause certain residues to appear with anomalously high frequency, something not observed in computation. These negative results (no cycles, no divergence seen) align with theoretical expectations that such phenomena are improbable.
Data and Patterns: The massive computations also produce data that can be analyzed statistically. For example, we can record the “total stopping time” (number of steps to reach 1) for each n, or the peak value reached by each trajectory. This data reveals that some numbers take longer than others in an apparently unpredictable way. The record-holders for stopping time grow slowly as the range increases (e.g. 27 is infamous for taking 111 steps, and there are larger numbers that take even more). The distribution of stopping times for large samples of n seems to roughly follow a bell curve shifted toward relatively small values, with a long tail for rare stubborn cases. All such empirical findings support the conjecture (no clear pattern of failure emerges), but also highlight its complexity – if a counterexample exists, it’s hiding very well among the “random” behavior.
Importantly, computational proof techniques from other domains have also been tried. Some computer scientists frame Collatz as a termination problem in computer code or as a logical formula, then use automated theorem provers or SAT solvers to attempt a proof by exhaustion of cases. These methods have managed to verify the conjecture for various special forms of numbers or to enormous depths, but they ultimately run into the same exponential explosion of cases – essentially shifting the heavy lifting to the computer without intrinsically new insight. So while brute force has dramatically extended our knowledge (and likely would discover a counterexample if one lurked at least up to a certain unimaginably large size), a general proof still seems to require a creative theoretical idea.
Known Patterns, Statistical Results, and Bounds
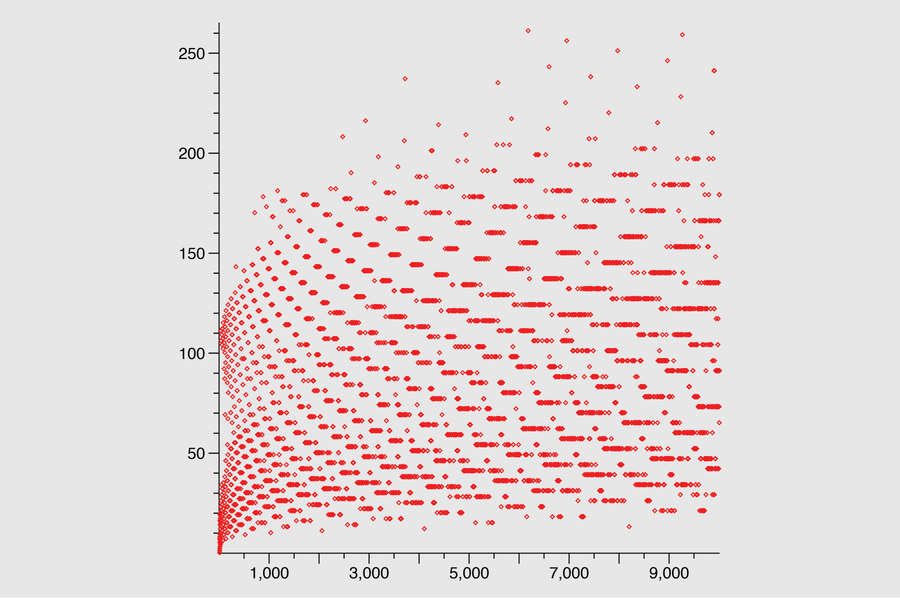
Scatter plot of total stopping times for starting numbers 1 through 9,000 (vertical axis is steps to reach 1). The lengths of Collatz sequences vary greatly and appear random. Some inputs (e.g. 27) produce much longer trajectories than others, but no simple pattern predicts which numbers are “slow”. This unpredictability reflects the conjecture’s complexity.
Despite the randomness, mathematicians have uncovered several patterns and statistical properties of Collatz orbits:
“Hailstone” Behavior: Collatz sequences are often called hailstone sequences because they tend to rise and fall repeatedly (like a hailstone in a cloud) before “falling” to 1. Typically, a sequence will reach a peak value larger than its start, then eventually come down. The number 27, for instance, climbs to 9,232 before descending to 1 after 111 steps. Many numbers show this up-down behavior, and larger starting values generally have larger peaks and longer flight times, though not in a simple linear way.
Shrinking on Average: A classical heuristic by Lagarias (1985) considers the multiplicative effect of steps. An odd step (3n+1) followed by the inevitable even step (÷2) multiplies n by roughly 3/2. Each even step halves n. Statistically, one can model the parity of steps as random: half the time you multiply by ~1.5, and the other half you multiply by 0.5 (for two consecutive evens, multiply by 0.5 twice, etc.). The geometric mean of these factors works out to 3/4, indicating an average shrinkage of about 25% per step. In formula: $(3/2)^{1/2} \times (3/4)^{1/4} \times (3/8)^{1/8} \times \cdots = 3/4$. This suggests that, in a loose sense, Collatz orbits tend downward over the long run, and it would be extremely unlikely for a sequence to buck this trend forever and diverge to infinity.
Stopping Time Distribution: Define the total stopping time $\sigma(n)$ as the number of steps needed for n’s Collatz sequence to reach 1 (excluding the trivial 4-2-1 loop thereafter). Empirically, $\sigma(n)$ is unbounded as n grows – there are always some numbers that take longer than any fixed cutoff. However, the growth is very slow and erratic. Plotting $\sigma(n)$ for n up to large limits produces a scatter (as shown above) with no obvious structure. Some values of n give locally maximal stopping times (these are sometimes called “record highs” or “champions”), but predicting them is difficult. Statistically, most numbers have a relatively small $\sigma(n)$ (on the order of tens or low hundreds), and very large $\sigma$ values are rare. This aligns with Tao’s result that most numbers behave “normally” (their orbits don’t wander too high or too long). The outliers that take a long time are increasingly sparse as the time grows.
Total Stopping Time Bounds: Partial theoretical results give some bounds on $\sigma(n)$. For example, under the assumption that the conjecture is true, $\sigma(n)$ grows slower than $\log n$ for “almost all” n (since Tao’s result implies eventual dips below even extremely slow-growing functions). Unconditionally, it’s known that if $\sigma(n)$ were bounded by a constant, the conjecture would trivially hold – so an open question related to Collatz is whether $\sigma(n)$ is unbounded (most believe it is, as supported by computations). Some heuristic arguments even suggest $\sigma(n)$ might grow about as fast as $\log n$ for random n, but this is far from proven.
No Arithmetic Progressions: One noticeable pattern doesn’t appear: there’s no known arithmetic progression of starting values that all have anomalously large stopping times or any other special behavior. The data doesn’t show any obvious dependence on congruences or other simple number-theoretic classifications – another sign that the Collatz map mixes things “randomly” enough that only density and measure arguments (like Tao’s) seem to get a handle on it.
In summary, the known patterns are mostly statistical. Collatz sequences behave on average one way (drifting downward), but with wild individual variances. This dual nature – predictable in bulk, unpredictable in detail – is a big reason why the conjecture remains unsolved. We can say confidently that a random large number will almost certainly eventually fall to 1 (with probability 1 in a certain sense), but converting that confidence into a deterministically true statement for every specific number is exactly the crux of the problem.
Key Obstacles and Why a Proof is Elusive
Every area of progress above still runs into fundamental obstacles that block a full proof:
Chaotic, Non-Monotonic Trajectories: Collatz iterations don’t consistently move in one direction. A sequence can climb to a huge value before coming down, so one cannot simply show it decreases monotonically to 1. The lack of an ordering or scalar measure that always decreases (or increases) makes well-founded induction difficult. Unlike, say, the Euclidean algorithm for GCD (which decreases the size of numbers each step) or known terminating processes, Collatz defies straightforward “decrease at each step” arguments. Any successful proof must find a more subtle way to guarantee termination.
No Known Invariants: There is no known quantity (modular residue, combination of number theoretic functions, etc.) that remains invariant or follows a simple law under the Collatz mapping for all n. Without an invariant or a conserved property to exploit, one cannot break the problem into simpler subcases easily. Many attempted proofs introduce inventive functions or mappings hoping to find such an invariant, but so far none have worked universally. The problem’s piecewise definition (odd vs even) perhaps inherently thwarts a single neat algebraic invariant.
Extreme Sensitivity to Initial Conditions: Minor changes in the starting number can drastically change the trajectory length and path, reminiscent of a chaotic system. This sensitivity makes it hard to group numbers into manageable classes – each number’s behavior seems unique. Even modern proofs like Tao’s that handle “almost all” cases must carefully control this sensitivity by averaging over many starting values; that approach cannot yet handle the pathological exceptional cases individually.
Probabilistic vs Deterministic Gap: The strongest results (like Tao’s) are probabilistic in nature – they assert what happens for almost every number, or on average. But bridging the gap to a deterministic guarantee (for every number) is huge. An event of probability zero (a possible “rogue” divergent trajectory) is not necessarily impossible logically. Proving it cannot exist at all demands more than probability; it likely requires a delicate counting argument or a new insight into the structure of those exceptional trajectories. This is a leap that current methods haven’t achieved.
Undecidability Concerns: There is a lurking possibility that the Collatz conjecture might be independent of our standard mathematical axioms – meaning it could be impossible to prove or disprove using current accepted methods. This is not just idle speculation: in 1987, John Conway constructed a generalized version of the 3n+1 function that is capable of simulating a universal computer (a Turing machine). In such generalized systems, the question of convergence can encode any computational halting problem, implying those systems are undecidable in general (there is no finite proof for a universal statement about them). While Conway’s result doesn’t directly prove anything about the original Collatz function, it serves as a warning that problems of this flavor can be as hard as the halting problem. It raises the concern that Collatz could, in principle, be independent of Peano arithmetic or ZF set theory – i.e. true but unprovable (or false but unrefutable). Most mathematicians lean toward believing Collatz is true and hopefully provable, but this shadow of undecidability tempers optimism.
Human and Resource Factors: Another “obstacle” often cited informally is the bewitching nature of the problem. Collatz has a reputation for consuming huge amounts of mathematicians’ time for little gain. Its allure and difficulty have caused many researchers to avoid it altogether, fearing a dead-end. As Lagarias quipped, “People become obsessed with it and it really is impossible”. This means the full force of the mathematical community hasn’t been applied to Collatz in the way it was to problems like Fermat’s Last Theorem or the Poincaré Conjecture; many feel it’s just too far ahead of its time. Consequently, collaboration and funding for Collatz-specific research are limited. This sociological factor slows progress – fewer minds tackling the problem means fewer chances of a breakthrough idea.
In summary, the Collatz Conjecture sits at a crossroads of simplicity and complexity – easy to experiment with, yet seemingly immune to the standard arsenal of proof techniques. Any general solution likely requires a novel idea that either tames the chaotic behavior or cleverly sidesteps it. Researchers often joke that solving Collatz might require developing new mathematics that doesn’t yet exist, which is both daunting and exciting.
Notable Mathematicians and Contributions
Many individuals have left their mark on the study of the 3x+1 problem:
Lothar Collatz (1930s): Introduced the $3n+1$ problem during his student years. Though he did not formally publish the conjecture then, his name became attached to it as he promoted it in later years.
Helmut Hasse & Shizuo Kakutani (1950s): Responsible for disseminating the problem to a wider audience. They brought the conjecture to institutions like Syracuse University (hence the name “Syracuse problem”) and helped it gain notoriety.
Stanislaw Ulam: Polish-American mathematician who learned of the problem (possibly from Collatz or colleagues) and discussed it in the 1960s, contributing to its spread in the mathematical community. Some references therefore call it the Ulam conjecture.
Bryan Thwaites: British mathematician who offered an early prize (in the 1980s) for a proof or counterexample, highlighting its reputation as an enticing unsolved puzzle. In some older literature it’s occasionally called “Thwaites’ conjecture.”
Riho Terras (1976): Proved that the set of starting numbers that eventually reach a smaller value than themselves has density 1, providing one of the first rigorous “almost all cases” results. This was a foundational piece of evidence toward believing the conjecture true.
Jeffrey Lagarias: A leading expert on the Collatz problem who compiled an annotated bibliography of everything published on it, and edited The Ultimate Challenge: The 3x+1 Problem (2010). Lagarias himself has contributed multiple papers (often with co-authors like Krasikov, Olenick, etc.) establishing partial results and framing the problem in new ways. He’s also been an advisor warning others of the problem’s difficulty, famously stating it is “extraordinarily difficult – completely out of reach” with current tools.
Paul Erdős: Although Erdős did not directly work on Collatz, he took an interest in it and offered a $500 prize for a solution. His famous quote “Mathematics may not be ready for such problems” encapsulates the sentiment that Collatz might be too advanced for current techniques, coming from one of history’s greatest problem-solvers.
John Horton Conway (1970s–1980s): Studied generalizations of Collatz-like processes. In 1987, he proved that a class of such processes can simulate a Turing machine, implying those general problems are algorithmically undecidable. Conway’s work doesn’t solve Collatz but suggests why it’s a “dangerous” problem – it might inadvertently be as hard as any problem can be.
Terence Tao (2019): Achieved the major partial breakthrough showing almost all Collatz orbits attain almost bounded values. Tao’s work brought powerful analytic tools to bear on the problem and renewed interest in Collatz within the mainstream math community, showing that even “impossible” problems can sometimes yield progress. His result is considered the biggest advance on Collatz in decades.
Others: Numerous mathematicians have contributed insights: Gérard Toulouse and J.C. Lagarias (1970s) on heuristic arguments, Ivan Korec (1994) with improved density results, Ilia Krasikov (early 2000s) with new bounds using difference inequalities, and many unnamed enthusiasts and professionals who tested cases or proposed ideas. While none of these solved the conjecture outright, they each added a piece to the collective understanding. It’s also worth noting the many amateurs and hobbyists who have been drawn to Collatz – a testament to its accessibility – although their proposed proofs have invariably fallen short of the rigorous standards required.
Conclusion
The Collatz Conjecture remains a shining enigma in mathematics: easy enough for anyone to start playing with, yet resistant to the best efforts of experts. The current state of research is a mix of heavy evidence (computational and heuristic) supporting the conjecture, a handful of partial results that cover “almost all” cases or restrict what counterexamples could look like, and a clear understanding of why standard methods fail. We’ve learned a great deal about how Collatz sequences behave – they almost surely go to 1, and they do so with intriguing statistical regularities – but a complete proof demands something fundamentally new. As Alex Kontorovich mused, perhaps we should also keep an open mind to the possibility of a counterexample, however remote, even as the search has turned up nothing.
For now, Collatz stands as an enduring challenge. It has spurred the development of new techniques in ergodic theory and computational testing, and it continues to fascinate both amateurs and professionals. Whether a resolution comes in the form of a brilliant proof or a surprise counterexample (or not at all), studying the problem is enriching mathematics by pushing the boundaries of what we know about simple iterative processes. In the words of Tao, “You can get as close as you want to the Collatz conjecture, but it’s still out of reach.”
The hope is that with fresh insights and perseverance, one day that final gap will be closed and the riddle of 3n+1 will at last be solved – proving once again that even the simplest questions can lead to the deepest mathematics.
Sources: The discussion above is informed by a range of sources, including overviews in Quanta Magazine (quantamagazine.org) and Scientific American (scientificamerican.com), Terence Tao’s 2019 paper arxiv.org, and surveys by Lagarias and others (quantamagazine.org) (en.wikipedia.org). These and other cited references provide further details and context for the current state of the Collatz Conjecture.