Mastering Areas Between Curves and Volumes of Revolution

Calculus allows us to calculate some of the most intricate properties of shapes and spaces, including the area between curves and the volume of revolution. Understanding these concepts can help solve real-world problems in engineering, physics, and beyond. In this blog, we’ll explore these powerful mathematical techniques with easy-to-follow examples.

Finding the Area Between Curves

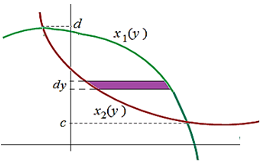
The area between two curves is determined by integrating the difference of the functions over an interval. The general formula for finding the area $A$ between two functions $y = f(x)$ (upper function) and $y = g(x)$  (lower function) over the interval $[a, b]$  is:

$$A = \int_{a}^{b} [f(x) – g(x)] \, dx$$ 

If the curves intersect over multiple intervals, you’ll need to compute the area of each region separately.

Example Problem: Area Between Curves

Let’s find the area between $f(x) = x^2$  and $g(x) = x + 2$  from $x = -1$ to $x = 2$ .

1. Identify the functions:

   • Upper function: $g(x) = x + 2$ 
   • Lower function: $f(x) = x^2$ 

2. Set up the integral:

   $$A = \int_{-1}^{2} [(x + 2) – x^2] \, dx$$ 

3. Evaluate the integral:

   $$A = \int_{-1}^{2} (x + 2 – x^2) \, dx$$ 
   

   Integrating term by term:

   $$A = \left[ \frac{x^2}{2} + 2x – \frac{x^3}{3} \right]_{-1}^{2}$$

   Plugging in the values:

   $$A = \left( \frac{2^2}{2} + 2 \cdot 2 – \frac{2^3}{3} \right) – \left( \frac{(-1)^2}{2} + 2 \cdot (-1) – \frac{(-1)^3}{3} \right)$$ 
   

   Simplifying:

   $$A = \left( 2 + 4 – \frac{8}{3} \right) – \left( 0.5 – 2 + \frac{1}{3} \right) \approx 7.17$$ 

Key Takeaway

Finding the area between curves often involves identifying the upper and lower functions, setting up the integral correctly, and calculating carefully.

Volumes of Revolution

A volume of revolution is created by rotating a region around a given axis. There are two primary methods for calculating such volumes: the disk/washer method and the shell method.

1. Disk/Washer Method

When a region is rotated around the x-axis (or y-axis), we can imagine a series of disks or washers stacked along the axis of rotation. The formula for the volume $V$  using the disk method is:

$$V = \pi \int_{a}^{b} [R(x)]^2 \, dx$$ 

If there’s a hole (washer), subtract the inner radius:

$$V = \pi \int_{a}^{b} \left( [R(x)]^2 – [r(x)]^2 \right) \, dx$$ 

Where:

• $R(x)$  is the outer radius
• $r(x)$  is the inner radius

Example Problem: Volume by Disk Method

Consider the region bounded by $y = \sqrt{x}$ from $x = 0$  to $x = 4$  rotated about the x-axis.

1. Set up the formula:

   $$V = \pi \int_{0}^{4} (\sqrt{x})^2 \, dx = \pi \int_{0}^{4} x \, dx$$ 

2. Evaluate the integral:

   $$V = \pi \left[ \frac{x^2}{2} \right]_{0}^{4} = \pi \left( \frac{4^2}{2} \right) = 8\pi$$ 

2. Shell Method

For the shell method, we imagine cylindrical shells formed by rotating a vertical strip. The formula is given by:

$$V = 2\pi \int_{a}^{b} (radius)(height) \, dx$$ 

Where:

• $radius$ is the distance from the axis of rotation
• $height$ is the function being rotated

Example Problem: Volume by Shell Method

Find the volume of the region bounded by $y = x$ and $y = x^2$  from $x = 0$  to $x = 1$  rotated about the y-axis.

1. Set up the formula:

   $$V = 2\pi \int_{0}^{1} x(x – x^2) \, dx$$ 

2. Evaluate the integral:

   $$V = 2\pi \int_{0}^{1} (x^2 – x^3) \, dx$$ 
   

   Integrating:

   $$V = 2\pi \left[ \frac{x^3}{3} – \frac{x^4}{4} \right]_{0}^{1} = 2\pi \left( \frac{1}{3} – \frac{1}{4} \right) = \frac{\pi}{6}$$

Why It Matters

Areas between curves and volumes of revolution have practical applications in engineering, architecture, and physical sciences. From designing curved surfaces to computing volumes of storage tanks, these calculations help solve real-world challenges.

Closing Thoughts

Mastering these integration techniques opens doors to understanding complex shapes and spaces. With practice, you’ll be able to handle even the most challenging integrals for area and volume. Keep exploring, and don’t hesitate to reach out with any questions or examples you’d like us to cover!

Explore more in-depth mathematical concepts and applications on slyacademy.com. Happy learning!