Traversing 2D Arrays
Traversing 2D Arrays
Traversing 2D Arrays is an essential concept in computer science that builds upon the foundational knowledge of 1D arrays. This topic focuses on effectively accessing, modifying, and performing operations on 2D arrays using nested loops. Let’s delve deeper into this important subject with an emphasis on practical examples and algorithms.
Understanding 2D Arrays
A 2D array is a collection of data organized in rows and columns. You can think of it as a grid or a table. In Java, 2D arrays are arrays of arrays, meaning each element in the outer array is itself an array.
Here’s a quick refresher on our example array arrayB:
int[][] arrayB = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};We’ll use this array throughout this topic.
General Form of Traversing 2D Arrays
Traversing a 2D array requires two nested loops:
The outer loop iterates through rows.
The inner loop iterates through columns.
General Form:
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}This approach ensures you access every element in the 2D array. Depending on the order of loops, you can traverse in row-major or column-major order.
Row-Major vs. Column-Major Traversal
Row-Major Traversal

In row-major traversal, the outer loop iterates through rows, while the inner loop accesses columns.
public static void rowWiseForward(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
System.out.print(array[i][j] + " ");
}
}
}Output for arrayB:
1 2 3 4
5 6 7 8
9 10 11 12 Column-Major Traversal
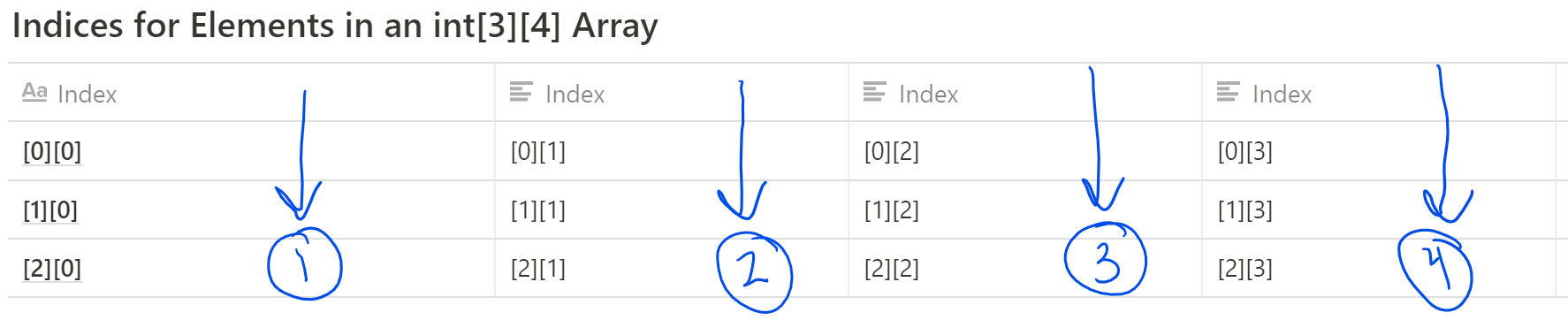
In column-major traversal, the outer loop iterates through columns, while the inner loop accesses rows.
public static void columnWiseForward(int[][] array) {
for (int i = 0; i < array[0].length; i++) {
for (int j = 0; j < array.length; j++) {
System.out.print(array[j][i] + " ");
}
}
}Output for arrayB:
1 5 9
2 6 10
3 7 11
4 8 12 Traversing in Reverse
To traverse rows or columns in reverse order, adjust the loop conditions.
Row-Wise Reverse

for (int i = array.length - 1; i >= 0; i--) {
for (int j = array[i].length - 1; j >= 0; j--) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}Column-Wise Reverse

for (int i = array[0].length - 1; i >= 0; i--) {
for (int j = array.length - 1; j >= 0; j--) {
System.out.print(array[j][i] + " ");
}
System.out.println();
}Advanced Traversal: Snaking Patterns
Example 1: Alternating Row Directions
public static void exampleOne(int[][] array) {
for (int i = 0; i < array.length; i++) {
if (i % 2 == 0) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
} else {
for (int j = array[i].length - 1; j >= 0; j--) {
System.out.print(array[i][j] + " ");
}
}
}
}Output:
1 2 3 4
8 7 6 5
9 10 11 12 Example 2: Alternating Column Directions
public static void exampleTwo(int[][] array) {
for (int i = array[0].length - 1; i >= 0; i--) {
if (i % 2 == 0) {
for (int j = 0; j < array.length; j++) {
System.out.print(array[j][i] + " ");
}
} else {
for (int j = array.length - 1; j >= 0; j--) {
System.out.print(array[j][i] + " ");
}
}
}
}Standard Algorithms with 2D Arrays
Linear Search
public static boolean searchForElement(int[][] array, int element) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
if (array[i][j] == element) {
System.out.println("Found at: Row " + i + ", Column " + j);
return true;
}
}
}
return false;
}Finding Maximum and Minimum
public static int findMax(int[][] array) {
int max = array[0][0];
for (int[] row : array) {
for (int num : row) {
if (num > max) max = num;
}
}
return max;
}
public static int findMin(int[][] array) {
int min = array[0][0];
for (int[] row : array) {
for (int num : row) {
if (num < min) min = num;
}
}
return min;
}Practical Use Cases
Traversing 2D arrays is essential for applications like:
Matrix operations: Addition, subtraction, multiplication.
Game development: Implementing grids for games like Tic-Tac-Toe or Chess.
Data visualization: Creating heatmaps or tabular representations.
Mastering these concepts allows you to perform complex operations on multidimensional data efficiently.
20 Highly Trending FAQs About Traversing 2D Arrays with Detailed Answers
1. What Does Traversing a 2D Array Mean?
Traversing a 2D array involves accessing each element in the array, usually to perform operations like reading, updating, or processing values.
2. How to Traverse a 2D Array in Row-Major Order?
In row-major order, elements are accessed row by row:
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}3. How to Traverse a 2D Array in Column-Major Order?
Column-major traversal accesses elements column by column:
for (int j = 0; j < array[0].length; j++) {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}4. What is the Time Complexity of Traversing a 2D Array?
The time complexity of traversing a 2D array is O(rows × columns), where rows and columns are the dimensions of the array.
5. What Are Real-Life Applications of Traversing 2D Arrays?
Image processing (pixel manipulation).
Navigating game boards.
Matrix operations in mathematics.
Tabular data processing.
6. How to Use Enhanced For Loops for Traversing 2D Arrays?
Enhanced for-loops simplify traversal:
for (int[] row : array) {
for (int value : row) {
System.out.print(value + " ");
}
System.out.println();
}7. How to Access Diagonal Elements in a 2D Array?
Primary diagonal:
for (int i = 0; i < n; i++) {
System.out.print(array[i][i] + " ");
}Secondary diagonal:
for (int i = 0; i < n; i++) {
System.out.print(array[i][n - i - 1] + " ");
}8. How to Traverse Only the Edges of a 2D Array?
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (i == 0 || i == rows - 1 || j == 0 || j == cols - 1) {
System.out.print(array[i][j] + " ");
}
}
}9. What is Spiral Traversal of a 2D Array?
Spiral traversal accesses elements in a circular manner:
int top = 0, bottom = rows - 1, left = 0, right = cols - 1;
while (top <= bottom && left <= right) {
for (int i = left; i <= right; i++) System.out.print(array[top][i] + " ");
top++;
for (int i = top; i <= bottom; i++) System.out.print(array[i][right] + " ");
right--;
if (top <= bottom) {
for (int i = right; i >= left; i--) System.out.print(array[bottom][i] + " ");
bottom--;
}
if (left <= right) {
for (int i = bottom; i >= top; i--) System.out.print(array[i][left] + " ");
left++;
}
}10. How to Traverse a Jagged Array?
Jagged arrays have rows of different lengths:
for (int i = 0; i < jaggedArray.length; i++) {
for (int j = 0; j < jaggedArray[i].length; j++) {
System.out.print(jaggedArray[i][j] + " ");
}
}11. How to Traverse a 2D Array in Reverse Row Order?
for (int i = array.length - 1; i >= 0; i--) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}12. How to Traverse a 2D Array in Zigzag Order?
for (int i = 0; i < array.length; i++) {
if (i % 2 == 0) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
} else {
for (int j = array[i].length - 1; j >= 0; j--) {
System.out.print(array[i][j] + " ");
}
}
}13. What Are the Common Traversal Errors?
Out-of-bounds index.
Skipping elements due to incorrect loop conditions.
Using incorrect dimensions for jagged arrays.
14. How to Traverse Rows with Even Indices Only?
for (int i = 0; i < array.length; i += 2) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}15. How to Calculate the Sum of Elements During Traversal?
int sum = 0;
for (int[] row : array) {
for (int value : row) {
sum += value;
}
}
System.out.println("Sum: " + sum);16. How to Find the Maximum Element During Traversal?
int max = Integer.MIN_VALUE;
for (int[] row : array) {
for (int value : row) {
if (value > max) max = value;
}
}
System.out.println("Max: " + max);17. How to Traverse a 2D Array Using Streams in Java?
Arrays.stream(array).forEach(row -> {
Arrays.stream(row).forEach(value -> System.out.print(value + " "));
System.out.println();
});18. How to Traverse Only Non-Zero Elements in a Sparse Matrix?
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (array[i][j] != 0) {
System.out.print(array[i][j] + " ");
}
}
}19. What is Boundary Traversal of a 2D Array?
Boundary traversal accesses the first and last rows and columns:
for (int i = 0; i < cols; i++) System.out.print(array[0][i] + " ");
for (int i = 1; i < rows; i++) System.out.print(array[i][cols - 1] + " ");
for (int i = cols - 2; i >= 0; i--) System.out.print(array[rows - 1][i] + " ");
for (int i = rows - 2; i > 0; i--) System.out.print(array[i][0] + " ");20. How to Traverse a 2D Array in L-Shaped Order?
for (int i = 0; i < rows; i++) System.out.print(array[i][0] + " ");
for (int j = 1; j < cols; j++) System.out.print(array[rows - 1][j] + " ");






