Heron’s formula

Heron’s Formula – The Timeless Triangle Area Calculator

Introduction to Heron’s Formula

In geometry, Heron’s formula (sometimes referred to as Hero’s formula) is a well-known equation for finding the area of a triangle when the lengths of all three sides are known. The formula is named after Hero of Alexandria, an ancient Greek engineer and mathematician.

Unlike other formulas for calculating the area of a triangle (e.g., half the base times the height), Heron’s formula does not require selecting a base or calculating height separately. This makes it especially useful when only the side lengths are available.

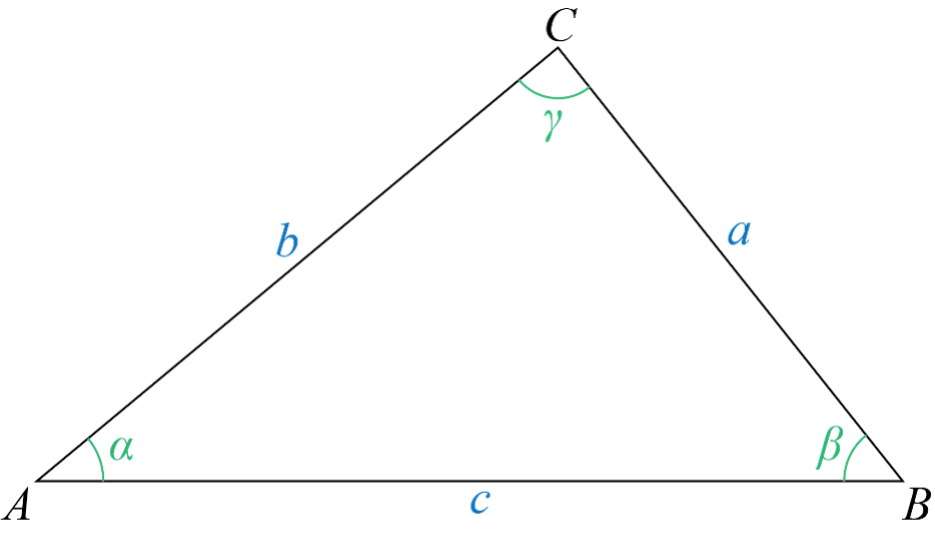
The Formula

Given a triangle with side lengths $a$ , $b$ , and $c$ , the area $A$  is calculated using the following steps:

1. Calculate the semi-perimeter ($s$ ): $$s = \frac{a + b + c}{2}$$
2. Apply Heron’s Formula: $$A = \sqrt{s(s – a)(s – b)(s – c)}$$

Alternate Forms of Heron’s Formula

Heron’s formula can be rewritten in various equivalent forms. Here are a few of them:

1. Using the semi-perimeter expression: $$A = \frac{1}{4} \sqrt{(a + b + c)(-a + b + c)(a – b + c)(a + b – c)}$$
2. An alternate expansion: $$A = \frac{1}{4} \sqrt{2(a^2b^2 + a^2c^2 + b^2c^2) – (a^4 + b^4 + c^4)}$$
3. Another equivalent form: $$A = \frac{1}{4} \sqrt{(a^2 + b^2 + c^2)^2 – 2(a^4 + b^4 + c^4)}$$
4. Expressing it in terms of products of squares: $$A = \frac{1}{4} \sqrt{4a^2b^2 – (a^2 + b^2 – c^2)^2}$$

Why Heron’s Formula Stands Out

What makes Heron’s formula special is that it does not require any arbitrary choice of a side as the base or any knowledge about the triangle’s angles or height. It is derived purely from the side lengths, making it versatile and broadly applicable.

Example Use Cases

1. Example 1: Simple Calculation Consider a triangle with side lengths $a = 7$ , $b = 8$ , and $c = 9$ .

   • Calculate the semi-perimeter: $$s = \frac{7 + 8 + 9}{2} = 12$$ 
   • Calculate the area: $$A = \sqrt{12(12 – 7)(12 – 8)(12 – 9)}$$ $$A = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} \approx 26.83 \text{ square units}$$ 

2. Example 2: Alternate Form Calculation Using an alternate form for a triangle with sides $a = 6$ , $b = 8$ , and $c = 10$ :

   • Calculate the semi-perimeter: $$s = \frac{6 + 8 + 10}{2} = 12$$ 
   • Calculate the area using an alternate form: $$A = \frac{1}{4} \sqrt{(6 + 8 + 10)(-6 + 8 + 10)(6 – 8 + 10)(6 + 8 – 10)}$$ $$A = \frac{1}{4} \sqrt{24 \times 12 \times 8 \times 4} = \sqrt{3840} \approx 24 \text{ square units}$$ 

Historical Context

Hero of Alexandria, who lived around the 1st century AD, was an influential mathematician and engineer. Apart from Heron’s formula, he made significant contributions in the field of mechanics, pneumatics, and geometry. His work on the triangle area formula has stood the test of time, being widely used and admired for its simplicity and elegance.

Applications of Heron’s Formula

• Surveying and Land Measurement: Heron’s formula is commonly used for calculating land area where measurements may only be available in terms of sides.
• Engineering and Architecture: When dealing with triangular sections in design and construction.
• Physics and Astronomy: For calculating areas of triangular projections in various scenarios.

Conclusion

Heron’s formula is a timeless mathematical gem, enabling efficient calculation of triangle areas without the need for height. Its versatility and elegant simplicity make it indispensable in many fields of study and practice. Whether in geometry classes or practical applications, Heron’s formula continues to demonstrate the beauty of mathematics in problem-solving.