Unit 3 Overview: Circular Motion and Gravitation

Seemingly simple actions around us, such as car tires spinning or a satellite orbiting a planet, involve complex physics. In Unit 3 of AP Physics, we delve into these phenomena, building a more intricate understanding of motion and its relationship to gravitational and inertial mass. Misconceptions, like the notion of a centrifugal force, will be addressed, creating clarity around circular motion and gravitation.

This unit makes up 4-6% of the AP exam and typically spans 7-9 forty-five-minute class periods.

Applicable Big Ideas

Big Idea #1: Systems

Objects and systems possess properties like mass and charge, with potential internal structures.

Big Idea #2: Fields

Fields existing in space can explain interactions between objects.

Big Idea #3: Force Interactions

Interactions between objects can be described by forces.

Big Idea #4: Change

Interactions result in changes within and between systems.

Key Concepts

• Vector
• Vector Field
• Uniform Circular Motion
• Centripetal Force
• Gravitational Force
• Newton’s Universal Law of Gravitation
• Gravitational Mass vs. Inertial Mass
• Frame of Reference

Key Equations

• Newton’s Universal Law of Gravitation:

  $$F = G \frac{{m_1 \cdot m_2}}{{r^2}}$$

• Centripetal Acceleration:

  $$a_c = \frac{{v^2}}{r}$$

• Gravitational Field Acceleration:

  $$g = G \frac{M}{R^2}$$

3.1 Vector Fields

Vector fields represent physical quantities with both magnitude and direction. For example, in uniform circular motion, the velocity vector field changes direction but maintains constant magnitude.

Applications:

• Representing velocity, force, acceleration, and magnetic fields.
• Simplified representation for gravitational interactions, e.g., Earth and Moon.

3.2 Fundamental Forces

The four fundamental forces are:

• Gravitational Force: Dominates large-scale phenomena like planetary orbits.
• Electromagnetic Force: Drives interactions between charged particles.
• Weak Force: Responsible for radioactive decay.
• Strong Force: Holds atomic nuclei together.

For AP Physics, the gravitational force is key.

3.3 Gravitational and Electric Forces

The gravitational force equation:

$$F = G \frac{{m_1 \cdot m_2}}{{r^2}}$$

This universal law underpins phenomena from galaxies forming to Earth’s orbit around the Sun.

3.4 Gravitational Field Acceleration

The gravitational acceleration for a planet depends on its mass ($M$) and radius ($R$):

$$g = G \frac{M}{R^2}$$

This equation helps calculate gravitational fields for planets, explaining variations in $g$ across celestial bodies.

3.5 Inertial vs. Gravitational Mass

• Inertial Mass: Resists acceleration.
• Gravitational Mass: Determines interaction with gravity.

Example: A bowling ball and feather fall equally in a vacuum but differently on Earth due to air resistance.

3.6 Centripetal Acceleration and Centripetal Force

Centripetal acceleration keeps objects in circular paths.
Equation:

$$a_c = \frac{{v^2}}{r}$$

Centripetal Force:

$$F = m \cdot a_c = \frac{{m \cdot v^2}}{r}$$

This is the net force directing an object toward the circle’s center.

3.7 Free-Body Diagrams in Circular Motion

Free-body diagrams (FBDs) represent forces in uniform circular motion. Key considerations:

• Align the positive axis with centripetal acceleration (toward the circle’s center).
• Resolve forces into x and y components if necessary.

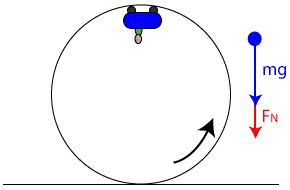
3.8 Applications of Circular Motion and Gravitation

Rotational Analogs:

• Position ($x$) ↔ Angular Position ($\theta$)
• Velocity ($v$) ↔ Angular Velocity ($\omega$)
• Acceleration ($a$) ↔ Angular Acceleration ($\alpha$)

Rotational Kinematics Equations apply when angular acceleration is constant, mirroring linear kinematics.