3.7 Free-Body Diagrams for Objects in Uniform Circular Motion

Free-Body Diagram Basics

A free-body diagram (FBD) is a powerful visual tool used to represent the forces acting on an object. For objects undergoing uniform circular motion, FBDs help analyze motion and understand the forces responsible for keeping an object on its curved path.

How to Draw an FBD

1. Point Mass Representation:

   • Represent the object as a point mass.
   • Draw arrows originating from the dot to show forces acting on the object.

2. Force Points of Application:

   • Consider where the forces are applied. For example, friction acts at the contact point, while gravitational force acts at the object’s center of mass.

Coordinate System

In uniform circular motion, the positive axis (x or y) should align with the centripetal force, which always points toward the center of the circle. Forces not aligned with this axis should be broken into their components.

FBDs for Uniform Circular Motion

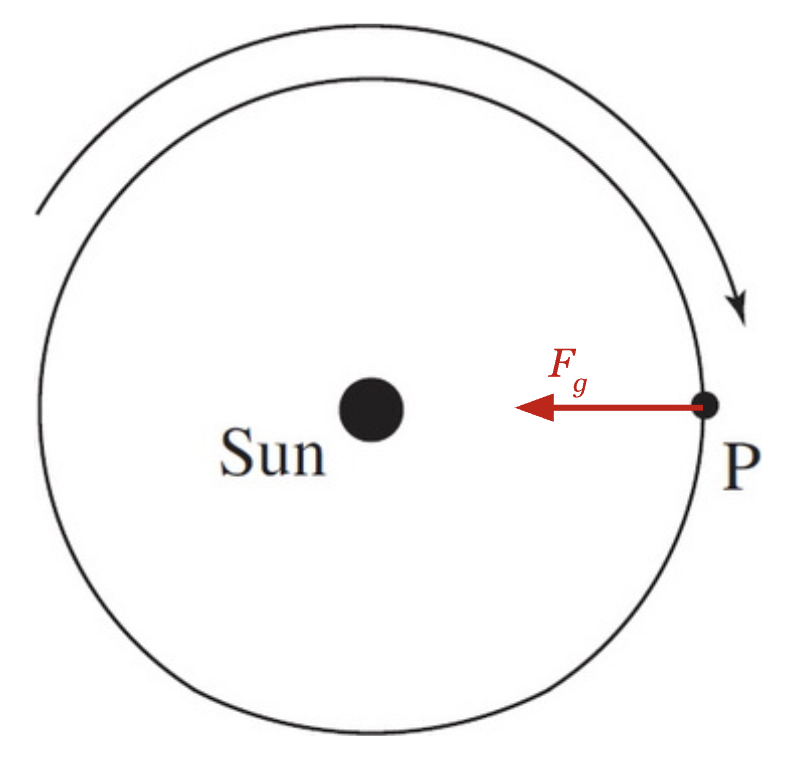
1. Planet Orbiting the Sun

In planetary motion, gravitational force acts as the centripetal force, always pointing toward the center of the orbit.

$$\text{Net Force Equation: }{F}_{\text{net}}=F_g$$

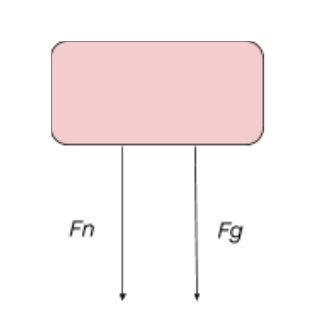
2. Roller Coaster at Different Loop Positions

Top of the Loop

• Forces:
  • Normal Force ($F_n$): Points downward toward the center.
  • Gravitational Force ($F_g$): Points downward.
• Net Force Equation: $$F_{\text{net}}=F_n+F_{\mathrm{g<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}$$

At this position, the apparent weight is less than the actual weight, making riders feel lighter.

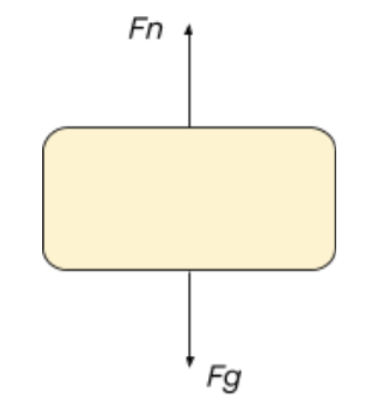
Bottom of the Loop

• Forces:
  • Normal Force ($F_n$): Points upward toward the center.
  • Gravitational Force ($F_g$): Points downward.
• Net Force Equation: $$F_{\text{net}}=F_n-F_{\mathrm{g<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}$$

Here, $F_n > F_g$, meaning riders feel heavier due to the stronger normal force.

Left and Right of the Loop

• Left:

  • Normal Force ($F_n$): Points rightward toward the center.
  • Gravitational Force ($F_g$): Points downward.
  • Net Force Equation: $$F_{\text{net}}=F_n$$

• Right:

  • Normal Force ($F_n$): Points leftward toward the center.
  • Gravitational Force ($F_g$): Points downward.
  • Net Force Equation: $$F_{\text{net}}=F_{\mathrm{n<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}$$

Key Considerations

1. Force Types:

   • Contact Forces: Friction, tension, and normal force.
   • Non-Contact Forces: Gravity.

2. Centripetal Force:

   • Always points toward the center of the circle.
   • Acts as the net force, not a separate force.

3. Apparent Weight:

   • Varies based on the normal force’s magnitude relative to gravity.

Practice Questions

Question 1

What is the direction of the centripetal force for an object in uniform circular motion?

• A) Tangential
• B) Radial (toward the center)
• C) Perpendicular
• D) Downward

Answer: B) Radial (toward the center)

Question 2

At the top of a roller coaster loop, which forces contribute to the net centripetal force?

• A) Normal Force Only
• B) Gravitational Force Only
• C) Both Normal Force and Gravitational Force
• D) Friction

Answer: C) Both Normal Force and Gravitational Force

Question 3

An object in circular motion has a net centripetal force of 50 N acting on it. What happens if the object’s velocity doubles?

• A) The centripetal force halves.
• B) The centripetal force doubles.
• C) The centripetal force quadruples.
• D) The centripetal force remains unchanged.

Answer: C) The centripetal force quadruples.
Explanation: Since $F_c \propto v^2$, doubling the velocity increases the force by $2^2 = 4$.

Key Takeaways

1. Centripetal Force: The net inward force required for circular motion.
2. Free-Body Diagrams: Align the positive axis with the centripetal force for easier analysis.
3. Apparent Weight: Riders feel lighter at the top of loops and heavier at the bottom.