3.6 Centripetal Acceleration and Centripetal Force

Key Concepts and Equations

Centripetal acceleration and force play a central role in circular motion, allowing objects to maintain a curved path.

Important Equations

1. Velocity:

   $$v = \frac{\Delta x}{\Delta t}$$

   ​

2. Acceleration:

   $$a = \frac{\Delta v}{\Delta t}$$

   ​

3. Centripetal Acceleration:

   $$a_c = \frac{v^2}{r}$$

   ​

4. Centripetal Force:

   $$F_c = m \cdot a_c = \frac{m \cdot v^2}{r}$$

   ​

Centripetal Acceleration

Definition:
Centripetal acceleration occurs when an object moves in a circular path, directed toward the center of the circle. This inward acceleration is responsible for changing the direction of the object’s velocity, keeping it in motion along the curved path.

Example:

On a roller coaster loop, you feel pulled toward the center due to centripetal acceleration. The centripetal force responsible for this sensation may come from tension, gravity, friction, or a combination of these forces.

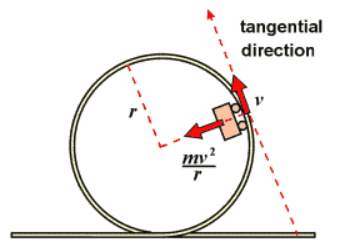
Centripetal vs. Tangential Vectors

• Acceleration Vector: Points toward the center of the circle (radial direction).
• Velocity Vector: Tangent to the circular path, forming a 90-degree angle with the acceleration vector.

This relationship ensures the object maintains a constant speed while continuously changing direction.

Centripetal Force

Definition:
Centripetal force is the net force required to make an object move in a circular path. It acts toward the center of the circle and is not a new force but rather the sum of forces providing the radial acceleration.

Sources of Centripetal Force

• Friction: A car turning on a road.
• Tension: A ball swung in a circle on a string.
• Gravitational Force: Planets orbiting the Sun.

Important Note:

As the speed of an object increases or the radius of the circle decreases, the required centripetal force increases proportionally.

Applications in Physics

1. Uniform Circular Motion

In uniform circular motion, objects move at a constant speed along a circular path, but their velocity changes due to direction changes. Centripetal force keeps them in this motion.

2. Center of Mass

The center of mass (COM) is the average position of an object’s mass distribution. In circular motion, the COM influences the balance and stability of the system.

Practice Questions

Question 1

What is the direction of the centripetal acceleration in uniform circular motion?

• A) Radial
• B) Tangential
• C) Perpendicular
• D) Horizontal

Answer: A) Radial
Explanation: Centripetal acceleration always points toward the center of the circular path.

Question 2

An object of mass 5 kg moves in a circular path with a radius of 3 m and a velocity of 4 m/s. What is the centripetal acceleration?

• A)
  $12 \, \text{m/s}^2$
• B)
  $16 \, \text{m/s}^2$
• C)
  $20 \, \text{m/s}^2$
• D)
  $5.33 \, \text{m/s}^2$

Answer: D)

$5.33 \, \text{m/s}^2$

Explanation:

$$a_c = \frac{v^2}{r} = \frac{(4)^2}{3} = 5.33 \, \text{m/s}^2$$

Question 3

A ball of mass 1 kg tied to a string moves in a circular path of radius 0.5 m with a velocity of 3 m/s. What is the centripetal force acting on the ball?

• A)
  $2.25\text{N}$

   

• B)
  $4.5\text{N}$

   

• C)
  $9\text{N}$

   

• D)
  $1.5 \, \text{N}$

   

Answer: B)

$4.5 \, \text{N}$

Explanation:

$$a_c = \frac{v^2}{r} = \frac{(3)^2}{0.5} = 18 \, \text{m/s}^2$$

$$F_c = m \cdot a_c = 1 \cdot 18 = 18 \, \text{N}$$

Key Takeaways

1. Centripetal acceleration ensures that objects in circular motion stay on their path.
2. Centripetal force is the net inward force that sustains circular motion.
3. Both acceleration and force vectors point toward the center, while the velocity vector is tangent to the circle.