2.7 Applications of Newton’s Second Law: Exploring Motion and Forces

Understanding Linear Motion of a System ➰

In physics, the linear motion of a system is described by the displacement, velocity, and acceleration of its center of mass. When applying Newton’s Second Law, which states:

“The acceleration of an object is directly proportional to the net force acting on it, in the same direction as the net force, and inversely proportional to its mass.”

Essential Variables for Motion:

• Δx: Horizontal displacement (meters)
• Vf: Final velocity (meters/second)
• Vo: Initial velocity (meters/second)
• t: Time (seconds)
• a: Acceleration (m/s²)

Quick Tips for Problem Solving with Newton’s Second Law:

1. Identify the Object of Interest: Pinpoint the object you are analyzing.
2. Create a Free-Body Diagram (FBD): Illustrate all external forces acting on the object.
3. List the Forces: Consider gravitational, frictional, normal, tension, or applied forces.
4. Direction Matters: Assign positive or negative values based on direction.
5. Calculate Force Magnitudes: Use laws such as Newton’s Laws of Motion or conservation principles.
6. Apply $F_{\text{net}} = ma$: Solve for unknowns like acceleration, force, or mass.
7. Verify Your Solution: Ensure units and calculations align with physics principles.

Key Equations for Acceleration 🗯

The relationship between displacement, initial/final velocity, time, and acceleration can be described through kinematic equations, essential when applying Newton’s Second Law to real-world scenarios.

Angular Tension and Apparent Weight 🔊

Angular Tension and Apparent Weight are frequent applications of Newton’s Second Law that challenge students but provide crucial insights into force dynamics.

Understanding Angular Tension

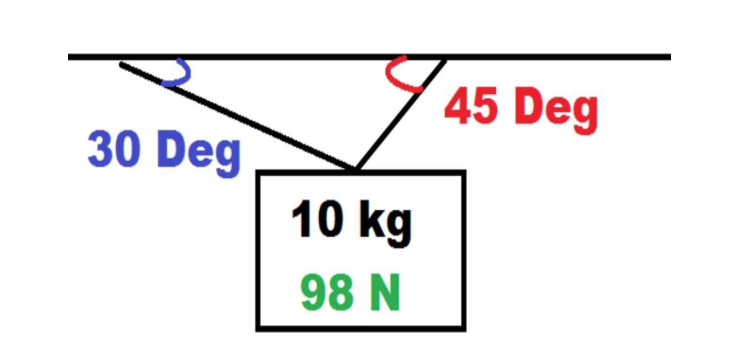
Angular Tension problems arise when an object is suspended by two or more strings at angles. Here’s how to tackle these problems:

1. Draw a Free-Body Diagram (FBD).
2. Identify Forces: Consider all forces, including tension forces, gravity, etc.
3. Determine Force Directions: Most tension forces act along ropes or cables, possibly at angles.
4. Calculate Tension Magnitudes.
5. Apply Physics Principles: Use known forces to solve for unknowns like angles or acceleration.
6. Verify Reasonableness.

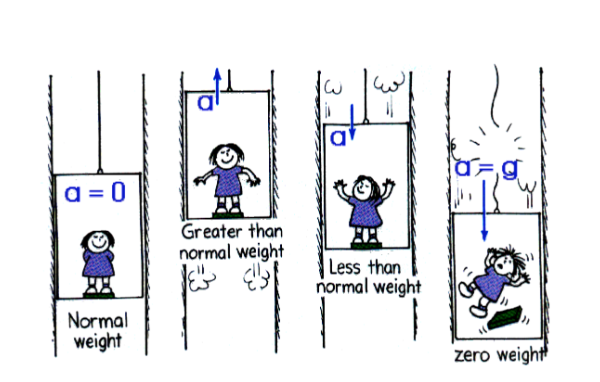
Apparent Weight in Elevators

The apparent weight of an object changes when the force of gravity is not fully balanced by a normal force. Elevator scenarios provide practical examples:

• Upward Acceleration: The floor pushes more forcefully upward, making you feel heavier. $F_{\text{n}} = ma + mg$
• Downward Acceleration: The floor exerts less force, making you feel lighter. $F_{\text{n}} = mg – ma$
• No Acceleration: Apparent weight equals true weight. $F_{\text{n}} = mg$
• Free Fall: No normal force; apparent weight is zero.

Elevator Problem Example

Scenario: You’re in an elevator accelerating upwards.

1. Draw a Free-Body Diagram (FBD).
2. Identify Forces: Include gravitational (downward) and normal forces (upward).
3. Apply Newton’s Second Law: Calculate the net force and apparent weight using: $F_{\text{n}} = ma + mg$

Example Problems and Real-World Applications

Problem 1: Linear Motion of a Box

Given: A box of mass 10 kg is pushed with a 50 N force across a surface with 20 N frictional resistance.

1. FBD Analysis: Rightward force (50 N) and leftward friction (20 N).
2. Net Force Calculation: $F_{\text{net}} = 50\,\text{N} – 20\,\text{N} = 30\,\text{N}$
   
3. Apply Newton’s Second Law: $F_{\text{net}} = ma$
   $30\,\text{N} = 10\,\text{kg} \cdot a$
   $a = 3\,\text{m/s}^2$
   

Problem 2: Apparent Weight in an Elevator

Given: A 60 kg person in an elevator accelerating upward at 2 m/s².

1. Calculate Normal Force: $F_{\text{n}} = ma + mg$
   $F_{\text{n}} = (60\,\text{kg})(2\,\text{m/s}^2) + (60\,\text{kg})(9.8\,\text{m/s}^2)$
   $F_{\text{n}} = 120\,\text{N} + 588\,\text{N} = 708\,\text{N}$
   

Key Takeaways:

• Newton’s Second Law provides the foundation for understanding and calculating how forces affect motion.
• Real-life applications include tension in ropes, apparent weight in elevators, and motion analysis.
• Free-Body Diagrams and a systematic approach make problem-solving manageable.

Frequently Asked Questions (FAQs)

Q: What is the net force on an object in equilibrium?
A: Zero. Objects in equilibrium have balanced forces and do not accelerate.

Q: How does mass affect acceleration?
A: Higher mass reduces acceleration for a given force, as they are inversely proportional.

Q: Why is apparent weight different from actual weight?
A: Apparent weight changes due to acceleration, such as in elevators, while true weight depends solely on mass and gravity.

SEO Keywords

• Newton’s Second Law applications
• Angular tension problems
• Elevator apparent weight physics
• Free-body diagram examples
• Newton’s laws of motion explained