Unit 2.3: Contact Forces in AP Physics 1

Understanding Contact Forces ⛓

In physics, a contact force arises when two objects are physically in contact. This type of force is critical for analyzing motion and interactions between objects. By mastering contact forces, you’ll gain a deeper understanding of how forces like tension, friction, and normal forces shape everyday physical phenomena.

Key Contact Forces

1. Friction
   Friction opposes the motion of an object in contact with a surface, enabling us to walk, grip, and control vehicles. There are two main types:

   • Static Friction: Resists initial movement between surfaces.
   • Kinetic Friction: Opposes motion between moving surfaces.

2. Normal Force
   This force acts perpendicular to a surface, supporting an object’s weight. For example, when sitting in a chair, the chair provides an upward normal force to counteract gravity.

3. Tension
   Tension transmits force along a rope, string, or wire. When you pull on a rope, the tension force transmits that force through the entire length of the rope.

Illustrating Contact Forces in Free-Body Diagrams

When creating free-body diagrams to represent contact forces, keep these principles in mind:

• Tension: Points along the rope or string in the direction of the force being applied.
• Friction: Opposes the direction of motion.
• Normal Force: Always perpendicular to the surface.
• Spring Force: Opposes the direction of compression or extension.

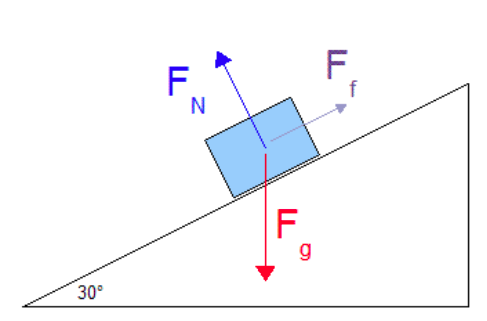
Example: The diagram of an object on an inclined plane demonstrates key forces, including weight (downward), friction (opposing motion), and the normal force (perpendicular to the surface).

Example Problem: Calculating Normal Force

Problem: A 10.0 kg box is placed on a ramp inclined at $30^\circ$ to the horizontal. Calculate the normal force acting on the box.

Solution:

1. Calculate gravitational force: $$F_g = mg = (10.0 \, \text{kg})(9.8 \, \text{m/s}^2) = 98.0 \, \text{N}$$
   
2. Use the normal force equation: $$F_n = F_g \cos \theta = (98.0 \, \text{N}) \cos (30^\circ) = 86.6 \, \text{N}$$
   

The normal force acting on the box is 86.6 N.

Understanding Hooke’s Law

Hooke’s Law describes how the force exerted by a spring is directly proportional to its displacement:

$$F=-kx$$

Where:

• $F$ = force exerted by the spring (N)
• $k$ = spring constant (N/m)
• $x$ = displacement from equilibrium (m)

Note: The negative sign indicates the force is restorative (opposing the displacement).

Example Problem: Calculating Spring Force

Problem: How much force is required to stretch a spring with a spring constant of $10 \, \text{N/m}$ by 20 m?

Solution:

$$F=kx=(10\text{N/m})(20\text{m})=200\text{N}$$

The force required is 200 N.

Exploring Friction

Friction opposes motion or attempted motion of an object in contact with a surface. Frictional force can be calculated using:

$$F_f\le \mu F_{\mathrm{n<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}$$Where:

• $F_f$ = frictional force (N)
• $\mu$ = coefficient of static or kinetic friction
• $F_n$ = normal force (N)

Static vs. Kinetic Friction

• Static Friction: Resists the initial movement of an object. Larger than kinetic friction.
• Kinetic Friction: Acts on moving objects to oppose motion.

Example Problem: Calculating Acceleration on an Inclined Plane

Problem: A 4.00 kg block is placed on a ramp inclined at $30^\circ$ to the horizontal. The coefficient of friction between the block and ramp is $0.400$. Calculate the block’s acceleration as it slides.

Solution:

1. Calculate gravitational force: $$F_g = mg = (4.00 \, \text{kg})(9.81 \, \text{m/s}^2) = 39.24 \, \text{N}$$
   
2. Calculate normal force: $$F_n = F_g \cos \theta = (39.24 \, \text{N}) \cos (30^\circ) = 33.97 \, \text{N}$$
   
3. Calculate frictional force: $$F_f = \mu F_n = (0.400)(33.97 \, \text{N}) = 13.59 \, \text{N}$$
   
4. Calculate the parallel component of gravity: $$F_{\text{parallel}} = mg \sin \theta = (4.00 \, \text{kg})(9.81 \, \text{m/s}^2) \sin (30^\circ) = 19.62 \, \text{N}$$
   
5. Find net force: $$F_{\text{net}} = F_{\text{parallel}} – F_f = 19.62 \, \text{N} – 13.59 \, \text{N} = 6.03 \, \text{N}$$
   
6. Calculate acceleration: $$a = \frac{F_{\text{net}}}{m} = \frac{6.03 \, \text{N}}{4.00 \, \text{kg}} = 1.51 \, \text{m/s}^2$$
   

The block’s acceleration down the ramp is 1.51 m/s².

Key Takeaways on Contact Forces

• Normal Forces support weight and are perpendicular to the contact surface.
• Tension transmits pulling forces.
• Friction resists motion and varies depending on surface conditions.
• Hooke’s Law governs spring force behavior.