Graphs of Inverse trigonometry Functions
Function Name
Parent Function
Graph of Function
Characteristics
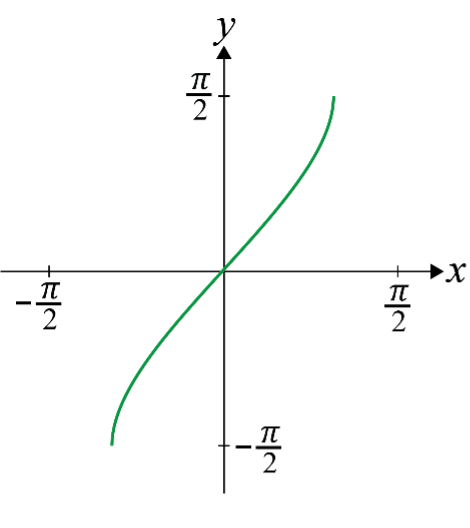
Inverse Sine
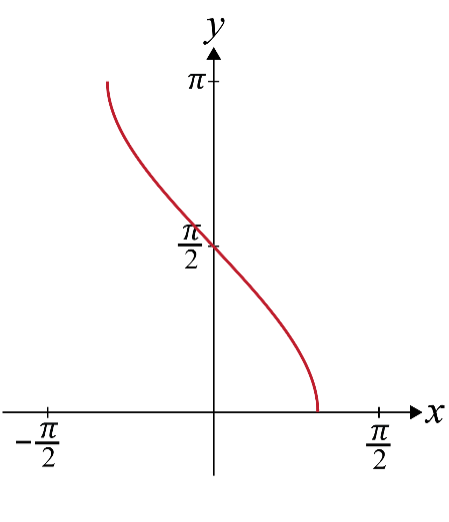
Inverse Cosine
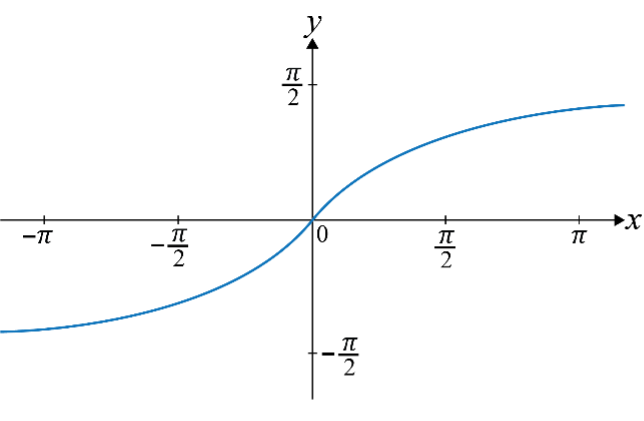
Inverse Tangent
Inverse Cosecant
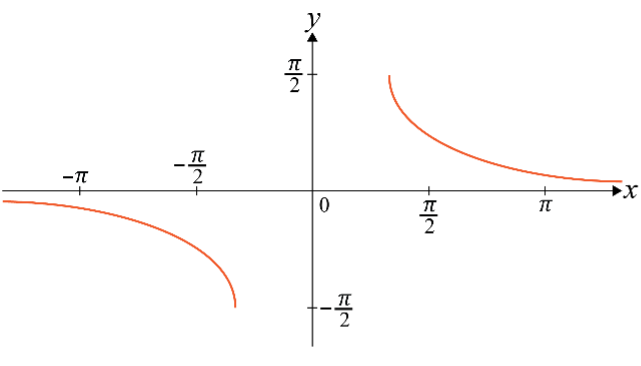
Domain:
Range:
Inverse Secant

Domain:
Range:
Inverse Cotangent
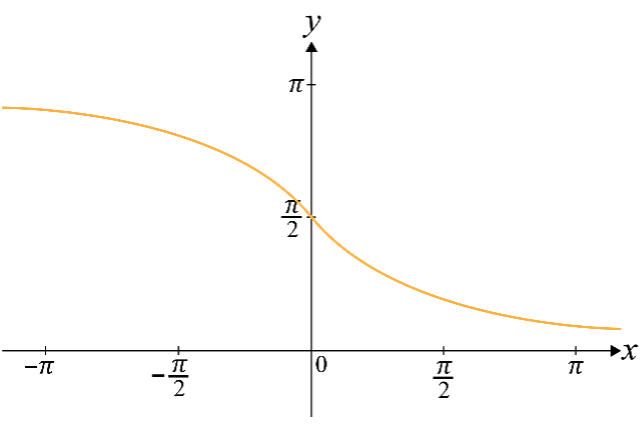
Domain:
Range:
Understanding Inverse Trigonometric Functions
Inverse trigonometric functions allow us to find angles when given specific trigonometric values. They are essential for solving trigonometric equations, modeling periodic phenomena, and are used extensively in calculus. This guide explores the properties, graphs, domains, and ranges of the six major inverse trigonometric functions.
1. Definition and Notation
The inverse trigonometric functions include:
- Inverse Sine (arcsin or ): If , then .
- Inverse Cosine (arccos or ): If , then .
- Inverse Tangent (arctan or ): If , then .
- Inverse Cotangent (arccot or ): If , then .
- Inverse Secant (arcsec or ): If , then .
- Inverse Cosecant (arccsc or ): If , then .
2. Properties of Inverse Trigonometric Functions
Understanding the domain and range of these functions is crucial for their proper application. Let’s explore each in detail:
a. Inverse Sine Function (
- Domain:
- Range:
b. Inverse Cosine Function (
- Domain:
- Range:
c. Inverse Tangent Function (
- Domain:
- Range:
d. Inverse Cotangent Function (
- Domain:
- Range:
e. Inverse Secant Function (
- Domain:
- Range:
f. Inverse Cosecant Function (
- Domain:
- Range:
3. Graphs of Inverse Trigonometric Functions
To visualize how these functions behave, below are clean, graphical representations of each inverse trigonometric function. These graphs show their behavior over their respective domains and ranges.
Insert clean graphs of each function here, focusing on clarity without unnecessary labels.
4. Applications of Inverse Trigonometric Functions
Inverse trigonometric functions appear in many real-world applications:
- Engineering: Signal processing, wave modeling, and solving problems involving angles and distances.
- Physics: Modeling oscillations, pendulums, and wave mechanics.
- Calculus: In calculus, these functions are often encountered in integrals and derivatives.
For example:
- The derivative of is given by:
- The integral of is .
5. Common Mistakes and Tips
- Domain Errors: Ensure values fall within the correct domain.
- Principal Values: Remember that the range of inverse functions is restricted to principal values to ensure that they are functions.
Conclusion
Inverse trigonometric functions are a powerful tool in both mathematics and applied sciences. By understanding their properties, domain, and range, you can unlock their potential in problem-solving and real-world applications.