Arc AB Circle

Understanding Arc Length and Sector Area: A Complete Guide
When working with circles, we often encounter scenarios that require us to calculate the length of an arc or find the area of a sector. Whether you’re studying geometry, preparing for a standardized test, or just looking to expand your mathematical knowledge, understanding these formulas is crucial. This guide will walk you through how to calculate arc length and the area of a sector when angles are provided in degrees or radians.
What Is an Arc?
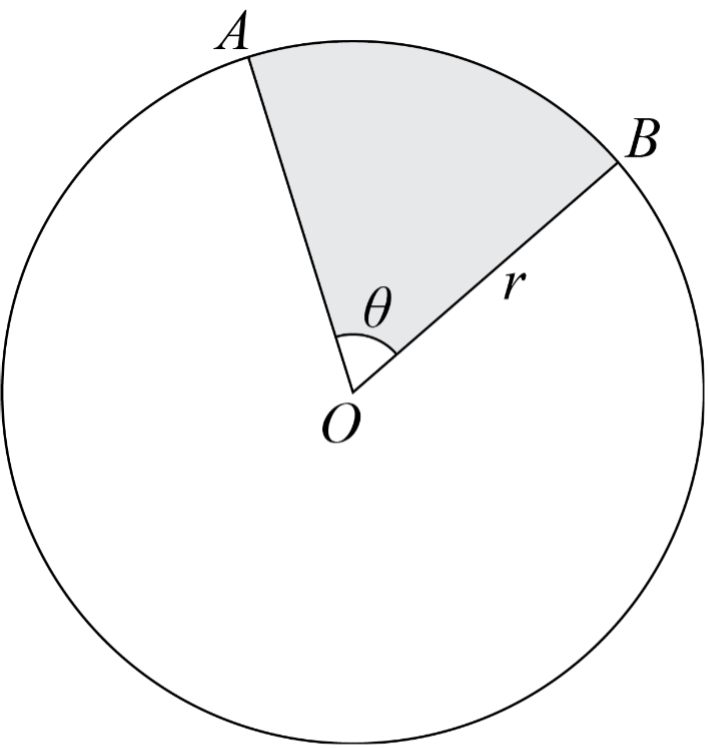
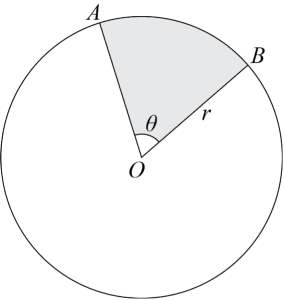
An arc is a portion of the circumference of a circle. The length of this curved line depends on the size of the angle that subtends the arc, measured at the circle’s center.
Arc Length Formula
The formula for finding the arc length varies based on the unit of measurement for the angle:
Arc Length in Degrees
When the central angle, , is in degrees, the formula is given by:
Here:
- “Arc length” is the length of the arc portion
- is the central angle in degrees
- r is the radius of the circle
Arc Length in Radians
When the central angle, , is in radians, the arc length is simpler to calculate:
This formula makes use of the direct proportionality between the angle in radians and the arc length, multiplied by the circle’s radius.
What Is a Sector?
A sector of a circle is the region enclosed by two radii and the arc between them. Imagine a slice of pizza or a pie chart; that’s a sector!
Sector Area Formula
Calculating the area of a sector depends on the unit of the angle measurement:
Sector Area in Degrees
If the central angle, , is measured in degrees, use the formula:
Where:
- “Area” is the area of the sector
- is the central angle in degrees
- is the circle’s radius
Sector Area in Radians
When the central angle is given in radians, the formula becomes:
Example Problems to Illustrate the Concepts
Example 1: Calculating Arc Length
Suppose we have a circle with a radius of 10 cm and a central angle of 45 degrees. To find the arc length:
- Use the formula for arc length in degrees:
- Substitute the values:
Example 2: Finding Sector Area
Given a circle with a radius of 12 cm and a central angle of radians:
- Use the formula for sector area in radians:
- Substitute the values:
Why These Formulas Matter
Understanding arc length and sector area calculations is crucial in various fields such as architecture, engineering, and everyday applications like measuring distances or designing circular objects. Whether dealing with degrees or radians, knowing how to use these formulas empowers you to solve problems efficiently.
Closing Thoughts
Mastering these mathematical concepts might seem daunting initially, but with practice, they become second nature. The formulas for arc length and sector area are not just academic exercises—they have practical applications that you can encounter in real life, from calculating paths on a circle to designing curved objects.
Have any questions or need more examples? Leave a comment below or explore more articles on slyacademy.com for in-depth mathematical explanations and tutorials!