Variance Calculator Use Online Free
Calculate population and sample variance, standard deviation, and mean.
Whole population variance calculation
Population mean:
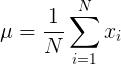
Population variance:
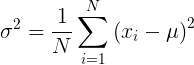
Sampled data variance calculation
Sample mean:
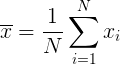
Sample variance:
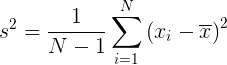
Discrete random variable variance calculation
Random variable mean:
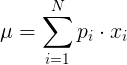
Random variable variance:
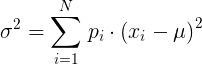
Variance Calculator: Use and Application
A Variance Calculator is a tool that helps you compute the variance of a set of data points. Variance is a key statistical measure that indicates the spread of data points in a dataset. Understanding and calculating variance is fundamental in statistics, data analysis, finance, and various fields where data interpretation is essential.
What is Variance?
Variance measures how much the data points in a dataset deviate from the mean (average) of the dataset. It gives you an idea of the degree of variation within your data. The formula for variance is different depending on whether you’re calculating it for an entire population or a sample of a population:
Population Variance:
Where:
- is the population variance.
- N is the number of data points in the population.
- is each individual data point.
- is the population mean.
Sample Variance:
Where:
- is the sample variance.
- is the number of data points in the sample.
- is each individual data point.
- is the sample mean.
How to Use the Variance Calculator
A Variance Calculator typically includes the following steps:
Input Your Data:
- Enter the data points into the calculator. These can be values from an entire population or a sample from that population. The data is usually input as a list, with values separated by commas or spaces.
Select Data Type:
- Choose whether your data represents the entire population or just a sample. This selection will determine which formula the calculator uses to compute the variance.
Calculate:
- Click the “Calculate” button to compute the variance. The calculator will process your data, find the mean, compute the squared deviations from the mean, and then average those squared deviations to find the variance.
View the Results:
- The calculator will display the variance along with related statistical measures like the mean and standard deviation (the square root of the variance).
Applications of Variance
Variance is a critical concept in statistics and has numerous applications across different fields:
1. Statistics and Data Analysis:
- Data Spread: Variance provides insight into how much data points differ from the mean, indicating whether data points are closely clustered or widely spread out.
- Statistical Modeling: Variance is used to assess the variability in data and is a key component in statistical models such as regression analysis.
2. Finance and Investment:
- Risk Assessment: In finance, variance is used to measure the risk associated with an investment. A higher variance in the returns of a stock, for example, suggests greater risk.
- Portfolio Management: Portfolio managers use variance to construct portfolios that balance risk and return by selecting assets that minimize overall variance.
3. Quality Control:
- Process Variability: In manufacturing, variance is used to monitor the consistency of production processes. A low variance indicates that the process is stable, while a high variance might indicate potential issues that need to be addressed.
- Product Reliability: Variance can be used to assess the reliability of products by analyzing the variability in performance or lifespan of products.
4. Education and Research:
- Performance Analysis: Educators and researchers use variance to analyze test scores or research data to understand the spread of performance among students or study participants.
- Experimental Design: In research, variance helps in determining the precision of measurements and the reliability of experimental results.
5. Healthcare and Medicine:
- Clinical Studies: Variance is used in clinical studies to analyze the variability in patient responses to treatments, helping researchers assess the effectiveness and consistency of medical interventions.
- Epidemiology: Public health officials use variance to study the spread of diseases and the effectiveness of interventions across different populations.
6. Sports Analytics:
- Performance Metrics: In sports, variance is used to evaluate the consistency of players or teams. A low variance in a player’s performance statistics might indicate a reliable performer, while a high variance might suggest inconsistency.
- Strategy Development: Coaches and analysts use variance to develop strategies by understanding the variability in performance under different conditions.
Conclusion
The Variance Calculator is a valuable tool in any field that involves data analysis. By calculating the variance, you gain a deeper understanding of the spread and variability within your data, which can inform decision-making, risk assessment, and the development of strategies. Whether you’re a student, researcher, financial analyst, or engineer, understanding and utilizing variance is essential for interpreting data accurately and making informed decisions based on that data.