Angular Momentum and Its Conservation
Angular momentum is one of the most fundamental concepts in physics, governing rotational motion. It is the rotational equivalent of linear momentum and is conserved in isolated systems.
Angular Momentum Calculator
Calculate angular momentum (L = I·ω) by entering the moment of inertia and angular velocity:
Conservation of Angular Momentum
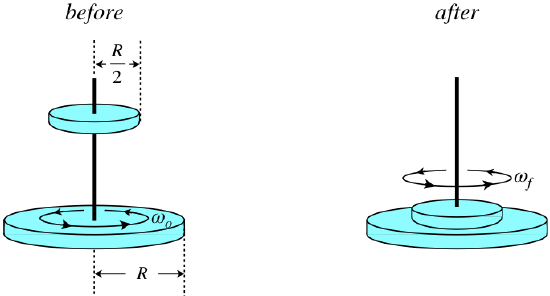
This demonstration shows how angular velocity changes when moment of inertia changes, while angular momentum remains constant.
Drag the radius slider to see how changing the moment of inertia affects angular velocity while angular momentum remains constant (like a figure skater pulling in their arms).
Key Equations in Angular Momentum
Angular Momentum Definition
Where:
- L is the angular momentum (kg·m²/s)
- I is the moment of inertia (kg·m²)
- ω is the angular velocity (rad/s)
Moment of Inertia for Common Shapes
| Object | Moment of Inertia |
|---|---|
| Solid Sphere | I = (2/5)·m·r² |
| Hollow Sphere | I = (2/3)·m·r² |
| Solid Cylinder | I = (1/2)·m·r² |
| Thin Rod (about center) | I = (1/12)·m·l² |
Torque and Angular Momentum Relationship
Conservation of Angular Momentum
When no external torque is applied, angular momentum remains constant. If moment of inertia changes, angular velocity must change in the opposite direction.
Practice Problems
Problem 1: Spinning Satellite
A satellite with a moment of inertia of 10 kg·m² is spinning at 5 rad/s. If the satellite extends its solar panels, increasing its moment of inertia to 15 kg·m², what is its new angular velocity?
Using the conservation of angular momentum:
The satellite's new angular velocity is 3.33 rad/s.
Problem 2: Rotating Disk Collision
Two disks collide on a frictionless surface. Disk A (I = 2 kg·m², ω = 10 rad/s) strikes Disk B (I = 3 kg·m², initially at rest). If the disks stick together, find their final angular velocity.
Conserve angular momentum:
The final angular velocity is 4 rad/s.
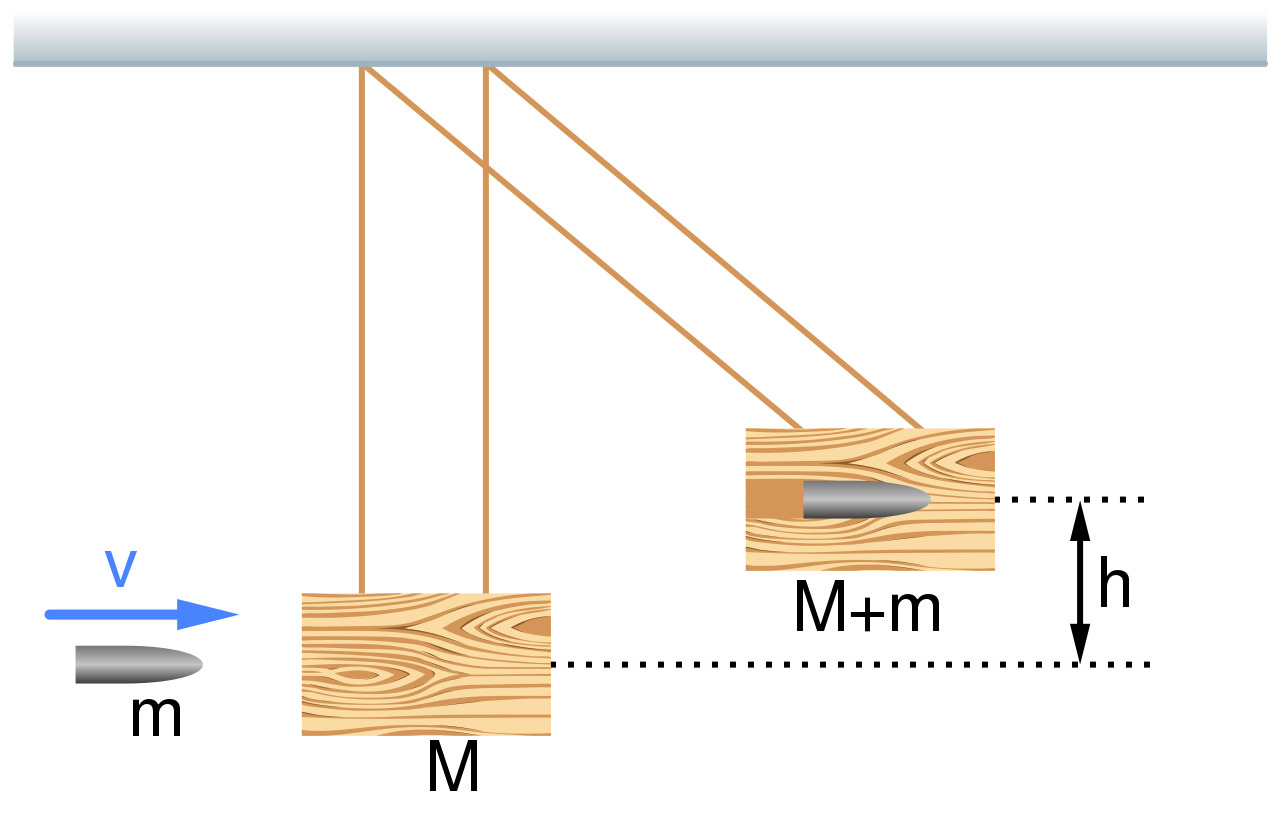
Problem 3: Ballistic Pendulum
A bullet of mass 0.01 kg traveling at 500 m/s embeds itself in a pendulum of mass 2 kg and length 1 m. Calculate the angular velocity of the pendulum immediately after the collision.
Use conservation of angular momentum:
Where:
Plugging in values:
Ever watched a figure skater whip into a lightning-fast spin and thought, “Whoa, how did they just do that?” Or maybe you’ve been mesmerized by a spinning top that defies falling over for minutes. There’s one secret behind all this magic: angular momentum. Stick with me, and you’ll not only understand it—you’ll feel like a rotational rockstar.
What Even Is Angular Momentum?
Let me put it simply: angular momentum is to spinning what linear momentum is to straight-line motion. Think of it as the “oomph” an object has when it’s rotating.
Mathematically, we write it as:
Where:
- L is the angular momentum (measured in
- I is the moment of inertia (a measure of an object’s resistance to changes in rotation)
- ω is the angular velocity (measured in radians per second)
Angular momentum is a vector quantity, meaning it has both magnitude and direction. The direction is determined by the right-hand rule: curl the fingers of your right hand in the direction of the object’s rotation, and your thumb will point in the direction of the angular momentum vector.
Conservation of Angular Momentum
The principle of conservation of angular momentum states:
“The total angular momentum of a system remains constant unless acted upon by an external torque.”
This fundamental law applies to all isolated systems and has profound implications in both classical and quantum physics. Here are some key takeaways about angular momentum conservation:
- Isolated Systems: If no external torques are present, the angular momentum before and after an event remains unchanged.
- Relation to Torque: Torque is the rate of change of angular momentum:
- Impact of Moment of Inertia: When an object’s moment of inertia changes, its angular velocity adjusts to maintain constant angular momentum. For instance, a figure skater pulling their arms in spins faster because their moment of inertia decreases.
Real-World Applications
1. Figure Skaters
When a figure skater pulls their arms closer to their body during a spin, they reduce their moment of inertia. To conserve angular momentum, their angular velocity increases, causing them to spin faster. Conversely, extending their arms slows them down.
2. Spinning Tops and Gyroscopes
A spinning top or gyroscope resists changes to its orientation due to the conservation of angular momentum. This principle is widely used in navigation systems, spacecraft stabilization, and robotics.
3. Colliding Disks
Consider two spinning disks on a frictionless surface. If they collide and stick together, the total angular momentum before and after the collision remains constant. This scenario highlights how angular momentum conservation governs interactions between rotating bodies.
4. Planetary Orbits
Angular momentum conservation plays a crucial role in celestial mechanics. As a planet moves closer to the Sun in its elliptical orbit, its angular velocity increases to conserve angular momentum, and vice versa.
5. Ballistic Pendulum
A ballistic pendulum, used to measure projectile speeds, is a classic example of angular momentum conservation. When a bullet embeds itself into a pendulum, the combined system’s angular momentum before and after the collision remains constant. This principle helps determine the speed of the bullet based on the pendulum’s subsequent motion.
Key Equations in Angular Momentum
Here are the essential equations you need to master angular momentum:
Angular Momentum:
Moment of Inertia for Common Shapes:
- Solid sphere:
- Hollow sphere:
- Solid cylinder:
- Thin rod (about center):
- Solid sphere:
Torque and Angular Momentum Relationship:
Conservation of Angular Momentum:
Practice Problems
1. Spinning Satellite
A satellite with a moment of inertia of
10kg⋅m2 is spinning at
5rad/s. If the satellite extends its solar panels, increasing its moment of inertia to
15kg⋅m2, what is its new angular velocity?
Solution:
Using the conservation of angular momentum:
2. Rotating Disk Collision
Two disks collide on a frictionless surface. Disk A (
I=2kg⋅m2,
ω=10rad/s) strikes Disk B (
I=3kg⋅m2, initially at rest). If the disks stick together, find their final angular velocity.
Solution:
Conserve angular momentum:
3. Ballistic Pendulum
A bullet of mass
0.01kg traveling at
500m/s embeds itself in a pendulum of mass
2kg and length
1m. Calculate the angular velocity of the pendulum immediately after the collision.
Solution:
Use conservation of angular momentum:
Here,
,
, and
.
Plugging in values:
Conclusion
Angular momentum and its conservation offer powerful tools for understanding rotational systems, from everyday objects to celestial mechanics. By mastering these principles, you gain insights into a world governed by symmetry, conservation, and the elegance of rotational motion. Practice applying these concepts to enhance your physics prowess and unravel the mysteries of spinning systems!

Angular Momentum and Its Conservation FAQs
Angular momentum is a vector quantity that represents the rotational equivalent of linear momentum. It is given by: L = Iω where:
- L: Angular momentum,
- I: Moment of inertia,
- ω: Angular velocity.
For a particle, angular momentum is calculated as: L = r × p where:
- L: Angular momentum,
- r: Position vector from the axis of rotation,
- p: Linear momentum of the particle,
- ×: Cross product.
The SI unit of angular momentum is kg·m2/s.
The moment of inertia (I) quantifies an object’s resistance to rotational acceleration. It depends on the mass distribution and axis of rotation: I = Σmr2 where m is the mass and r is the distance of mass from the axis.
The total angular momentum of a closed system remains constant if no external torque acts on it: Linitial = Lfinal.
- Angular momentum: Describes rotational motion.
- Linear momentum: Describes straight-line motion.
Both are conserved in isolated systems.
Torque is the rate of change of angular momentum: τ = dL/dt.
If net external torque is zero, angular momentum remains constant. Otherwise, torque changes angular momentum over time.
In the absence of external torque, an object’s angular momentum remains unchanged, even if its moment of inertia changes.
Figure skaters pulling their arms in to spin faster is a classic example. Reducing their moment of inertia increases their angular velocity while conserving angular momentum.
Planets conserve angular momentum as they orbit the sun. When closer to the sun, their speed increases to maintain constant angular momentum (Kepler's Second Law is a consequence of this).
Angular momentum has two components:
- Orbital angular momentum: Due to motion around a central axis.
- Spin angular momentum: Due to an object’s rotation about its own axis.
Angular momentum explains the rotation of celestial bodies, formation of galaxies (e.g., disk shapes), and orbital dynamics of planets and moons.
Rotational kinetic energy can be expressed as: Krot = L2 / (2I), where L is angular momentum and I is moment of inertia.
The axis of rotation determines the direction of the angular momentum vector. Angular momentum is defined with respect to this axis (or a point), as it depends on the position vector r (from the axis/point) in L = r × p.
In collisions involving rotational motion, if no net external torque acts on the system, the total angular momentum of the system before and after the collision remains constant.
For a rigid body rotating about a fixed axis: L = Iω, where I is the moment of inertia about that axis and ω is the angular velocity.
Gyroscopes maintain their orientation due to the conservation of angular momentum. Their large angular momentum makes them resist changes to their rotational axis when external torques are applied.
Precession is the slow, conical motion of a rotating object’s axis. It is caused by an external torque acting perpendicular to the angular momentum vector, causing the direction of the angular momentum to change over time.
For a point particle with linear momentum p at a position r from the axis (or origin): L = |r||p|sin(θ), where θ is the angle between r and p. Vectorially, L = r × p.
In quantum mechanics, angular momentum (both orbital and spin) is quantized, meaning it can only take on discrete values. It is described by operators, and its eigenvalues determine important properties of particles and atoms, such as energy levels and selection rules for transitions.
In rotational equilibrium, the net external torque on an object is zero (Στ = 0). This implies that the rate of change of angular momentum is zero (dL/dt = 0), so angular momentum remains constant.
For a uniform disk of mass M and radius R rotating about its center axis with angular velocity ω, the moment of inertia is I = (1/2)MR2. Its angular momentum is L = Iω = (1/2)MR2ω.
During galaxy formation, vast clouds of gas and dust collapse under gravity. Assuming negligible external torques, the total angular momentum of the cloud is conserved. As the cloud contracts, its moment of inertia decreases, leading to an increase in its angular velocity (faster rotation) and often resulting in the formation of a flattened disk shape (like spiral galaxies).
For a rigid body rotating about a fixed axis, angular momentum (L) is directly proportional to angular velocity (ω), with the moment of inertia (I) as the constant of proportionality: L = Iω.
In sports like diving, gymnastics, or figure skating, athletes manipulate their body positions to change their moment of inertia (I). By pulling their limbs closer to their body's axis of rotation, they decrease I, which causes their angular velocity (ω) to increase to conserve angular momentum (L), allowing for faster spins or flips.
Spinning tops resist changes to their orientation due to their angular momentum. This gyroscopic effect helps stabilize their motion against gravity. The gravitational torque acting on a tilted top causes precession rather than immediate toppling.
Satellites in orbit conserve angular momentum (assuming no external torques from atmospheric drag or solar wind). This conservation helps maintain stable orbits. For attitude control, reaction wheels are used to change the satellite's orientation by exchanging angular momentum with the wheels.
For a solid sphere of mass M and radius R rotating about an axis through its diameter with angular velocity ω, the moment of inertia is I = (2/5)MR2. Its angular momentum is L = Iω = (2/5)MR2ω.
In an explosion, if the system is isolated (no external torques), the total angular momentum of all fragments after the explosion equals the angular momentum of the system before the explosion. The internal forces of the explosion do not change the total angular momentum of the system.
Rotating black holes (Kerr black holes) possess angular momentum, which is one of their fundamental properties (along with mass and charge). This angular momentum affects the spacetime around the black hole, leading to phenomena like frame-dragging. The angular momentum is typically acquired from the collapsing star or material accreted by the black hole.
Friction (e.g., air resistance, friction in bearings) typically exerts a torque that opposes the rotational motion. This frictional torque causes a change in angular momentum, usually leading to a decrease in angular velocity and eventually slowing down or stopping the rotation.
For a particle of mass m moving in a uniform circular motion with tangential velocity v at a radius r from the center of rotation, its angular momentum magnitude is L = mvr. This is because the position vector r and momentum vector p (mv) are perpendicular (θ = 90°, sin(90°) = 1).
If a rocket expels gases in a way that imparts angular momentum to them (e.g., through angled nozzles or by spinning up a turbine), then by conservation of angular momentum, the rocket itself will gain an equal and opposite angular momentum, assuming no external torques. This principle is used in spin stabilization or to induce rotation.
Earth’s angular momentum has two main components:
- Spin angular momentum: Due to its rotation about its axis (causing day and night).
- Orbital angular momentum: Due to its orbital motion around the Sun.
Both of these are approximately conserved, though tidal forces (especially from the Moon) cause a very slow transfer of angular momentum, slightly slowing Earth's rotation and increasing the Moon's orbital distance.
As a protostellar gas cloud collapses under gravity to form a star, its angular momentum is conserved (assuming isolation). The decrease in size (and thus moment of inertia) causes the cloud to spin faster. This can lead to the formation of a protostellar disk around the young star, from which planets may eventually form.
Spin angular momentum is an intrinsic form of angular momentum carried by elementary particles (like electrons, protons, photons), and composite particles (like atoms). It is a quantum mechanical property not related to actual "spinning" in the classical sense of an object rotating in space. It's quantized and fundamental to particle properties.
The angular momentum of rotating wheels contributes to the stability of vehicles like bicycles and motorcycles through the gyroscopic effect. This effect helps them resist tipping over and makes them easier to balance, especially at higher speeds.
Tidal locking (e.g., the Moon always showing the same face to Earth) is a result of the exchange of angular momentum between a planet and its moon due to tidal forces. Over long periods, this interaction causes the moon's rotation period to match its orbital period, and can also affect the planet's rotation and the moon's orbital distance.
Wind turbines convert the kinetic energy of wind into rotational energy. As wind exerts force on the turbine blades, it imparts a torque, causing them to rotate. The rotating blades possess angular momentum. This mechanical energy is then typically converted into electricity. The design of blades optimizes torque and angular momentum transfer.
Changing the axis of rotation generally changes both the moment of inertia and the angular velocity vector. The angular momentum vector's direction is aligned with the instantaneous axis of rotation for symmetric objects or principal axes. If no external torque acts, the total angular momentum of the system must be conserved, even if its distribution or the orientation of the body changes.
Angular momentum conservation and energy conservation are separate principles. An object's rotational kinetic energy (Krot = L2 / (2I) or Krot = (1/2)Iω2) can change even if angular momentum is conserved (e.g., a figure skater pulling arms in). In this case, work is done to change the moment of inertia, which changes the kinetic energy. Both principles are fundamental in analyzing physical systems.
Figure skaters conserve angular momentum (L = Iω) when spinning (assuming negligible friction from ice). By pulling their arms and legs closer to their body (axis of rotation), they decrease their moment of inertia (I). To keep L constant, their angular velocity (ω) must increase, resulting in a faster spin.
Precession is the change in the orientation of an object's rotational axis. It occurs when an external torque acts on a rotating object with angular momentum. The torque causes the angular momentum vector to change direction over time, tracing a cone-shaped path. A spinning top precessing under gravity is a classic example.
Disk drives (like hard disk drives or CD/DVD drives) rely on the stable and consistent rotation of platters or discs. The conservation of angular momentum helps maintain this constant rotational speed (angular velocity). The gyroscopic effect from the spinning disk also contributes to its stability against minor disturbances.
In particle interactions and decays, total angular momentum (including both orbital and intrinsic spin components) is a conserved quantity. This conservation law helps predict the possible outcomes of reactions, determine the properties (like spin states) of newly discovered particles, and analyze scattering angles.
Robots, especially legged or humanoid robots, use principles of angular momentum for balance and stable movement. They might use reaction wheels, or precisely control limb movements (changing their moment of inertia or generating counter-rotation) to manage their overall angular momentum and maintain stability or perform agile maneuvers.
Galaxies, like the Milky Way, are vast rotating systems. Their overall angular momentum, acquired during their formation from collapsing gas clouds, is largely conserved. This conservation dictates their rotational dynamics, structure (e.g., spiral arms, flat disks), and evolution over billions of years, assuming they are relatively isolated systems.
Angular momentum principles are crucial in many engineering fields. They guide the design of rotating machinery (engines, turbines, flywheels for energy storage), gyroscopes for navigation and stabilization systems (in ships, aircraft, spacecraft), and various control systems that rely on rotational dynamics.
Understanding angular momentum and its conservation is fundamental for analyzing and solving problems across a wide range of physics and engineering disciplines. It is key to explaining phenomena in classical mechanics (like spinning objects and orbits), astronomy (planetary motion, galaxy formation), quantum physics (particle spin, atomic structure), and in designing efficient and stable rotating systems in engineering.







