Circular Motion
Understanding Uniform and Non-Uniform Motion
Overview Circular motion is an essential concept in physics, applicable to both everyday phenomena and advanced scientific studies. From planets orbiting stars to cars navigating curved roads, circular motion governs how objects move in curved paths. In this article, we’ll dive deep into the principles of uniform circular motion (UCM) and its variations, focusing on the forces at play and their implications.
What is Uniform Circular Motion?
Uniform Circular Motion (UCM) refers to the motion of an object traveling in a circular path at a constant speed. While the speed remains constant, the object’s velocity continuously changes because velocity is a vector quantity—it includes both magnitude (speed) and direction. The continuous change in direction means there is always acceleration acting toward the center of the circle, known as centripetal acceleration.
Key Characteristics of UCM:
Velocity: Always tangent to the circle and constantly changing direction.
Centripetal Acceleration: Directed toward the center of the circle.
Centripetal Force: The net force responsible for maintaining circular motion, directed inward.
The relationship among these variables can be expressed mathematically as:
Where:
: Centripetal force
: Centripetal acceleration
: Mass of the object
: Tangential velocity
: Radius of the circular path
Angular Velocity
In addition to linear motion, circular paths can also be described using angular velocity, which measures how quickly an object rotates around a center point.
Where:
: Angular velocity
: Period (time for one full revolution)
Vector Relationships in Circular Motion
Understanding the directions of various vectors is crucial in circular motion:
Centripetal Force: Always points toward the center of the circle.
Centripetal Acceleration: Also directed inward.
Tangential Velocity: Perpendicular to the radius and directed along the tangent of the circle.
These vectors interact to maintain the object’s circular trajectory. For example, while centripetal force pulls the object inward, tangential velocity keeps it from spiraling into the center.
Non-Uniform Circular Motion
When the speed of an object in circular motion varies, the motion is classified as non-uniform circular motion. Here, both tangential and centripetal accelerations come into play.
Key Formulas for Non-Uniform Motion
Total acceleration combines centripetal and tangential components:
Where:
: Tangential acceleration, representing changes in speed.
: Centripetal acceleration, associated with changes in direction.
Applications of Non-Uniform Motion
Non-uniform circular motion is often observed in amusement park rides, satellites adjusting orbits, and vehicles accelerating or decelerating on curved roads.
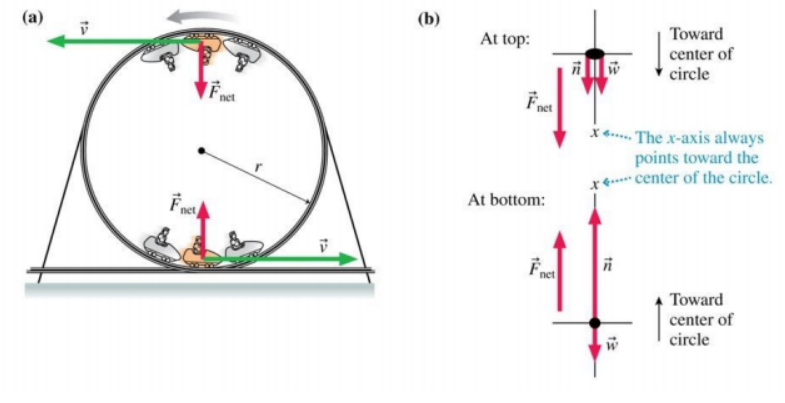
Vertical Circles
Vertical circular motion is a special case of circular motion where gravitational force interacts with centripetal force. This is common in scenarios like roller coasters or pendulums.
Critical Speed
At the top of a vertical loop, the minimum speed required to maintain circular motion is called the critical speed. Here, gravitational force contributes to the centripetal force.
Where:
: Radius of the loop
: Acceleration due to gravity
Forces at Different Points in a Vertical Loop
At the top of the loop: Net force equals the sum of gravitational and normal forces.
At the bottom of the loop: Normal force is greater due to gravity acting in the opposite direction of the centripetal force.
Banked Curves
Banked curves are designed to help vehicles navigate turns without relying solely on friction. The incline provides additional centripetal force, reducing the risk of skidding.
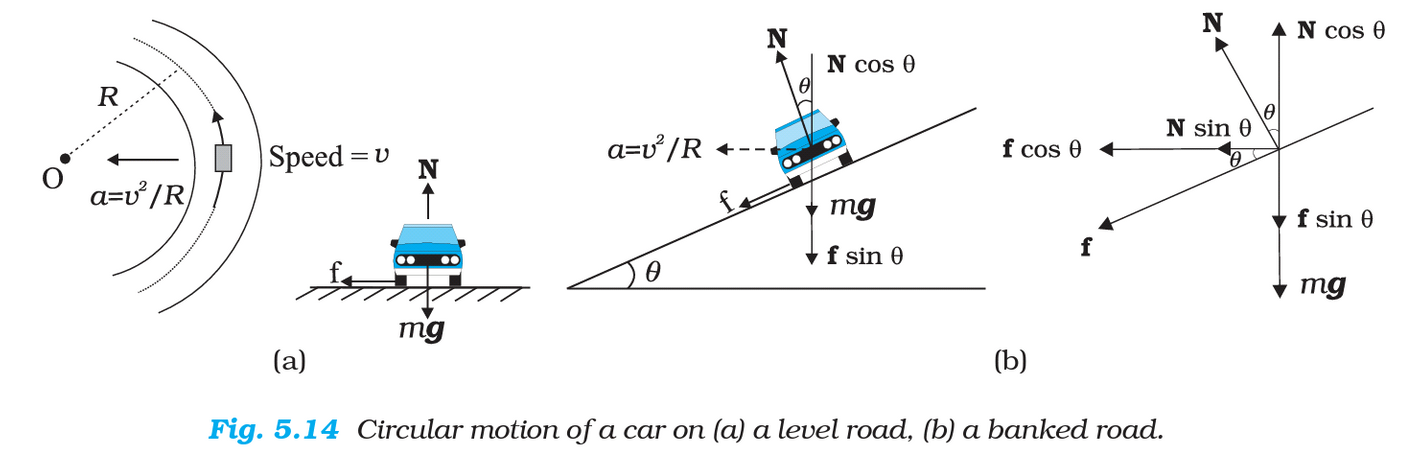
Key Equations for Banked Curves
For an ideal banked curve (no friction):
For a banked curve with friction:
Where:
: Banking angle
: Coefficient of static friction
: Speed of the vehicle
: Radius of the curve
: Gravitational acceleration
Real-Life Applications of Circular Motion
Astronomy:
Orbits of planets, moons, and satellites follow principles of circular motion, governed by gravitational centripetal force.
Amusement Parks:
Rides like Ferris wheels and roller coasters rely on vertical and horizontal circular motion to create thrilling experiences.
Transportation:
Highways and racetracks use banked curves to ensure safety and stability for vehicles navigating turns.
Technology:
Centrifuges use circular motion to separate substances based on density by generating high centripetal force.
Conclusion
Circular motion, whether uniform or non-uniform, is a fundamental aspect of physics that underpins many natural and engineered systems. From understanding the forces at play in a roller coaster loop to the principles behind safe highway design, mastering these concepts is essential for both academic and practical applications. By applying Newton’s laws in the context of circular motion, students can solve complex problems and appreciate the elegance of physics in action.
Circular Motion FAQs
1. What is circular motion?
Circular motion refers to the movement of an object along the circumference of a circle. It can be uniform (constant speed) or non-uniform (changing speed).
2. What is uniform circular motion?
Uniform circular motion occurs when an object moves around a circular path at a constant speed. While the speed is constant, the direction of motion changes continuously.
3. What is non-uniform circular motion?
Non-uniform circular motion occurs when an object’s speed along the circular path changes. This results in both tangential and centripetal accelerations.
4. What are the key parameters of circular motion?
Key parameters include:
Radius (r): Distance from the center to the moving object.
Tangential velocity (v): Speed along the circular path.
Angular velocity (ω): Rate of rotation.
Centripetal acceleration (a_c): Acceleration directed toward the center.
5. What is centripetal force?
Centripetal force is the inward force required to keep an object moving in a circular path. It is given by: where:
is mass,
is tangential velocity,
is radius.
6. What is tangential velocity?
Tangential velocity is the linear speed of an object moving along a circular path. It is given by: where is angular velocity.
7. What is angular velocity?
Angular velocity is the rate at which an object rotates or revolves around the center of a circle. It is measured in radians per second (rad/s).
8. What is the relationship between angular velocity and tangential velocity?
Tangential velocity (v) is related to angular velocity () by: where is the radius.
9. What is centripetal acceleration?
Centripetal acceleration is the acceleration directed toward the center of the circular path. It is given by: or
10. What is the difference between centripetal and centrifugal forces?
Centripetal force: Real force directed toward the center of the circular path.
Centrifugal force: Apparent force experienced in a rotating frame, directed outward.
11. How do you calculate the period of circular motion?
The period (T) is the time taken for one complete revolution. It is given by: or
12. How do you calculate the frequency of circular motion?
Frequency (f) is the number of revolutions per second. It is the reciprocal of the period:
13. What is the formula for angular displacement?
Angular displacement (Θ) is given by: where is the time.
14. What is the relationship between linear and angular quantities?
Key relationships include:
15. What is radial acceleration?
Radial acceleration is another term for centripetal acceleration, directed toward the center of the circular path.
16. What is tangential acceleration?
Tangential acceleration occurs when the speed of an object in circular motion changes. It is given by:
17. How is total acceleration calculated in non-uniform circular motion?
Total acceleration () is the vector sum of tangential () and centripetal () accelerations:
18. What is the centripetal force in a banked curve?
For a car on a banked curve, centripetal force is provided by the horizontal component of the normal force and friction.
19. What is the angle of banking in circular motion?
The angle of banking () is given by: where is the acceleration due to gravity.
20. What is the Coriolis effect?
The Coriolis effect is an apparent deflection of moving objects in a rotating frame of reference, caused by Earth’s rotation.
21. How does circular motion apply to satellites?
Satellites in orbit experience centripetal force due to gravity, keeping them in circular paths around Earth.
22. What is orbital velocity?
Orbital velocity is the velocity required for an object to stay in circular orbit. It is given by: where is the gravitational constant and is the mass of the central body.
23. What is the tension in a string during circular motion?
The tension in the string provides the centripetal force required for circular motion:
24. How is energy conserved in circular motion?
In uniform circular motion, kinetic energy remains constant, while potential energy may vary depending on the system (e.g., vertical loops).
25. What is the difference between rotation and revolution?
Rotation: Motion around an internal axis (e.g., Earth spinning on its axis).
Revolution: Motion around an external axis (e.g., Earth orbiting the Sun).
26. How do vertical loops affect circular motion?
In vertical loops, the centripetal force is provided by the tension in the string and gravity. Forces vary depending on the object’s position in the loop.
27. What is the role of friction in circular motion?
Friction provides the centripetal force needed for circular motion in scenarios like cars turning on flat roads.
28. How does circular motion apply to amusement park rides?
Circular motion explains the operation of rides like Ferris wheels and roller coasters, involving centripetal forces and acceleration.
29. What is the significance of radius in circular motion?
The radius determines the curvature of the path and affects tangential velocity, centripetal acceleration, and period.
30. How is angular momentum related to circular motion?
Angular momentum () is given by: where is the moment of inertia and is angular velocity. It is conserved in the absence of external torques.
31. How does gravity affect circular motion?
Gravity provides the centripetal force for objects like planets and satellites in circular orbits.
32. How does mass affect circular motion?
Mass affects the centripetal force required to maintain circular motion:
33. What is the relationship between frequency and angular velocity?
Frequency () and angular velocity () are related by:
34. How do you calculate work done in circular motion?
In uniform circular motion, no work is done by the centripetal force because it acts perpendicular to the displacement.
35. What is the moment of inertia in circular motion?
Moment of inertia () is the resistance to rotational motion, depending on the mass distribution relative to the axis of rotation.
36. How does tension affect circular motion?
Tension in a string or rope provides the necessary centripetal force to maintain circular motion.
37. What is the role of torque in circular motion?
Torque causes rotational motion and changes angular momentum. It is given by:
38. How does circular motion differ from linear motion?
Circular motion involves constant changes in direction, while linear motion occurs in a straight line with constant direction.
39. What is a gyroscope, and how does it relate to circular motion?
A gyroscope is a device that uses angular momentum to maintain orientation. Its behavior is governed by the principles of circular motion and rotation.
40. What is the principle of centripetal force?
Centripetal force is essential for maintaining circular motion, acting perpendicular to the object’s tangential velocity.
41. How do centrifugal forces arise?
Centrifugal forces are apparent forces experienced in a rotating frame, perceived as acting outward due to inertia.
42. How do banked roads aid circular motion?
Banked roads reduce reliance on friction by providing a normal force component that contributes to the centripetal force.
43. What is the role of angular displacement in circular motion?
Angular displacement measures the angle traversed by an object in circular motion, providing a basis for calculating angular velocity and acceleration.
44. How does circular motion apply to planetary orbits?
Planetary orbits are governed by gravitational centripetal force, balancing the tangential velocity of planets.
45. How does air resistance affect circular motion?
Air resistance opposes motion, reducing tangential velocity and requiring additional force to maintain circular motion.
46. What is the relationship between centripetal force and angular velocity?
Centripetal force is proportional to the square of angular velocity:
47. How do rotating systems achieve stability?
Rotating systems achieve stability through conservation of angular momentum and balanced forces.
48. How does tension vary in vertical circular motion?
In vertical circular motion, tension is greatest at the bottom of the path and smallest at the top due to the combined effects of gravity and centripetal force.
49. What is the conservation of angular momentum in circular motion?
Angular momentum remains constant in a closed system unless acted upon by an external torque.
50. How does circular motion apply to real-world scenarios?
Circular motion is fundamental in:
Engineering (e.g., gears, turbines).
Space exploration (e.g., satellite orbits).
Sports (e.g., discus throwing).
Transportation (e.g., turning vehicles).
2.3 Newton's Laws of Motion: Third Law
2.1 Newton's Laws of Motion: First and Second Law
Unit 2 Overview: Newton’s Laws of Motion
7.2 Considering how words, phrases, and clauses can modify and limit an argument
7.1 Examining complexities in issues
Unit 7 Overview: Successful and Unsuccessful Arguments
