4.4 Biot Savart Law and Amperes Law
Comprehensive Guide
Magnetic fields play a crucial role in understanding electromagnetism, and two cornerstone principles—the Biot-Savart Law and Ampère’s Law—help calculate magnetic fields for various configurations. This guide explores these laws in depth, detailing their applications, derivations, and practical use cases in solenoids, coaxial cables, and loops of wire.
Biot-Savart Law
The Biot-Savart Law allows us to calculate the magnetic field at a point in space due to a current-carrying wire. By breaking the wire into infinitesimal segments, we can sum the contributions of each segment to the total magnetic field.
The law is expressed as:
Where:
: Infinitesimal magnetic field (T)
: Permeability of free space ( N/A)
: Current through the wire (A)
: Infinitesimal length of the wire (m)
: Unit vector pointing from the wire to the point of interest
: Distance from the wire segment to the point of interest (m)

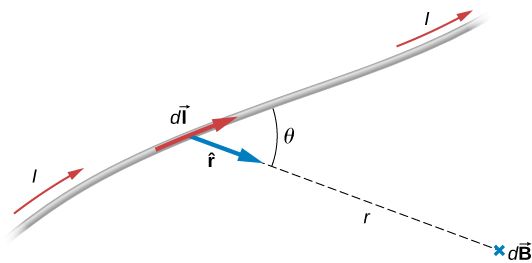
Common Geometries for Using Biot-Savart Law
1. Magnetic Field at the Center of a Loop
For a circular current-carrying loop, the magnetic field at the center is:
Where is the radius of the loop. Symmetry ensures that contributions from all parts of the loop sum up in the same direction.
2. Magnetic Field Along the Axis of a Loop
On the axis of a circular loop:
Where is the distance along the axis from the center of the loop.
3. Magnetic Field of an Infinite Straight Wire
For an infinitely long, straight wire:
Where is the perpendicular distance from the wire to the point of interest.
Ampère’s Law
Ampère’s Law simplifies magnetic field calculations for symmetrical systems. It states:
Where:
: Line integral of the magnetic field along a closed path
: Current enclosed by the path

Applications of Ampère’s Law
1. Coaxial Cables
Consider two concentric cylindrical conductors with currents flowing in opposite directions. The magnetic field at different radii is:
:
Magnetic field is proportional to the enclosed current.
:
Encloses the full current in the inner conductor.
:
Encloses the current in the inner conductor minus the current in the outer conductor.
:
Encloses equal and opposite currents; net magnetic field is zero.
2. Solenoids
A solenoid is a tightly wound coil of wire that generates a uniform magnetic field when current flows through it. The field inside a solenoid is given by:
Where:
: Number of turns per unit length
: Current through the solenoid
To determine the field using Ampère’s Law:
Choose a rectangular Amperian loop enclosing turns.
Integrate along the loop to find.

Solenoids in Practice
Solenoids have numerous practical applications, from car engines to electromagnets used in scientific research. Using the right-hand curl rule, you can determine the direction of the magnetic field:
Curl your fingers in the direction of the current.
Your thumb points in the direction of the magnetic field.
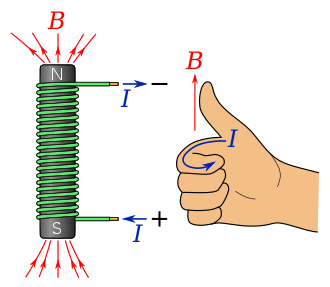
Example: A solenoid with 500 turns per meter carrying a 2A current produces a magnetic field:
Practice Problem Examples
Problem 1: Magnetic Field at the Center of a Loop
A circular loop of radius carries a current . If the radius doubles to , what happens to the magnetic field at the center?
Solution: From Biot-Savart Law:
Doubling reduces by half.
Problem 2: Magnetic Field in a Solenoid
A solenoid with radius , length , and total turns carries current . Determine the magnetic field at the center.
Solution:
Use Ampère’s Law:
Simplify to find at the center:
Key Takeaways
Biot-Savart Law:
Best for calculating fields in non-symmetrical systems.
Useful for loops, arcs, and finite wires.
Ampère’s Law:
Ideal for symmetrical systems like solenoids and coaxial cables.
Relates magnetic fields to enclosed current.
Practical Applications:
Solenoids create uniform magnetic fields for use in devices like car starters and MRI machines.
Coaxial cables minimize external magnetic fields by canceling opposing currents.
Biot–Savart Law and Ampère’s Law FAQs
1. What is the Biot–Savart Law?
The Biot–Savart Law describes the magnetic field generated by a steady electric current. It states that the magnetic field (→B) at a point in space is proportional to the current (→I), the length element (→dl), and inversely proportional to the square of the distance (→r) between the point and the current-carrying wire. Mathematically:
where:
μ₀ is the permeability of free space.
is the infinitesimal current element vector.
is the unit vector from the current element to the point of observation.
2. What is Ampère’s Law?
Ampère’s Law relates the magnetic field around a closed loop to the electric current passing through the loop. It is given by:
where:
is the line integral of the magnetic field along a closed loop.
is the net current passing through the loop.
μ₀ is the permeability of free space.
3. How are Biot–Savart Law and Ampère’s Law related?
The Biot–Savart Law provides the magnetic field due to a current element, while Ampère’s Law provides the relationship between the magnetic field and the total current enclosed in a loop. Ampère’s Law can be derived from the Biot–Savart Law under certain symmetry conditions.
4. What are the applications of the Biot–Savart Law?
Applications include:
Calculating the magnetic field of current loops.
Determining the field of long, straight wires.
Analyzing magnetic fields in circular coils.
Studying electromagnetic waves.
5. What are the applications of Ampère’s Law?
Applications include:
Magnetic field of solenoids.
Magnetic field of toroids.
Verification of Maxwell’s equations.
Magnetic field inside and outside current-carrying conductors.
6. What is the significance of μ₀ in these laws?
μ₀, or the permeability of free space, is a fundamental physical constant that defines the relationship between magnetic fields and electric currents in a vacuum. Its value is:
7. How is the Biot–Savart Law derived?
The Biot–Savart Law is derived from the experimental observation that a small current element produces a magnetic field, which follows the inverse-square law and is perpendicular to both the current and the radial vector.
8. Can Biot–Savart Law be used for moving charges?
Yes, the Biot–Savart Law can be extended to moving charges. The magnetic field (→B) due to a moving charge q with velocity (→v) is given by:
9. Why is Ampère’s Law important in electromagnetism?
Ampère’s Law provides a simplified method to calculate magnetic fields in systems with high symmetry and plays a crucial role in the formulation of Maxwell’s equations, which describe all classical electromagnetic phenomena.
10. What are the limitations of the Biot–Savart Law?
It assumes steady currents and cannot be directly applied to time-varying currents.
Difficult to apply in systems without symmetry.
Requires numerical integration for complex geometries.
11. What are the limitations of Ampère’s Law?
Requires symmetry for straightforward application.
Only applicable to static or quasi-static fields.
Does not account for displacement current unless Maxwell’s correction is included.
12. How does Ampère’s Law explain the magnetic field inside a solenoid?
Using Ampère’s Law for a solenoid with n turns per unit length and current I, the magnetic field inside is:
13. How is the Biot–Savart Law used for a circular loop?
The magnetic field at the center of a circular loop with radius R and current I is:
14. Can Ampère’s Law be used for non-symmetric systems?
No, Ampère’s Law is most effective in systems with symmetry, such as straight wires, solenoids, or toroids. For non-symmetric systems, the Biot–Savart Law is more appropriate.
15. What is the displacement current in Ampère’s Law?
The displacement current is a term added by Maxwell to Ampère’s Law to account for time-varying electric fields. The modified law is:
where is the rate of change of electric flux.
16. How does the Biot–Savart Law apply to magnetic dipoles?
The Biot–Savart Law can be used to calculate the magnetic field of a current loop, which acts as a magnetic dipole at large distances.
17. How does Ampère’s Law relate to Faraday’s Law?
Ampère’s Law (with Maxwell’s correction) complements Faraday’s Law in Maxwell’s equations, linking electric and magnetic fields in time-varying systems.
18. Can Biot–Savart Law be used to derive Ampère’s Law?
Yes, by integrating the Biot–Savart Law around a closed loop and using symmetry, Ampère’s Law can be derived.
19. What are the key assumptions in the Biot–Savart Law?
Steady current.
Magnetic effects dominate over electric effects.
Point-like observation of magnetic fields.
20. Is Ampère’s Law valid for time-varying fields?
Not in its original form. Maxwell’s correction, introducing the displacement current, extends its validity to time-varying fields.
21. How does the Biot–Savart Law describe magnetic fields near a straight wire?
The magnetic field at a distance r from an infinitely long straight wire is:
22. What is the role of Ampère’s Law in Maxwell’s equations?
It provides the foundation for describing how magnetic fields are generated by currents and changing electric fields.
23. How does the Biot–Savart Law explain the magnetic field of a current element?
It shows that the magnetic field is proportional to the cross product of the current element and the distance vector, scaled by the inverse square of the distance.
24. What is the differential form of Ampère’s Law?
where is the current density.
25. Can Ampère’s Law be used in a vacuum?
Yes, it applies in a vacuum, provided the displacement current term is included.
26. What are the practical uses of the Biot–Savart Law?
It is widely used in designing electromagnets, understanding magnetic fields in circuits, and analyzing fields in particle accelerators.
27. How does Ampère’s Law apply to toroids?
For a toroid with N turns, radius R, and current I:
28. What are the advantages of Ampère’s Law over the Biot–Savart Law?
Simplicity in symmetric systems.
Requires less computation for closed-loop integrals.
29. What are the disadvantages of Ampère’s Law?
Inefficient for non-symmetric systems.
Requires Maxwell’s correction for time-varying fields.
30. How is Ampère’s Law verified experimentally?
Through magnetic field measurements around conductors and solenoids, confirming the proportionality to current.
31. What is the historical origin of the Biot–Savart Law?
It was formulated by Jean-Baptiste Biot and Felix Savart in 1820 based on their experiments on magnetic effects of electric currents.
32. How is Ampère’s Law used in electromagnetic wave theory?
It explains the magnetic component of electromagnetic waves and their propagation.
33. Can the Biot–Savart Law be applied to surface currents?
Yes, by integrating over the current distribution on the surface.
34. Why is Ampère’s Law simpler for solenoids?
The symmetry of solenoids allows direct application of Ampère’s Law without requiring complex integrations.
35. How does the Biot–Savart Law apply to helical coils?
It requires integration over the helical path to compute the magnetic field.
36. What is the significance of the cross product in the Biot–Savart Law?
The cross product ensures the magnetic field is perpendicular to both the current element and the radial vector.
37. What units are used in the Biot–Savart Law?
The magnetic field (→B) is measured in teslas (T).
38. Is Ampère’s Law used in computational electromagnetics?
Yes, it simplifies field calculations in finite element and boundary element methods.
39. How does the Biot–Savart Law explain magnetic field lines?
The law shows that magnetic field lines are circular around current-carrying wires.
40. What is the Ampère-Maxwell Law?
It is Ampère’s Law with Maxwell’s correction, accounting for displacement current:
41. What is the role of symmetry in Ampère’s Law?
Symmetry simplifies the evaluation of magnetic fields, making Ampère’s Law more effective.
42. Can the Biot–Savart Law handle multiple currents?
Yes, by superposition, the magnetic fields due to individual currents are summed.
43. What is the role of Ampère’s Law in circuit analysis?
It helps compute magnetic fields around circuits, aiding in inductance and field strength calculations.
44. How does the Biot–Savart Law apply to infinite sheets of current?
The integration yields a uniform magnetic field above and below the sheet.
45. Can Ampère’s Law predict magnetic field directions?
Yes, using the right-hand rule.
46. How does the Biot–Savart Law apply to magnetic dipoles?
At large distances, the field resembles that of a dipole, decaying as .
47. What are the experimental validations of Ampère’s Law?
Measurements of solenoids, toroids, and magnetic flux densities confirm its validity.
48. Why is the Biot–Savart Law not used for complex systems?
It involves intricate integrations, making it computationally intensive.
49. What is the significance of the line integral in Ampère’s Law?
It quantifies the magnetic field circulation around a loop.
50. How do Biot–Savart Law and Ampère’s Law complement each other?
The Biot–Savart Law provides detailed field calculations for small elements, while Ampère’s Law offers a global perspective on the field generated by currents.







