7.7 Wave Functions and Probability

Wave Functions and Probability: Exploring Quantum Mechanics

Introduction

In the world of quantum mechanics, the behavior of particles is fundamentally different from classical predictions. The wave function, a core concept in quantum theory, provides a probabilistic description of matter. It is a mathematical function that describes the motion and interactions of a particle in space and time, offering insights into the particle’s quantum state.

This article delves into the anatomy of wave functions, their relation to probability, and their implications in quantum systems. We also explore their role in understanding phenomena such as electron energy states, standing waves, radioactive decay, and photon interactions.

What is a Wave Function?

The wave function, often denoted by ψ(x, t), is a complex-valued function in quantum mechanics that encodes all the information about a particle’s quantum state. Its square, |ψ(x, t)|², represents the probability density, or the likelihood of finding the particle at a given position and time.

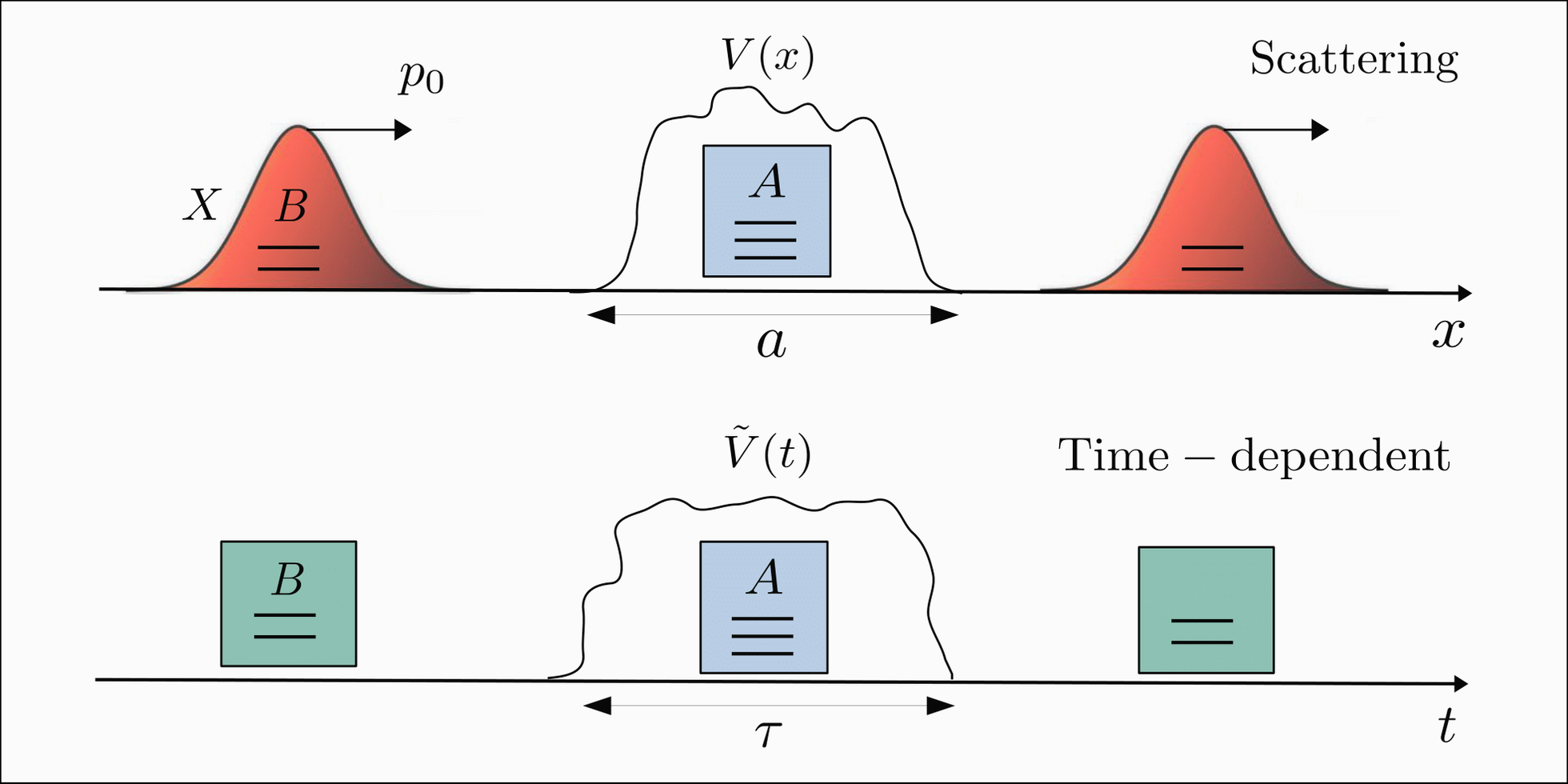
Key Features of the Wave Function:

1. Complex Nature:

   • The wave function can have both real and imaginary components, allowing for rich descriptions of quantum systems.

2. Probabilistic Interpretation:

   • The absolute square of the wave function, |ψ(x, t)|², gives the probability density.

3. Normalization:

   • The total probability of finding the particle across all space is 1, ensuring the wave function is normalized: ∫ |ψ(x, t)|² dx = 1.

Graphical Representation of Wave Functions

Visualizing wave functions helps in understanding probability density distributions. For instance:

• Peaks in the probability density plot indicate regions where the particle is more likely to be found.

• Troughs suggest lower probabilities.

These representations aid in interpreting quantum phenomena like particle confinement, tunneling, and scattering.

Allowed Electron Energy States

One of the profound implications of wave functions is their ability to predict allowed energy states for electrons in atoms. These states, often called quantized energy levels, emerge from the boundary conditions imposed on the wave function.

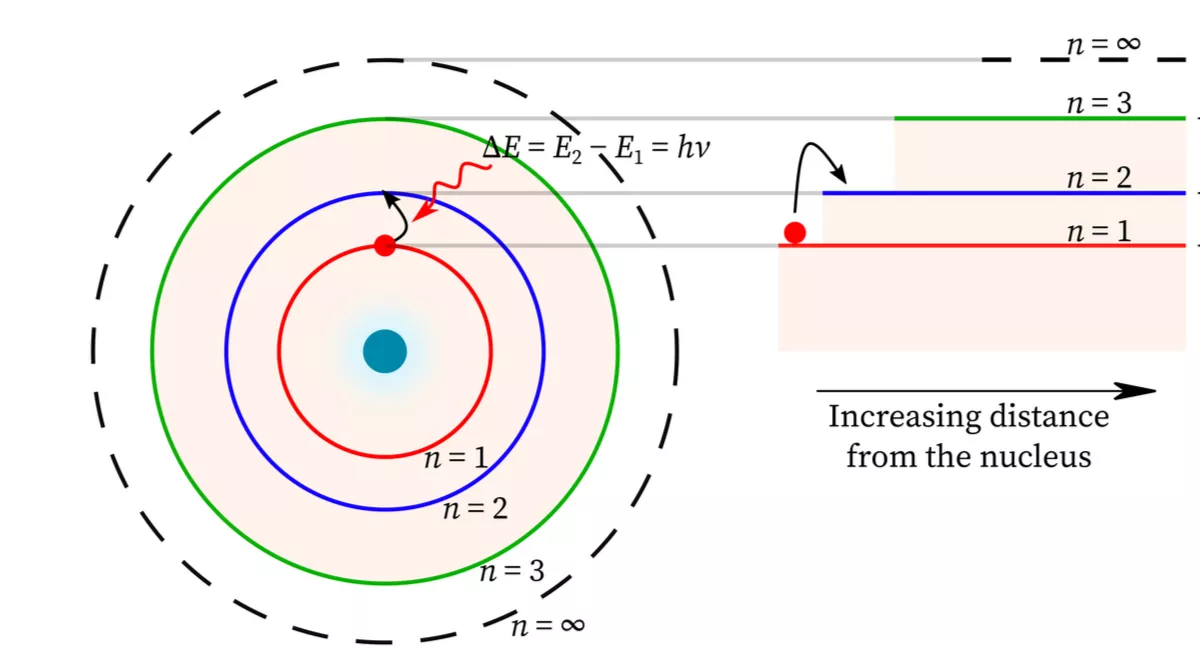
Energy Levels in Atoms:

1. Wave Function and Boundaries:

   • The shape of the wave function and the conditions it must satisfy determine the possible energy levels.

2. Discrete Energy States:

   • Electrons can only occupy specific energy levels within an atom.

3. Spectral Lines:

   • When electrons transition between energy levels, they absorb or emit photons with energy equal to the difference between the levels: ΔE = hf.

Standing Waves in Quantum Mechanics

The energy levels of electrons in atoms are modeled as standing waves. Unlike traveling waves, standing waves oscillate in place, forming fixed patterns with nodes (points of zero amplitude).

Key Aspects of Standing Waves:

1. Stationary Patterns:

   • The wave function’s shape remains constant, with oscillations confined to specific regions.

2. Photon Emission and Absorption:

   • When an electron transitions between standing wave states, it emits or absorbs a photon corresponding to the energy difference.

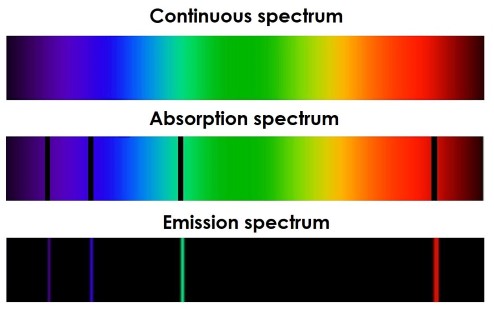
3. Spectral Lines:

   • These transitions lead to discrete spectral lines observed in emission and absorption spectra.

The de Broglie Wavelength

The de Broglie wavelength connects the particle-like and wave-like behaviors of matter. Proposed by Louis de Broglie, it suggests that all particles have an associated wavelength:

λ = h / p,
where:

• λ = Wavelength (m),

• h = Planck’s constant (≈6.63 × 10⁻³⁴ Js),

• p = Momentum (kg·m/s).

Applications of the de Broglie Wavelength:

1. Electron Transitions:

   • The de Broglie wavelength helps model transitions between energy levels as changes in standing wave patterns.

2. Photon Emission:

   • When an electron transitions to a lower energy level, it emits a photon with a wavelength related to the energy difference: λ_photon = hc / ΔE.

3. Quantum Systems:

   • The concept is pivotal in understanding electron diffraction and interference patterns.

Probability in Quantum Processes

Radioactive Decay:

The probabilistic nature of quantum mechanics governs radioactive decay, where the exact time of decay for a single nucleus is unpredictable. However, for a large sample, the half-life provides a statistical measure:

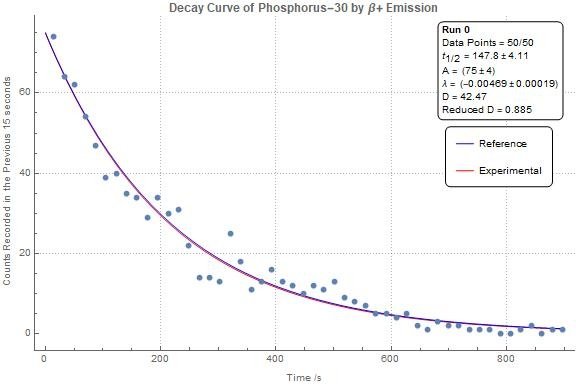
1. Half-Life:

   • Time required for half the nuclei in a sample to decay.

2. Decay Mechanisms:

   • Energy release via emission of particles or radiation.

Examples include:

• Carbon-14: Half-life ≈5,700 years.

• Uranium-238: Half-life ≈4.5 billion years.

Photon Emission and Absorption:

Photon interactions with matter are governed by quantum probabilities:

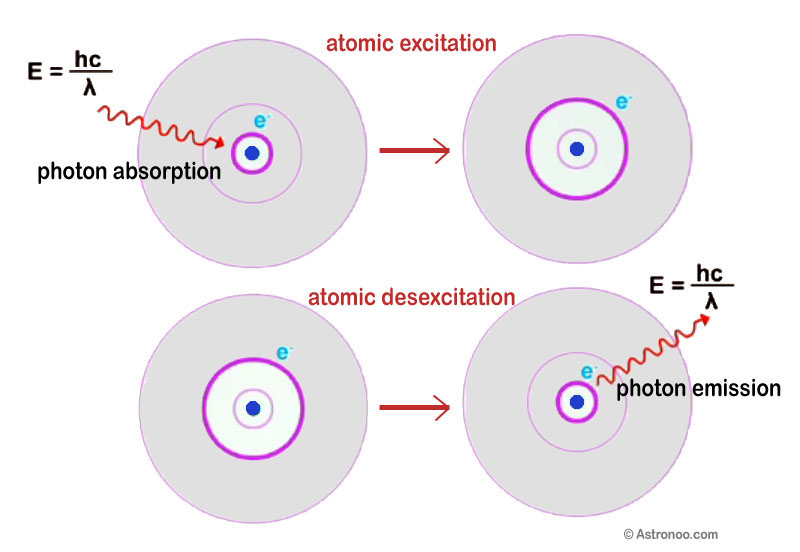
1. Stimulated Absorption:

   • An atom absorbs a photon, moving to a higher energy state if the photon’s energy matches the energy gap.

2. Spontaneous Emission:

   • An excited atom releases a photon and transitions to a lower energy state.

3. Stimulated Emission:

   • A photon interacts with an excited atom, causing it to emit a second photon. This process is key to laser technology.

Practice Problem: Calculating the de Broglie Wavelength

Problem: An electron with a momentum of has what de Broglie wavelength?

Solution:

1. Use the formula: λ = h / p.

2. Substitute values:

3. Calculate:

   • λ = 6.63 × 10⁻³⁴ / 1.0 × 10⁻²´ = 6.63 × 10⁻³´ m.

Answer: The de Broglie wavelength is.