7.5 Properties of Waves and Particles

Properties of Waves and Particles: Understanding Wave-Particle Duality

Introduction

The duality of light—its ability to behave as both a particle and a wave—is one of the most intriguing phenomena in physics. Known as wave-particle duality, this concept extends to fundamental particles like electrons and photons. This article dives deeper into this dual nature and explores its implications in quantum mechanics, relativity, and modern technology.

Wave-Particle Duality

Wave-particle duality is the coexistence of wave-like and particle-like properties in fundamental particles. This principle, central to quantum mechanics, explains phenomena such as diffraction and interference for particles and particle-like behaviors like momentum and energy for waves.

Key Features of Wave-Particle Duality:

1. Wave-like Behavior:

   • Particles such as electrons exhibit wave-like properties, including wavelength and frequency.

   • In the double-slit experiment, particles create interference patterns similar to waves.

2. Particle-like Behavior:

   • Waves such as photons possess momentum and energy, described by the equations:

     • Momentum = h / λ, where h is Planck’s constant and λ is the wavelength.

     • Energy = hf, where f is frequency.

Historical Context:

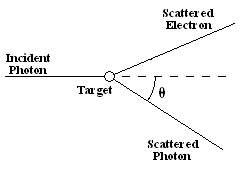
• In the 1920s, physicist Arthur Compton demonstrated the Compton effect, where X-ray photons scattering off electrons obeyed conservation of momentum.

• Louis de Broglie extended this principle to matter, proposing that particles have an associated wavelength: λ = h / p, where (momentum).

De Broglie Wavelength:

The de Broglie wavelength for a particle is given by:

λ = h / mv,

where:

• h = Planck’s constant (≈6.63 × 10⁻³⁴ Js),

• m = mass of the particle (kg),

• v = velocity of the particle (m/s).

For significant wavelengths to be observed, the particle’s mass must be extremely small, making this principle especially relevant at the atomic scale.

Applications of Wave-Particle Duality

Wave-particle duality is essential for understanding quantum mechanics and has far-reaching implications in technology and research.

1. Quantum Mechanics:

   • Describes the behavior of particles at the atomic and subatomic level.

   • Essential for understanding phenomena like electron orbitals and quantum tunneling.

2. Technological Advances:

   • Lasers: Rely on the particle nature of light to produce coherent beams.

   • Transistors: Exploit the quantum behavior of electrons.

3. Experimental Physics:

   • Particle accelerators use the momentum of particles to explore their wave-like properties.

   • Electron microscopy leverages the wave nature of electrons for high-resolution imaging.

Relativistic Mass-Energy Equivalence

Wave-particle duality intersects with relativity through the concept of relativistic mass-energy equivalence. According to Einstein’s equation E=mc², the mass of an object increases as its velocity approaches the speed of light. This relationship has profound implications:

1. Energy-Mass Relationship:

   • Energy is directly proportional to mass and the square of the speed of light.

2. Relativistic Momentum:

   • At high velocities, the momentum of a particle increases, affecting its wavelength.

3. Technological Impact:

   • High-energy physics experiments, such as those at the Large Hadron Collider (LHC), rely on these principles to study fundamental particles.

Wave Phenomena: Interference and Diffraction

Interference and diffraction are hallmark characteristics of waves and are not observed in classical particles. These phenomena provide direct evidence of the wave nature of particles like electrons and photons.

1. Interference:

   • Occurs when two or more waves overlap, creating constructive or destructive interference patterns.

   • Observed in experiments like the double-slit setup.

2. Diffraction:

   • Describes the bending of waves around obstacles or through small openings.

   • Requires the obstacle or opening to be comparable in size to the wavelength of the wave.

Practice Problem: Calculating the De Broglie Wavelength

Problem: Electrons in a diffraction experiment are accelerated through a potential difference of 175 V. Calculate the de Broglie wavelength of these electrons.

Solution:

1. Find the momentum of the electron:

   • Kinetic energy

   • Momentum , where (m = 9.11 × 10⁻³¹ kg.

2. Calculate the wavelength (λ):

   • λ = (9.3 × 10⁻¹¹ m = 0.093 nm.

Practice Problems

1. A very slow proton has its kinetic energy doubled. What happens to the proton’s corresponding de Broglie wavelength?

   • A) The wavelength is decreased by a factor of .

   • B) The wavelength is halved.

   • C) There is no change in the wavelength.

   • D) The wavelength is increased by a factor of .

   • E) The wavelength is doubled.

   Answer: A) The wavelength is decreased by a factor of .

2. Which graph best represents the de Broglie wavelength (λ) of a particle as a function of its linear momentum ?

   • Answer: λ and are inversely proportional, as shown in (p = h / λ).