7.3 Angular Momentum and Torque
Enduring Understanding 4.D
A net torque exerted on a system by other objects or systems will change the angular momentum of the system.
Essential Knowledge
4.D.1: Torque, angular velocity, angular acceleration, and angular momentum are vectors characterized as positive or negative depending on counterclockwise or clockwise rotation.
4.D.2: Angular momentum of a system changes due to interactions with external objects or systems.
4.D.3: Change in angular momentum is given by the product of the average torque and the time interval during which the torque is exerted.
Angular Momentum
Angular momentum is the rotational equivalent of linear momentum.
Formula:
Where:
: Angular momentum (kg⋅m²/s).
: Moment of inertia (kg⋅m²).
: Angular velocity (rad/s).
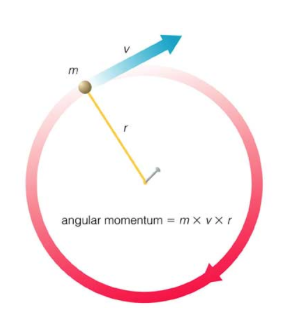
For an object moving in a straight line relative to a fixed point, angular momentum can be calculated as:
Where:
: Mass (kg).
: Linear velocity (m/s).
: Perpendicular distance from the axis of rotation (m).
Key Concept:
Even an object moving linearly can have angular momentum relative to a fixed point. For instance, watching a train pass by from a station involves turning your head, which is an example of angular momentum about a fixed point.
Relationship Between Torque and Angular Momentum
A net torque causes a change in angular momentum. This is analogous to how a net force changes linear momentum.
Formula:
Where:
: Change in angular momentum (kg⋅m²/s).
: Net torque (Nm).
: Time interval (s).
Angular momentum is conserved in a closed system with no external torque.
Example Problem: Maximizing Angular Speed
A disk is slid toward a rod on a pivot, as shown below:
Scenario: A disk of mass with velocity sticks to the rod at a distance from the pivot.
Goal: Maximize the angular speed of the rod-disk system.
Correct Answer:
Hit the rod to the right of its midpoint (point C).
Explanation:
Torque Maximization: Torque depends on distance . Hitting farthest from the pivot maximizes and angular momentum .
Angular Momentum Conservation: Hitting at a greater distance increases the initial angular momentum , leading to a higher angular speed .
Practice Problems
Problem 1:
A spinning disk has mass 0.5 kg, radius 0.2 m, and angular velocity 2 rad/s. What is its angular momentum?
Solution:
Answer: A) 0.02 kg⋅m²/s
Problem 2:
A 0.4 kg ball is attached to a 0.5 m string, rotating at 3 rad/s. What is its angular momentum?
Solution:
Answer: B) 0.12 kg⋅m²/s
Problem 3:
A flywheel (disk) with mass 8 kg, radius 0.3 m, and angular velocity 4 rad/s. What is its angular momentum?
Solution:
Answer: A) 1.44 kg⋅m²/s