7.2 Torque and Angular Acceleration

7.2 Torque and Angular Acceleration

Enduring Understanding 3.F

A force exerted on an object can cause a torque on that object.

Essential Knowledge

• 3.F.1: Only the force component perpendicular to the line connecting the axis of rotation and the point of application results in a torque about that axis.

• 3.F.2: The presence of a net torque along any axis will cause a rigid system or object to change its rotational motion about that axis.

Torque

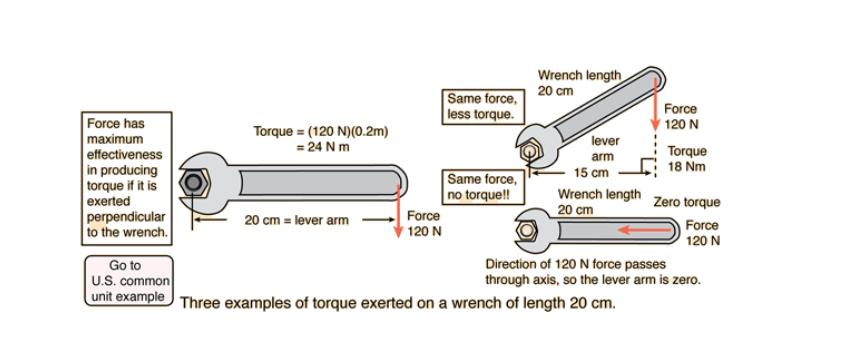
Torque (τ) is the rotational equivalent of force. It determines how a force applied to an object causes it to rotate around a pivot point.

Factors Affecting Torque:

1. Magnitude of Force (τ): The greater the force, the greater the torque.

2. Distance from the Pivot Point (r): Torque increases with the distance from the axis of rotation.

3. Angle (θ) Between Force and Radius Vector: Only the perpendicular component of the force contributes to torque.

Torque Formula:

Where:

• : Torque (Nm).

• : Force (N).

• : Distance from the pivot (m).

• : Angle between and .

Key Concept:

• Torque is maximized when the angle , as .

• Torque is zero when or .

Example: Pushing a door at its edge (far from the hinge) requires less force compared to pushing near the hinge, as the torque increases with distance.

Rotational Equilibrium

An object is in rotational equilibrium when the net torque is zero:

Example:

Problem: A 120 N object sits 3 m from a pivot. What force () must be applied 4 m from the pivot to keep the system balanced?

Solution:

• Counter-clockwise torque (): .

• Clockwise torque (): .

Set torques equal:

Solve for :

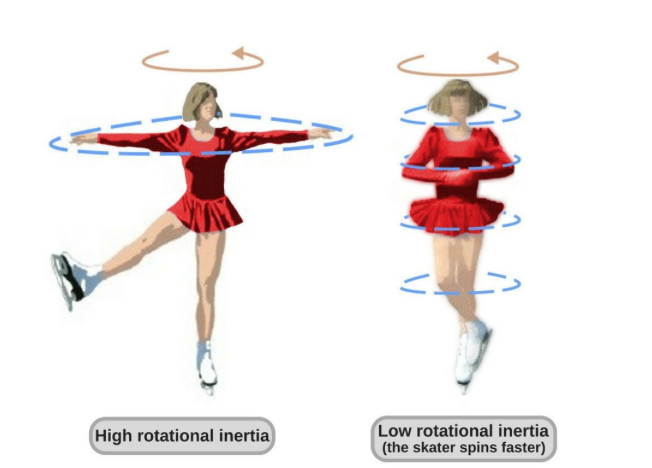
Moment of Inertia

The moment of inertia is the rotational equivalent of mass, describing how difficult it is to rotate an object.

Formula for Point Mass:

Where:

• : Moment of inertia (kg⋅m²).

• : Mass (kg).

• : Distance from the pivot (m).

Key Concept:

• Mass closer to the pivot: Lower moment of inertia, easier to rotate.

• Mass farther from the pivot: Higher moment of inertia, harder to rotate.

Angular Acceleration

Angular acceleration measures the rate of change of angular velocity and is caused by a net torque:

Where:

• : Angular acceleration (rad/s²).

• : Net torque (Nm).

• : Moment of inertia (kg⋅m²).

Newton’s Second Law for Rotation:

Example:

Problem: A rod (length , mass ) pivots at one end. Find the angular acceleration when released from the horizontal position. The moment of inertia of the rod about its end is .

Solution:

• Torque due to weight: .

• Substituting into Newton’s law: