7.1 Rotational Kinematics

7.1 Rotational Kinematics

Learning Targets

Rotational kinematics provides a framework to understand motion in angular terms, using radians to describe position, displacement, velocity, and acceleration. Observers in inertial reference frames can apply these quantities to analyze rotational motion effectively.

The Radian

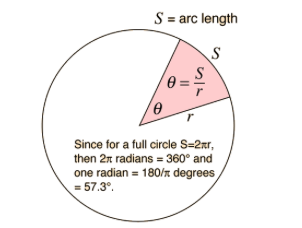
A radian is a natural way to measure angles. To understand it:

• Imagine wrapping the radius of a circle along its circumference. The angle subtended by this arc length is 1 radian.

• Key conversions:

  • π radians = half the circle’s circumference.

  • 2π radians = full circumference.

Basic Rotational Quantities

Rotational motion mirrors linear motion but uses angular counterparts for its quantities:

• Angular Displacement (θ):

  • Change in angular position, measured in radians.

  • Formula:

  • Convert degrees to radians: .

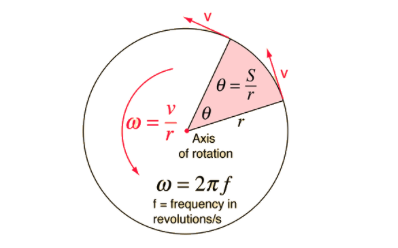
• Angular Velocity (ω):

  • Rate of change of angular displacement, measured in rad/s.

  • Formula:

  • Relation to frequency: .

• Angular Acceleration (α):

  • Rate of change of angular velocity, measured in rad/s².

  • Formula:

Relation to Linear Quantities:

Rotational quantities are linked to linear terms by:

Where is the radius of rotation.

Direction in Rotational Kinematics

Angular displacement, velocity, and acceleration are vector quantities with magnitude and direction:

• Counterclockwise rotation: Positive (+)

• Clockwise rotation: Negative (-)

Tip: A disk spinning clockwise has a negative angular velocity.

Mathematical Representations of Motion

Rotational kinematic equations parallel linear kinematic equations:

Variable Key:

• : Angular displacement (radians).

• : Final and initial angular velocity (rad/s).

• : Angular acceleration (rad/s²).

• : Time (seconds).

Relation to Period:

Where is the period (seconds).