4.2 Work and Mechanical Energy
Key Concepts in Work and Mechanical Energy
Changes in Kinetic Energy
Kinetic energy (KE) represents the energy of motion. It depends on an object’s mass and velocity:
Where:
- : Mass of the object (kg).
- : Velocity of the object (m/s).
Key Points:
- Proportional Relationship: Kinetic energy increases with the square of velocity. Doubling velocity quadruples .
- External Forces: Changes in occur when forces like friction, gravity, or collisions act on an object.
- Formula for Change in Kinetic Energy:
Changes in Total Energy
Interactions with external objects or systems can transfer energy, altering a system’s total energy.
- Work: Transfers energy to or from a system when a force acts over a displacement.
- Mechanical Energy: Sum of and potential energy ().
Forces and Work
The work done on an object depends on:
- The force applied.
- The displacement of the object.
- The angle between the force and displacement vectors.
Work is calculated as:
Where:
- : Force (N).
- : Displacement (m).
- : Angle between force and displacement.
Types of Energy
Kinetic Energy ()
Work can increase , demonstrated by the work-energy principle:
Derivation:
For an object of mass m acted upon by a net force over a displacement :
- Use Newton’s Second Law: .
- Use kinematic equations to relate acceleration and displacement.
- Substitute into the work formula to derive .
Gravitational Potential Energy ()
Work done to change an object’s position relative to a reference point increases its gravitational potential energy:
Where:
- : Mass of the object (kg).
- : Gravitational acceleration ().
- : Height above the reference point (m).
In gravitational systems beyond Earth, can also be calculated using:
Where is the distance between the two masses’ centers.
Elastic Potential Energy ()
Elastic potential energy is stored in deformable objects like springs. For an ideal spring:
Where:
- : Spring constant (N/m).
- : Displacement from equilibrium (m).
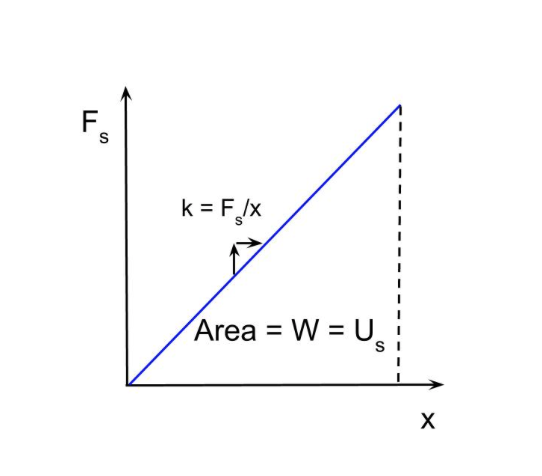
The spring constant can be determined from a plot of force () vs. displacement (), where the area under the curve represents the work done.
Thermal Energy
Thermal energy is a catch-all for non-mechanical energy, such as heat or sound:
- Often arises from friction or collisions.
- In AP Physics 1, no formal equation is required, but it’s a vital part of energy conservation in systems.
Mechanical Energy Conservation
For a closed system with no non-conservative forces:
Key Takeaways on Energy Types
- Kinetic Energy: Motion energy proportional to mass and velocity squared.
- Potential Energy:
- Gravitational: Depends on height and mass.
- Elastic: Stored in springs or deformable materials.
- Thermal Energy: Energy dissipated as heat or sound.
- Mechanical Energy: Sum of and .
Real-World Applications
Roller Coasters:
- Convert at the top of a hill into as the coaster descends.
Springs:
- Elastic potential energy powers systems like trampolines or shock absorbers.
Heat from Friction:
- Tires heating up as they skid due to friction.
Practice Problem
Problem:
A 2 kg object moves at 3 m/s. How much work is required to increase its velocity to 6 m/s?
Solution:
- Calculate initial :
- Calculate final :
- Work done ():