7.4 Conservation of Angular Momentum
Enduring Understanding 5.E
The angular momentum of a system is conserved.
Essential Knowledge
5.E.1: If the net external torque exerted on a system is zero, the angular momentum of the system does not change.
Angular Momentum
Angular momentum is the rotational equivalent of linear momentum and is given by:
Where:
: Angular momentum (kg⋅m²/s).
: Moment of inertia (kg⋅m²).
: Angular velocity (rad/s).
Angular momentum is conserved when there are no net external torques acting on the system. This principle applies to various scenarios, such as spinning ice skaters and planetary motion.
Example: Ice Skater
When a skater pulls their arms in, they reduce their moment of inertia . To conserve angular momentum, their angular velocity increases. Conversely, extending their arms increases , causing to decrease.
Initial State: Large , small .
Final State: Small , large .
This demonstrates how changes in mass distribution affect rotational speed while maintaining constant angular momentum.
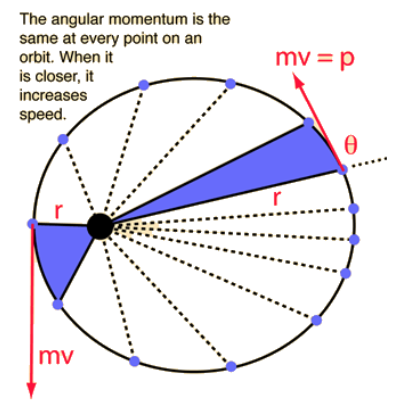
Conservation in Planetary Motion
Angular momentum is conserved in planetary motion because planets move in closed orbits around the Sun. Kepler’s Second Law explains that planets sweep out equal areas in equal time intervals, maintaining constant angular velocity .
Key Points:
Linear Velocity vs Angular Velocity:
Linear velocity changes as a planet approaches or recedes from the Sun.
Angular velocity remains constant to conserve angular momentum.
Gravitational Influence:
Planets move faster when closer to the Sun (greater linear velocity).
Angular momentum is conserved despite these changes.
Example Problem: Rod and Disk System
Scenario: A disk of mass slides towards a rod (length , rotational inertia ) and sticks to it at a distance from the pivot. The system rotates after the collision.
Part (a): Derive Post-Collision Angular Speed
Identify Equations:
Angular momentum of disk before collision: .
Angular momentum of rod-disk system after collision: .
Set Conservation Statement:
Solve for :
Part (b): Disk Bounces Off Rod
Question: Is the post-collision angular speed greater, less than, or equal to the speed when the disk sticks?
Answer: Greater than
Reasoning:
When the disk bounces off, it reverses direction, resulting in a greater change in angular momentum compared to when it sticks.
To conserve total angular momentum, the rod gains additional angular momentum.
Since and is constant, the increase in angular momentum causes an increase in .
Practice Problems
Problem 1:
A disk with mass 0.5 kg, radius 0.2 m, and angular velocity 4 rad/s. Calculate its angular momentum. ()
Solution:
Answer: 0.04 kg⋅m²/s
Problem 2:
A rod (length 1 m, mass 2 kg) rotates about its end. Find the angular momentum if . ()
Solution:
Answer: 2 kg⋅m²/s
Problem 3:
A skater reduces their radius by half while spinning. How does their angular velocity change?
Solution:
Initial angular momentum: .
Final moment of inertia: .
Since is constant: .
Answer: Angular velocity quadruples.







