6.9 Hess’s Law: Mastering Thermochemical Equations with Enthalpy Calculations
Understanding State Functions and Pathway Independence
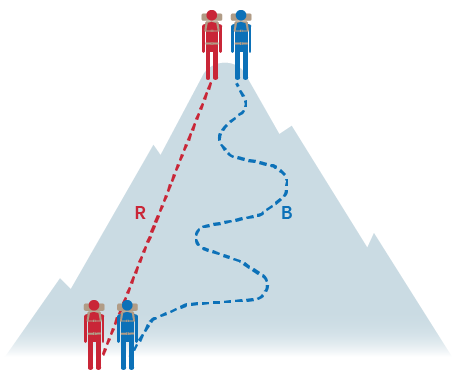
In thermodynamics, it’s crucial to grasp the idea of state functions—properties that depend only on the current state of the system, not the path taken to reach that state. Energy, enthalpy, pressure, volume, and temperature are all state functions, meaning they are pathway independent. Whether you zigzag up a mountain or take a straight path, the change in elevation remains the same! The same holds true for enthalpy changes in reactions.
Hess’s Law Explained
Hess’s Law states that because enthalpy is a state function, the total enthalpy change for a reaction is the same, no matter how many steps the reaction takes. This means that you can determine the enthalpy change of a reaction by breaking it down into multiple steps and using known enthalpy changes for each step.
Key Rules of Hess’s Law:
- Reversing a Reaction: Flipping a reaction reverses the sign of its enthalpy (ΔH).
- Multiplying a Reaction: If you multiply the coefficients of a reaction by a number, you must also multiply ΔH by that same number.
- Adding Reactions: When two or more reactions are added to form a new reaction, their ΔH values are summed.
Example Problem Using Hess’s Law
Given the following thermochemical reactions:
Goal:
Calculate the enthalpy change for the following reaction:
Step-by-Step Solution:
Manipulate Reaction 1:
- Flip it to get C2H2(g) as a product:
- Flip it to get C2H2(g) as a product:
Multiply Reaction 2 by 2:
- To match the two carbon atoms:
- To match the two carbon atoms:
Use Reaction 3 as is:
Adding Reactions:
Combine all modified reactions:
Cancel out spectator species and sum the enthalpies:
Another Example Problem
Reaction:
Given Data:
- ΔHf values:
- CH₄ (g): -74.8 kJ/mol
- CO₂ (g): -393.5 kJ/mol
- H₂O (l): -285.8 kJ/mol
Solution Using Hess’s Law:
Key Takeaways for Using Hess’s Law
- Rearrange Equations: Manipulate given reactions to match your target reaction.
- Flip and Multiply Carefully: Remember to flip signs and multiply enthalpy values accordingly.
- Cancel Spectator Species: Add equations and cancel out intermediates to simplify.
- Add Enthalpies: Sum the modified enthalpy changes to find the total ΔH for the desired reaction.
Practice Problem
Calculate the enthalpy change for the reaction:
Given reactions:
By mastering Hess’s Law, you can calculate enthalpy changes for complex reactions and gain a deeper understanding of thermodynamics!







