6.4 Heat Capacity and Calorimetry
What is Calorimetry?
Calorimetry is the study of heat flow and heat exchange between a system and its surroundings. While the absolute enthalpy (H) of a system cannot be directly measured, changes in enthalpy (ΔH) can be calculated using calorimetry by measuring changes in temperature, which indicate the heat lost or gained during a process.
Types of Calorimeters
Calorimeters are devices used to measure heat flow during a chemical reaction or physical process. Here are some key types:
- Bomb Calorimeter: A sealed container (or “bomb”) is used for combustion reactions. The heat generated raises the temperature of surrounding water, and by measuring the temperature increase, the heat of reaction can be determined.
- Constant-Pressure Calorimeter: Measures heat changes at constant pressure, typically used for reactions in solutions, as the heat transferred equals ΔH.
- Coffee-Cup Calorimeter: A simple version of a constant-pressure calorimeter. This setup often uses a styrofoam cup, a thermometer, and a stirrer to insulate and measure temperature changes accurately.
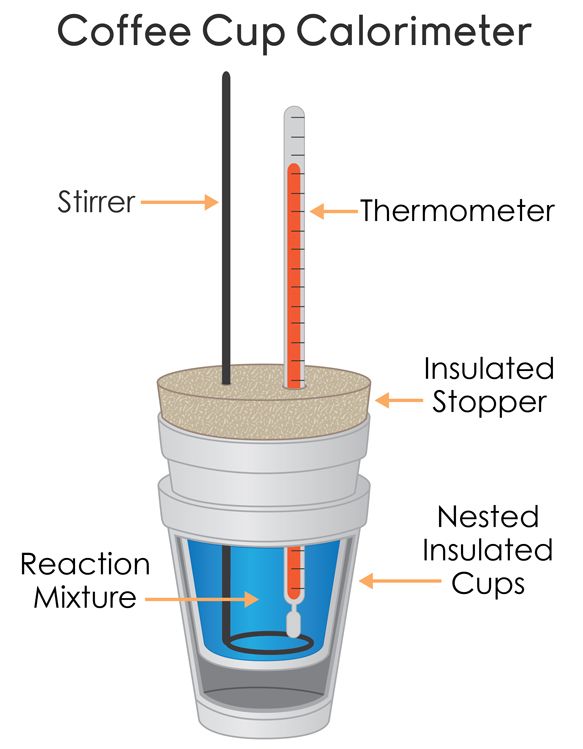
Coffee-Cup Calorimetry in Detail
The coffee-cup calorimeter has several components:
- Thermometer: Measures temperature change.
- Reaction Mixture: The chemical reaction takes place here.
- Stirrer: Ensures uniform temperature throughout the mixture.
- Insulated Container: Reduces heat exchange with surroundings.
- Heat-Proof Lid: Helps further insulate the system.
The goal of this calorimeter is to minimize heat loss, making it ideal for measuring heat changes during chemical reactions.
Quantifying Energy with Calorimetry
The First Law of Thermodynamics
The First Law of Thermodynamics states that energy cannot be created or destroyed, only transferred or converted. This means that the energy within a closed calorimeter remains constant. In calorimetry, this law ensures that all energy changes within the system can be measured accurately.
Measuring Heat Transferred: The q = mcΔT Formula
To quantify the energy change during a reaction, use the equation:
- q = heat (Joules, J)
- m = mass (grams, g)
- C = specific heat capacity (J/g°C)
- ΔT = change in temperature (final – initial, °C or K)
Note: The temperature change (ΔT) remains the same whether expressed in Celsius or Kelvin. Specific heat is the amount of heat required to raise the temperature of 1 gram of a substance by 1°C.
Real-World Examples of Specific Heat
1. Water (H₂O)
Water has a high specific heat of 4.184 J/g°C, meaning it takes a lot of energy to change its temperature. This is why boiling water takes time; it needs to absorb significant energy.
2. Sand
Sand has a lower specific heat of around 0.840 J/g°C, making it heat up and cool down much faster than water. This is why sand at the beach becomes hot quickly under the sun compared to water.
Example Problem 1: Heat Transfer in Water
Problem: An insulated cup contains 255.0 grams of water, and the temperature changes from 25.2°C to 90.5°C. Calculate the heat released by the system.
Given: Specific heat of water = 4.184 J/g°C.
Solution:
Misconception: q vs. ΔH
While q represents the magnitude of heat transfer, ΔH can be positive or negative depending on whether heat is absorbed or released. q is always considered a positive magnitude for energy change.
Example Problem 2: Finding Specific Heat of Copper
Scenario:
- Mass of Copper = 50.00g
- Initial Temperature of Copper = 100.0°C
- Mass of Water = 100.00g
- Initial Temperature of Water = 20.0°C
- Final Temperature of System (Copper and Water) = 23.6°C
- Specific heat capacity of water = 4.18 J/g°C
- Find the specific heat of copper.
Solution:
Calculate ΔT for both substances:
- Copper: |23.6°C – 100.0°C| = 76.4°C
- Water: 23.6°C – 20.0°C = 3.6°C
Assume heat lost by copper = heat gained by water:
Solving for C:
Another Formula for Heat Exchange
For problems involving heat exchange between two substances, use:







