Unit 7 Overview: Torque and Rotational Motion
Introduction
Up until this point, we’ve focused on linear motion concepts such as forces, velocities, and displacements. However, much of the motion in the world involves rotation around a fixed axis, such as wheels, merry-go-rounds, and record players.

This unit builds upon the concepts from Units 1-6 and applies them to rotating objects. Rotational motion topics account for approximately 10-16% of AP exam questions and require around 12-17 class periods to cover.
Applicable Big Ideas
Big Idea #3: Force Interactions — Describing the interactions of objects using forces.
Big Idea #4: Change — Understanding changes in systems due to interactions.
Big Idea #5: Conservation — Explaining changes using conservation laws.
Key Concepts
Angular Displacement (θ)
Angular Velocity (ω)
Angular Acceleration (α)
Period (T)
Torque (τ)
Moment of Inertia (I)
Rotational Kinetic Energy (Krot)
Angular Momentum (L)
7.1 Rotational Kinematics
Rotational kinematics describes the motion of rotating objects using rotational equivalents of linear motion.
Key Terms and Relationships:
Angular Displacement (Δθ): Change in angular position (measured in radians).
where is the linear displacement and is the radius.
Angular Velocity (ω): Rate of change of angular displacement.
where is the linear velocity.
Angular Acceleration (α): Rate of change of angular velocity.
where is the linear acceleration.
Equations of Rotational Motion:
Tip: Counterclockwise rotation is positive; clockwise rotation is negative.
7.2 Torque and Angular Acceleration
Torque (τ): A measure of the twisting force causing rotation.
Where:
: Lever arm distance.
: Force applied.
: Angle between and .
Newton’s Second Law for Rotation:
Where:
: Moment of inertia (“rotational mass”), given by .
: Shape constant.
7.3 Angular Momentum and Torque
Angular Momentum (L): A measure of rotational motion.
Equations for Angular Momentum:
Change in Angular Momentum:
Angular Momentum for Linear Motion:
7.4 Conservation of Angular Momentum
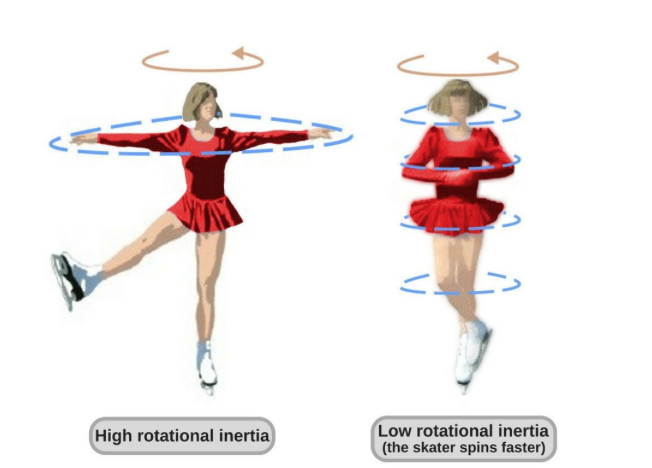
The total angular momentum of a closed system remains constant if no external torque acts on it.
Example: A figure skater pulling in their arms reduces their moment of inertia , causing an increase in angular velocity , while remains constant.