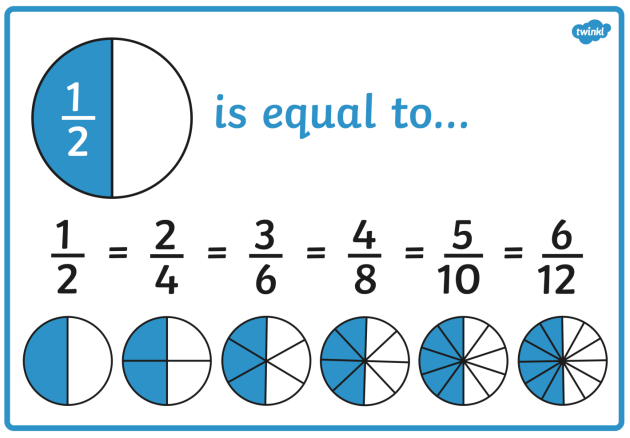What Is Equivalent?

“What Is Equivalent?” Everything You Need to Know

The concept of equivalence is woven into every aspect of our lives—from mathematics and science to everyday decision-making and comparisons in business. But what is equivalent exactly, and why is understanding equivalence so important? In this comprehensive guide, we’ll break down the definition of equivalence, explore its historical evolution and contextual background, and delve into its various applications across multiple disciplines. Whether you’re a student, a professional, or just a curious mind, this article will provide you with a deep and engaging understanding of what is equivalent and how this idea helps us compare, measure, and balance elements in our world.

Introduction: The Ubiquity of Equivalence

Imagine trying to compare two things without a common basis—a challenge in math, science, or even in everyday choices. Equivalence is the principle that allows us to say, “These two things are the same in value, function, or meaning.” For instance, consider currency exchange: determining that 1 U.S. dollar is equivalent to a certain amount of euros enables global trade and travel. Similarly, in chemistry, equivalent weights allow scientists to compare substances on a common scale.

Have you ever wondered how such a seemingly simple idea—equivalence—can have such far-reaching implications? In this post, we will cover:

• A Clear Definition: We’ll start by defining what equivalence means in various contexts and pinpoint its essential characteristics.
• Historical and Contextual Background: We’ll trace the evolution of the concept of equivalence from its philosophical and mathematical roots to its modern applications.
• In-Depth Exploration: We’ll break down the different facets of equivalence in mathematics, science, economics, and everyday reasoning.
• Real-World Examples and Case Studies: Learn how equivalence plays a critical role in currency conversion, chemical reactions, legal standards, and more.
• Importance, Applications, and Benefits: Understand why grasping equivalence is crucial for making informed decisions and optimizing processes in multiple domains.
• Common Misconceptions and FAQs: We’ll clear up myths and answer your frequently asked questions about equivalence.
• Modern Relevance and Current Trends: Discover how recent developments in technology and research continue to shape our understanding of equivalence.

By the end of this article, you’ll have a comprehensive understanding of what is equivalent, why it matters, and how you can apply this principle in various areas of life. Let’s embark on a journey to uncover the power of equivalence!

What Is Equivalent? A Straightforward Definition

Equivalence refers to a state of being equal in value, function, meaning, or effect. In its most basic form, it means that two or more items, quantities, or expressions are considered the same according to a specific set of criteria. However, the idea of equivalence takes on different nuances depending on the context:

• Mathematics: Two mathematical expressions are equivalent if they yield the same value for all variable inputs. For example, the fractions 1/2 and 2/4 are equivalent because they represent the same numerical value.
• Chemistry: In chemistry, equivalent weight is a concept used to compare the reactive capacity of different substances. Two substances are equivalent if they react in the same proportion in a given reaction.
• Logic and Language: In everyday language and logic, statements are equivalent if they convey the same meaning or truth value.
• Economics: Equivalence is used in economic analysis to compare different quantities or values, such as currency exchange rates or the equivalence of different units of measurement in trade.

Essential Characteristics of Equivalence

• Equality in Value: At its core, equivalence means that two entities, despite perhaps appearing different, share the same value or effect when measured against a common standard.
• Substitutability: If two things are equivalent, one can be substituted for the other without affecting the outcome.
• Context-Dependent: The criteria for determining equivalence can vary widely depending on the field of study or the situation at hand.
• Consistency: Equivalence should hold consistently across the range of conditions for which it is defined. In mathematics, for instance, equivalence is rigorously defined through properties like reflexivity, symmetry, and transitivity.

Understanding what is equivalent in these terms provides a solid foundation for exploring its various applications and implications across multiple domains.

Historical and Contextual Background

Philosophical Roots of Equivalence

The idea of equivalence can be traced back to ancient philosophical inquiries. Early thinkers pondered questions of sameness and difference, laying the groundwork for the modern concept of equivalence.

• Ancient Greek Philosophy:
  Philosophers such as Plato and Aristotle explored the nature of similarity and difference. Aristotle, for example, examined how objects could be said to be “the same” in some respects while different in others—a precursor to later formal definitions of equivalence.
• The Development of Logic:
  With the emergence of formal logic in the Middle Ages and the Renaissance, thinkers began to use equivalence in the construction of arguments and the analysis of language. The concept of logical equivalence—where two statements are considered equivalent if they have the same truth value—became a cornerstone of deductive reasoning.

Mathematical Formalization of Equivalence

The rigorous mathematical treatment of equivalence began in earnest during the development of abstract algebra and set theory in the 19th and 20th centuries.

• Equivalence Relations:
  Mathematicians introduced the concept of equivalence relations, which are defined by three properties: reflexivity, symmetry, and transitivity. These properties help formalize the idea that certain elements within a set can be grouped together as equivalent.
• Congruence and Equality:
  In geometry and number theory, concepts like congruence (in geometry) and modular arithmetic (in number theory) illustrate how different expressions or numbers can be equivalent under specific operations or transformations.

Key Historical Milestones

• Development of the Fraction Concept:
  The understanding that 1/2 is equivalent to 2/4 was a breakthrough in arithmetic, allowing early mathematicians to develop the concept of ratios and proportions.
• Advances in Chemical Stoichiometry:
  In the 18th century, scientists like Antoine Lavoisier laid the groundwork for chemical stoichiometry, which relies on the idea that substances can be compared based on their equivalent reactive capacities.
• Economic Theory:
  In economics, the development of standardized measurement systems (such as currency and weight) has allowed for the concept of equivalence to be applied to market transactions, enabling fair trade and economic analysis.

These historical insights provide context for understanding what is equivalent and highlight how this concept has evolved to become a fundamental tool in various disciplines.

In-Depth Exploration: The Many Facets of Equivalence

To fully appreciate what is equivalent, it is essential to explore its diverse applications and manifestations across different fields. Below, we break down key points, attributes, and categories related to equivalence.

1. Equivalence in Mathematics

Mathematics provides the most rigorous and widely applicable framework for understanding equivalence. Here, we explore several aspects of mathematical equivalence.

a. Equivalence Relations and Sets

• Definition:
  An equivalence relation on a set is a binary relation that is reflexive, symmetric, and transitive. This allows us to partition a set into equivalence classes.
• Examples:
  • Congruence in Geometry: Two shapes are equivalent if they are congruent, meaning one can be transformed into the other through rotations, translations, or reflections.
  • Modular Arithmetic: In number theory, numbers are considered equivalent (or congruent modulo a given number) if they leave the same remainder when divided by that number.

b. Algebraic Equivalence

• Simplification of Expressions:
  In algebra, different expressions can be equivalent if they simplify to the same form. For example, the expressions $\frac{2x}{4}$ and $\frac{x}{2}$ are equivalent.
• Properties:
  Algebraic equivalence relies on the fundamental properties of operations such as the distributive, associative, and commutative properties.

c. Functional Equivalence

• Definition:
  Two functions are equivalent if they yield the same output for all inputs in their domain. This concept is crucial in areas such as calculus and analysis.
• Applications:
  Functional equivalence is used in solving equations, optimizing functions, and even in computer science for algorithm design.

2. Equivalence in Chemistry

In chemistry, the idea of equivalence is central to understanding reactions and stoichiometry.

a. Equivalent Weight

• Definition:
  Equivalent weight is the mass of a substance that reacts with or supplies one mole of hydrogen ions (H$^+$) or electrons in a reaction.
• Significance:
  This concept allows chemists to compare the reactive capacities of different substances, which is essential for balancing chemical equations and designing reactions.
• Example:
  In acid-base reactions, the equivalent weight of an acid is the mass required to furnish one mole of H$^+$ ions.

b. Stoichiometric Equivalence

• Definition:
  In a chemical reaction, stoichiometric equivalence means that the amounts of reactants and products are in the proper ratio as dictated by the balanced equation.
• Applications:
  This is used to calculate yields, determine limiting reactants, and design industrial processes to ensure optimal production.

3. Equivalence in Economics

Economic theory also relies heavily on the concept of equivalence, particularly in the context of value and trade.

a. Currency Equivalence

• Definition:
  Currency equivalence refers to the concept that different currencies can be exchanged based on a set rate, allowing for comparisons of value across borders.
• Real-World Example:
  When traveling internationally, you convert your home currency into the local currency based on the current exchange rate, which establishes equivalence between the two.

b. Utility and Value Equivalence

• Definition:
  In economics, utility equivalence refers to the idea that different goods or services can provide the same level of satisfaction or utility to a consumer.
• Applications:
  This concept is foundational in consumer choice theory and market equilibrium analysis, helping to explain how resources are allocated based on relative value.

4. Equivalence in Everyday Reasoning

Outside of formal disciplines, the idea of equivalence is used in everyday reasoning and decision-making.

a. Comparative Statements

• Everyday Use:
  People often make statements of equivalence without realizing it. For example, saying “a dollar is equivalent to a certain amount of goods” is a common way to compare purchasing power.
• Decision Making:
  Equivalence helps individuals assess alternatives, such as determining which product offers the best value for money based on price and quality comparisons.

b. Legal and Social Equivalence

• In Law:
  Legal systems often use equivalence to ensure fairness. For instance, in sentencing, the concept of equivalent punishment aims to balance the severity of different crimes.
• Social Contexts:
  Social equivalence can refer to the idea that individuals should be treated equally under the law or in social policies, reinforcing the principle of fairness.

Real-World Examples and Case Studies

Understanding what is equivalent becomes clearer when we see it applied in real-world contexts. Below are several examples and case studies across different fields.

a. Mathematics and Education

• Textbook Examples:
  In mathematics classes, students learn that fractions like $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent. This fundamental concept is essential for solving problems in algebra, calculus, and beyond.
• Practical Applications:
  When comparing measurements in different units (e.g., converting inches to centimeters), equivalence allows for accurate calculations and comparisons.

b. Chemical Reactions and Industrial Processes

• Industrial Synthesis:
  Chemical engineers use the concept of equivalent weight to scale up reactions. For example, ensuring that reactants are mixed in the correct proportions based on their equivalent weights maximizes yield and efficiency in large-scale production.
• Pharmaceutical Manufacturing:
  Accurate dosage in medication relies on stoichiometric equivalence, ensuring that active ingredients react in predictable, balanced ways to produce the desired therapeutic effect.

c. Economic Transactions

• Foreign Exchange Markets:
  In global finance, the concept of equivalence is critical when converting currencies. Exchange rates determine the equivalence of one currency to another, which in turn affects international trade, investment, and travel.
• Consumer Decision-Making:
  Shoppers often compare products on an equivalent basis—for instance, evaluating which of two products offers more quantity or better quality per dollar spent.

d. Everyday Comparisons

• Energy Efficiency Ratings:
  When shopping for appliances, consumers compare energy ratings to determine equivalence in efficiency, even if the models differ in size or features.
• Nutritional Equivalence:
  In food labeling, products may be compared based on caloric or nutritional equivalence, helping consumers make healthier choices.

Importance, Applications, and Benefits of Equivalence

Understanding what is equivalent is essential because it allows us to make meaningful comparisons, optimize processes, and ensure fairness across a wide range of fields. Here are some key benefits and applications:

a. Enhanced Decision-Making

• Informed Comparisons:
  By understanding equivalence, individuals and businesses can make better decisions. For example, comparing the cost-effectiveness of different investments or products relies on establishing equivalence between their values.
• Optimized Processes:
  In industrial and chemical processes, ensuring that components are mixed in equivalent proportions leads to higher yields and more efficient reactions.

b. Standardization and Fairness

• Legal and Social Systems:
  Equivalence ensures that similar cases or conditions are treated equally, which is vital for maintaining fairness in legal judgments and social policies.
• Economic Stability:
  Currency equivalence and standard measures of value help maintain economic stability by facilitating trade and investment across diverse markets.

c. Educational Value

• Foundational Concept:
  Equivalence is a cornerstone of education in mathematics, science, and economics. Mastering this concept is essential for understanding more complex theories and applications.
• Critical Thinking:
  Learning about equivalence encourages analytical thinking and the ability to assess relationships between seemingly different entities.

d. Innovation and Research

• Advancing Technology:
  In fields such as materials science and nanotechnology, establishing equivalence between different formulations can lead to breakthroughs in product design and functionality.
• Interdisciplinary Applications:
  The concept of equivalence bridges disciplines, allowing insights from one field to inform and enhance understanding in another.

Addressing Common Misconceptions and FAQs

Despite its importance, several misconceptions about equivalence persist. Here, we address some of the most common misunderstandings and answer frequently asked questions.

Common Misconceptions

• Misconception 1: Equivalence Means Identical.
  Reality: While equivalence implies equality in value or function, it does not necessarily mean that two things are identical in every aspect. They may be different in appearance or form yet equivalent in terms of their effect or outcome.

• Misconception 2: Equivalence Is Only a Mathematical Concept.
  Reality: Although equivalence is rigorously defined in mathematics, the principle applies broadly across chemistry, economics, biology, law, and everyday decision-making.

• Misconception 3: Establishing Equivalence Is Always Straightforward.
  Reality: Determining equivalence often requires context-specific criteria and careful analysis, especially when comparing complex systems or diverse units of measurement.

Frequently Asked Questions

• Q: What is the simplest definition of equivalence?
  A: Equivalence means that two or more items have the same value, function, or effect when compared under a specific set of criteria.

• Q: How do mathematicians use the concept of equivalence?
  A: Mathematicians define equivalence relations that group objects into classes where every member of a class is equivalent to the others. This is essential for simplifying problems and proving theorems.

• Q: Can equivalence be applied to qualitative comparisons?
  A: Yes, equivalence is not limited to quantitative measures; it can also apply to qualitative assessments, such as determining that two legal arguments or literary themes are equivalent in impact.

• Q: How does equivalence impact everyday life?
  A: Equivalence helps us compare products, measure nutritional values, convert currencies, and assess the fairness of policies, among other applications.

• Q: What role does equivalence play in scientific research?
  A: In science, equivalence is crucial for standardizing measurements, comparing experimental results, and establishing consistent methods for data analysis and interpretation.

Modern Relevance and Current Trends

The concept of equivalence remains as relevant today as ever, with ongoing research and technological advances continually enhancing our understanding and applications of this principle.

a. Technological Innovations and Standardization

• Digital Conversions and Data Standardization:
  In our digital age, establishing equivalence is essential for data integration across various platforms and systems. Standards for data exchange ensure that information from different sources is equivalent and interoperable.

• Advanced Manufacturing:
  In industrial settings, technologies such as 3D printing and automation rely on precise measurements and equivalence principles to ensure consistency and quality across products.

b. Economic and Social Applications

• Global Trade:
  Equivalence in currency exchange and international trade is critical for economic stability. Modern financial systems use complex algorithms to ensure that different currencies remain equivalent in value.

• Policy and Regulation:
  In governance, establishing equivalence in legal standards and social policies helps create fair and balanced systems, ensuring that similar cases are treated equally regardless of context.

c. Educational and Interdisciplinary Research

• Innovative Teaching Tools:
  Interactive simulations and digital platforms are helping students visualize and understand equivalence in various contexts—from solving algebraic equations to balancing chemical reactions.

• Interdisciplinary Studies:
  Researchers are increasingly applying the concept of equivalence to bridge gaps between disciplines. For example, principles from physics and mathematics are being used to develop more robust economic models and vice versa.

d. Environmental and Sustainability Initiatives

• Resource Equivalence:
  Equivalence is critical in environmental science for comparing the impacts of different pollutants or assessing the sustainability of various energy sources. Life cycle assessments often rely on establishing equivalence between different environmental impacts.

• Green Technologies:
  In the push for sustainable development, technologies that convert waste into energy or that standardize renewable energy outputs rely on equivalence principles to ensure efficiency and viability.

These modern trends illustrate that what is equivalent is a living, evolving concept that continues to drive innovation and progress across multiple domains.

Conclusion: Embracing the Principle of Equivalence

In summary, understanding what is equivalent is essential for making informed decisions, optimizing processes, and ensuring fairness in both scientific inquiry and everyday life. Equivalence is a versatile concept that allows us to compare, balance, and standardize different entities—whether they are numbers, chemical substances, economic values, or even abstract ideas.

Key Takeaways

• Definition and Characteristics:
  Equivalence means that two or more items have the same value, function, or effect when evaluated under a common set of criteria. It involves equality, substitutability, and context-specific standards.

• Historical Evolution:
  The concept of equivalence has evolved from ancient philosophical ideas and early mathematical concepts to sophisticated, formalized systems used in modern science, economics, and beyond.

• Practical Applications:
  Equivalence is fundamental in fields ranging from mathematics and chemistry to economics and everyday reasoning. It enables us to make accurate comparisons, standardize measurements, and optimize resource allocation.

• Modern Relevance:
  Advances in technology, interdisciplinary research, and global standardization efforts continue to underscore the importance of equivalence in our increasingly connected world.

Call to Action

Now that you have a comprehensive understanding of what is equivalent, here are some steps to deepen your engagement:

• Explore Further:
  Check out reputable resources such as Khan Academy, MIT OpenCourseWare, and academic journals that delve into topics like equivalence relations, stoichiometry, and economic modeling.
• Experiment and Learn:
  Whether you’re solving math problems, balancing chemical equations, or comparing financial options, apply the principle of equivalence to enhance your problem-solving skills.
• Join the Conversation:
  Share your thoughts, questions, and experiences with equivalence in the comments below or on social media. Engage with communities of learners and experts to broaden your understanding.
• Apply Your Knowledge:
  Use your insights on equivalence in your professional or academic work, whether it’s through research, teaching, or everyday decision-making.

We invite you to share this post with colleagues, students, and anyone curious about what is equivalent. Your feedback is invaluable—let’s continue the discussion and learn together about the power of balance and equivalence in our world.

Final Thoughts

Equivalence is more than just a theoretical concept—it’s a fundamental principle that underpins many aspects of our lives. By understanding what is equivalent, you can unlock new insights into how systems work, how to compare disparate entities, and how to achieve balance in both practical and abstract contexts. Whether you’re navigating complex mathematical problems, optimizing chemical reactions, or making everyday decisions, the concept of equivalence provides a powerful tool for achieving clarity and precision.

Thank you for joining us on this in-depth exploration of equivalence. We hope this guide has enriched your understanding and sparked your curiosity to explore further. Happy learning, and here’s to discovering the power of equivalence in every facet of life!