9.8 Cell Potential and Free Energy: A Comprehensive Guide

Understanding Cell Potential and Electromotive Force

In this section, we delve into cell potential and its critical role in predicting the spontaneity of redox reactions. By examining electromotive force (EMF), you can determine how electrons move within a galvanic cell, thus predicting thermodynamic favorability.

What is Cell Potential?

Cell potential, measured in volts (V), represents the electromotive force generated by redox reactions within an electrochemical cell. This potential is created when electrons move from the anode (where oxidation occurs) to the cathode (where reduction occurs) through a wire, generating a measurable voltage. The magnitude of this force indicates the spontaneity of the redox reaction.

For standard conditions (1 M concentrations, 298 K, and 1 atm pressure), the standard cell potential (E°cell) can be calculated using: $E°_{\text{cell}} = E_{\text{cathode}} – E_{\text{anode}}$

Example Calculation: Consider the following reaction: $2 \text{AgBr} + 2 \text{Hg} \rightarrow 2 \text{Ag} + \text{Hg}_2\text{Br}_2$

Given reduction potentials:

• $\text{Hg}_2\text{Br}_2 + 2e^- \rightarrow 2\text{Hg} + 2\text{Br}^- \quad (E = +0.140 \text{ V})$
  
• $2\text{AgBr} + 2e^- \rightarrow 2\text{Ag} + 2\text{Br}^- \quad (E = +0.071 \text{ V})$
  

Here, AgBr is reduced (cathode), while Hg is oxidized (anode): $E°_{\text{cell}} = 0.071 \text{ V} – 0.140 \text{ V} = -0.069 \text{ V}$

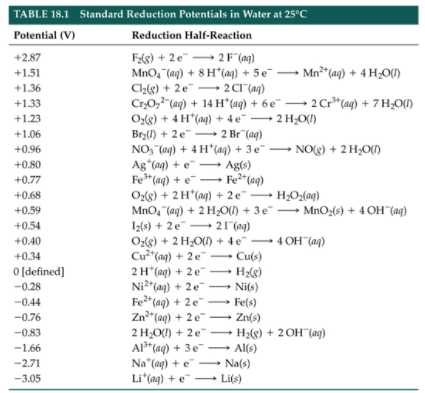
Calculating Cell Potential Using Standard Reduction Potentials

A table of standard reduction potentials provides a list of reactions with their corresponding potentials. When calculating cell potential:

• Identify the anode (oxidation) and cathode (reduction) half-reactions.
• Apply: $E°_{\text{cell}} = E_{\text{cathode}} – E_{\text{anode}}$

Spontaneity and Thermodynamic Favorability 🔋

The sign of E°cell is directly related to spontaneity:

• If E°cell > 0, the reaction is spontaneous (thermodynamically favored).
• If E°cell < 0, the reaction is nonspontaneous (thermodynamically unfavorable).

Relationship with Gibbs Free Energy (ΔG°):

$$\Delta G° = -nFE°_{\text{cell}}$$

• ΔG°: Standard Gibbs Free Energy change (Joules or kJ)
• n: Number of moles of electrons transferred
• F: Faraday’s constant ($96,485 \text{ C/mol e}^-$)

Example Problem: Given a galvanic cell with:

• E°cell = 1.02 V
• n = 1 mole of electrons

Calculate ΔG°:

$$\Delta G° = -nFE°_{\text{cell}} = -1(96,485)(1.02) = -98,414.7 \text{ J} \approx -98.414 \text{ kJ}$$

Calculate the equilibrium constant (K) using:

$$K = e^{-\Delta G°/RT}$$

Where $R = 8.314 \text{ J/mol·K}$ and $T = 298 \text{ K}$:

$$K = e^{98,414.7/(8.314 \times 298)} \approx 1.78 \times 10^{17}$$

Key Takeaways

• Cell potential measures the voltage of redox reactions, indicating spontaneity.
• Use standard reduction potentials to calculate E°cell.
• The relationship between E°cell and ΔG° helps determine whether a reaction is thermodynamically favored.