9.3 Gibbs Free Energy and Thermodynamic Favorability


Table of Contents
Toggle9.3 Gibbs Free Energy and Thermodynamic Favorability in Chemistry
Understanding thermodynamic favorability is key to predicting whether a chemical reaction will proceed on its own (spontaneous) or require external input (nonspontaneous). This essential concept combines the interplay of enthalpy (ΔH°) and entropy (ΔS°), culminating in the calculation of Gibbs Free Energy (ΔG°).
Explaining Thermodynamic Favorability
A spontaneous process occurs without any outside intervention, while a nonspontaneous reaction requires energy input. Spontaneity indicates thermodynamic favorability, with spontaneous reactions being termed thermodynamically favorable and nonspontaneous ones unfavorable. This concept is closely tied to the equilibrium constant (K) and helps determine if a reaction favors the formation of products or reactants.
The Role of Enthalpy (ΔH°) and Entropy (ΔS°)
Enthalpy Change (ΔH°)
Enthalpy measures heat transfer between a system and its surroundings during a reaction:- ΔH° < 0 (Negative): Exothermic reaction (releases heat).
- ΔH° > 0 (Positive): Endothermic reaction (absorbs heat).
Entropy Change (ΔS°)
Entropy represents the disorder or randomness within a system:- ΔS° > 0 (Positive): Increased disorder (more chaotic system).
- ΔS° < 0 (Negative): Decreased disorder (more ordered system).
Combining these measures helps us predict reaction spontaneity using a new term: Gibbs Free Energy.
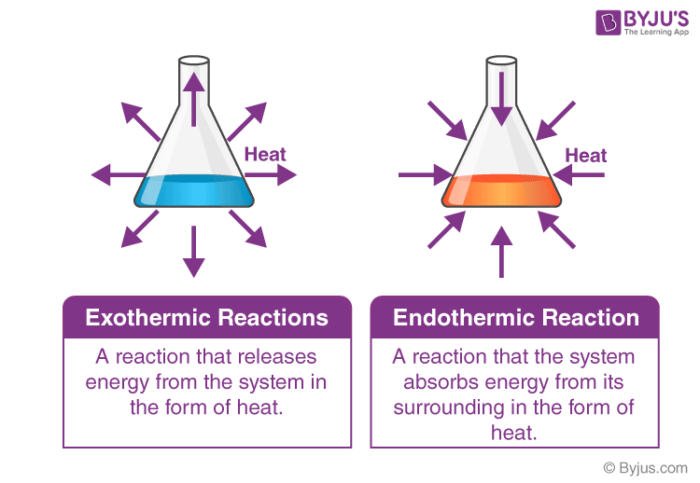

Image Courtesy of Byju’s
Introducing Gibbs Free Energy (ΔG°)
Gibbs Free Energy (ΔG°) quantifies the energy available to do work in a reaction and determines spontaneity:
- ΔG° = ΔH° – TΔS°
Here, T is temperature (in Kelvin), ΔH° is enthalpy change, and ΔS° is entropy change.
Interpreting ΔG°:
- ΔG° < 0 (Negative): Reaction is spontaneous and thermodynamically favorable (exergonic).
- ΔG° > 0 (Positive): Reaction is nonspontaneous and thermodynamically unfavorable (endergonic).
Practice Problem
Given Reaction: 2H₂ + N₂ ⇌ N₂H₄
Conditions: ΔH° = 50.6 kJ/mol, ΔS° = -0.332 kJ/(mol•K), Temperature = 25°C
Solution:
- Convert temperature to Kelvin: T = 25 + 273 = 298 K
- Apply the Gibbs Free Energy formula:
ΔG° = ΔH° – TΔS°
ΔG° = (50.6 kJ/mol) – 298 K * (-0.332 kJ/(mol•K))
ΔG° = 50.6 kJ/mol + 98.936 kJ/mol = 149.5 kJ/mol
Since ΔG° > 0, the reaction is nonspontaneous.
Conditions for Reaction Spontaneity
The sign of ΔG° depends on ΔH°, ΔS°, and temperature:
- Both ΔH° < 0 (Exothermic) and ΔS° > 0 (Increased Disorder)
- Always Spontaneous (ΔG° < 0).
- Both ΔH° > 0 (Endothermic) and ΔS° < 0 (Decreased Disorder)
- Always Nonspontaneous (ΔG° > 0).
- ΔH° < 0 and ΔS° < 0
- Spontaneous at Low Temperatures (ΔH° dominates).
- ΔH° > 0 and ΔS° > 0
- Spontaneous at High Temperatures (TΔS° dominates).
Key Insight: Temperature plays a crucial role in determining spontaneity when ΔH° and ΔS° have opposite signs.
Entropy-Driven vs. Enthalpy-Driven Reactions
Entropy-Driven Reactions
Reactions where spontaneity arises from increased disorder (ΔS° > 0) even if the process is endothermic (ΔH° > 0). Example: Dissolution of NaCl.
Enthalpy-Driven Reactions
Reactions that are spontaneous due to exothermic heat release (ΔH° < 0) despite a decrease in disorder (ΔS° < 0).
Final Thoughts
Gibbs Free Energy provides a powerful tool to predict whether a reaction is thermodynamically favorable. Understanding how enthalpy, entropy, and temperature interact allows chemists to forecast reaction behavior and design processes with desired outcomes.
Recent Comments


9.10 Electrolysis and Faraday's Law


9.9 Cell Potential Under Nonstandard Conditions


9.8 Cell Potential and Free Energy


9.7 Galvanic (Voltaic) and Electrolytic Cells


5.2 Representations of Changes in Momentum

