3.5 Kinetic Molecular Theory

The Kinetic Molecular Theory (KMT)

Ideal Gases Ideal gases are theoretical gases that behave perfectly under all conditions, following the ideal gas law (PV = nRT) precisely. In real life, gases like H₂ and He behave most like ideal gases because they are small, non-polar particles. The conditions that favor ideal gas behavior are low pressure and high temperature—referred to by the acronym PLIGHT (Pressure Low, Ideal Gas, High Temperature).

Kinetic Energy (KE)

As you’ve learned before, temperature is directly related to the average kinetic energy of gas particles. As temperature increases, gas particles move faster. The formula for the kinetic energy of a gas particle is:

$$KE = \frac{1}{2}mv^2$$

Where:

• $KE$ = kinetic energy (measured in joules)
• $m$ = mass of the molecule (in kg)
• $v$ = speed of the molecule (in m/s)

This formula is given on the AP Chemistry reference sheet, and while you don’t have to memorize it, understanding it is crucial for explaining the behavior of gas particles. Remember that all particles are in constant random motion, and their speed depends on temperature.

The Five Assumptions of KMT

The Kinetic Molecular Theory relies on the following five main assumptions:

1. There are no attractive or repulsive forces between gas particles.
2. Gas particles are separated by great distances compared to their size—gas particles have negligible volume.
3. Gas particles move in random, constant, straight-line motion.
4. Collisions are elastic—when gas particles collide, they transfer energy without a net loss.
5. The kinetic energy of particles is directly related to their velocity ($KE = \frac{1}{2}mv^2$). All gases have the same average kinetic energy at a given temperature.
   
   

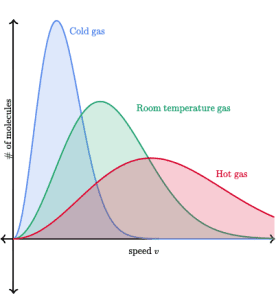
Maxwell-Boltzmann Distributions

The Maxwell-Boltzmann distribution shows the range of velocities (or energies) that gas particles possess at a specific temperature.

• Key point: A high peak on a Boltzmann distribution does not indicate that particles have more energy; rather, it means that more particles have that specific energy.

Here’s what you need to remember:

• As temperature increases, the range of velocities increases, and particles move at higher speeds.
• The distribution flattens as temperature increases, showing more molecules moving at higher speeds.
  

AP Free-Response Example (2019 #4)

A student experiments with CO₂(g) in a rigid container, initially at 299 K and 0.70 atm. The temperature of the gas is then increased to 425 K.

Part 1: Describe the effect of raising the temperature on the motion of the CO₂(g) molecules.

• As the temperature increases, the average kinetic energy of the CO₂(g) molecules increases, causing the molecules to move faster.

Part 2: Calculate the pressure of the CO₂(g) in the container at 425 K.

• Since volume is constant (rigid container), you can use Gay-Lussac’s Law:

$$\frac{P_1}{T_1} = \frac{P_2}{T_2}$$

• Substitute known values:

$$\frac{0.70 \, \text{atm}}{299 \, \text{K}} = \frac{P_2}{425 \, \text{K}}$$

• Solve for $P_2$:

$$P_2 = 0.99 \, \text{atm}$$

Part 3: Explain why the pressure of CO₂(g) changes as it is heated to 425 K, based on KMT.

• As temperature increases, the CO₂ molecules move faster and collide with the walls of the container more frequently and forcefully, resulting in an increase in pressure.

Key Concepts to Remember:

• Temperature increases → Kinetic energy increases → Particle speed increases.
• Maxwell-Boltzmann distributions: Show the range of velocities, flattening at higher temperatures.
• Gay-Lussac’s Law: Describes the direct relationship between pressure and temperature when volume is constant.

Use these concepts to understand the behavior of gases in various conditions and how they relate to the Kinetic Molecular Theory.