

Table of Contents
ToggleUnderstanding Moles and Molar Mass in Chemistry
Moles and molar mass are fundamental concepts that allow us to quantify and interpret chemical substances effectively. Imagine trying to count individual atoms during a chemical reaction—it would be impossible! That’s where these concepts step in. Let’s dive into how scientists handle and measure these invisible building blocks.
The Atom
Before we get into moles, let’s quickly understand atoms, the basic units that make up every element. Atoms are incredibly tiny—so small that we cannot see them with the naked eye! Each atom is composed of three types of subatomic particles: protons, neutrons, and electrons.
Protons and neutrons are located in the nucleus, a small, dense core at the center of the atom. The nucleus is positively charged due to the positive charge of protons, while neutrons are neutral.
Electrons orbit around the nucleus and carry a negative charge, effectively counteracting the positive charge in the nucleus.
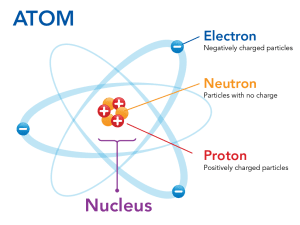
Understanding how atoms are structured helps us grasp why counting them is so challenging—they are just too small to quantify individually! Instead, chemists use a much larger, convenient unit called the mole.
What is a Mole?
Since it’s impossible to count individual atoms, chemists needed a practical way to correlate the mass of a substance to the number of particles involved in chemical reactions. That solution is the mole!
A mole is a unit that relates the mass of an element or compound to the number of particles (atoms, molecules, etc.) it contains. Think of it like a dozen: just as a dozen equals 12 items, a mole represents 6.022 × 10^23 particles (this is known as Avogadro’s number).
For example, a mole of carbon atoms contains 6.022 × 10^23 atoms, which makes it feasible to work with masses rather than individual atoms when doing chemical reactions.
Molar Mass
Molar mass is the mass (in grams) of one mole of a substance. It allows us to easily convert between mass, moles, and the number of particles. The units for molar mass are grams per mole (g/mol).
To find the molar mass of an element or compound, simply use the periodic table to determine the atomic masses of each element involved.
Example: To find the molar mass of water (H₂O):
Hydrogen (H): 1.008 g/mol, and there are 2 atoms of hydrogen in water.
Oxygen (O): 16.00 g/mol, and there is 1 atom of oxygen.
Calculation: (1.008 × 2) + 16.00 = 18.02 g/mol.
Thus, the molar mass of water is 18.02 g/mol.
Calculating Molar Mass for Compounds Let’s calculate the molar mass of another compound, carbon dioxide (CO₂).
Carbon (C) has an atomic mass of 12.01 g/mol.
Oxygen (O) has an atomic mass of 16.00 g/mol, and there are 2 atoms in CO₂.
Calculation: (12.01 × 1) + (16.00 × 2) = 44.01 g/mol.
So, the molar mass of carbon dioxide is 44.01 g/mol.
Avogadro’s Number
Think of Avogadro’s number as a chemistry version of a dozen, but instead of 12, it’s 6.022 × 10^23. A mole contains this many particles. For context, a mole of hockey pucks would have the same mass as the Moon!
This number is crucial when converting between grams, moles, and atoms during calculations in chemistry.
Dimensional Analysis: A Useful Tool
One of the most important skills in chemistry is dimensional analysis, which helps convert between units of measurement. This method is especially handy for converting grams to moles or moles to atoms.
Example: Converting Grams of CO₂ to Moles
Let’s say we have 50.0 grams of CO₂ and want to convert this to moles:
Start with the given value: 50.0 grams of CO₂.
Use the molar mass as a conversion factor (molar mass of CO₂ = 44.01 g/mol).
Set up the calculation:
➤ 50.0 grams CO₂ × (1 mole CO₂ / 44.01 grams CO₂) = 1.14 moles CO₂
Converting Moles to Atoms
Now let’s convert 1.14 moles of CO₂ to atoms:
Use Avogadro’s number:
➤ 1.14 moles CO₂ × (6.022 × 10^23 atoms / 1 mole CO₂) = 6.87 × 10^23 atoms of CO₂.
Finding the Number of Atoms of Each Element
Carbon Atoms: Since each molecule of CO₂ contains 1 atom of carbon, the number of carbon atoms in our 1.14 moles of CO₂ is 6.87 × 10^23.
Oxygen Atoms: Since each molecule of CO₂ contains 2 atoms of oxygen, the number of oxygen atoms is 2 × 6.87 × 10^23 = 1.37 × 10^24.
Practice Makes Perfect!
These types of calculations are key to success in chemistry, and understanding moles and molar mass will help you tackle more advanced topics. Don’t worry if it seems tricky at first—with practice, dimensional analysis and mole calculations will feel like second nature. Keep practicing, and soon these skills will be a piece of cake!

Avogadro’s Number: Understanding the Mole
Imagine the convenience of buying a dozen eggs. It’s a simple unit that tells you exactly how many eggs you get: twelve. In chemistry, a similar concept exists called the mole. Just like a dozen equals 12 eggs, one mole of any substance contains particles—whether those particles are atoms, molecules, or ions. This number, known as Avogadro’s number, helps scientists bridge the gap between the microscopic world of atoms and the macroscopic quantities we can measure in the lab.
To give you a sense of just how large Avogadro’s number is: if you had a mole of hockey pucks, it would weigh as much as the Moon! In practical terms, this large number helps us convert between grams, moles, and atoms, making it possible to understand chemical reactions at a tangible level.
Dimensional Analysis: The Secret Weapon for Chemistry Calculations
Dimensional analysis is one of the most fundamental tools in chemistry. Think of it as your secret weapon for converting between units. You’ve probably used dimensional analysis before without even realizing it! Whether it’s converting miles per hour to meters per second or inches to centimeters, dimensional analysis allows us to move between different units seamlessly.
Dimensional analysis is especially helpful when you’re stuck on a problem and can’t remember the exact formula. It helps you find the answer by converting what you already know into the unit you need. Here’s how you do it:
Identify the units you have and the units you need to convert to.
Write down the conversion factor that links these units.
Multiply by the conversion factor, ensuring your units cancel appropriately.
A conversion factor is simply a ratio that relates equivalent units—like 1 foot equals 12 inches, or 1 mole equals particles.
Dimensional Analysis with Moles and Molar Mass
Now that we’ve reviewed the basics of moles and molar mass, let’s practice using dimensional analysis to convert a sample of carbon dioxide (). Imagine we have 50.0 grams of and want to convert this into moles.
CO₂: Converting Grams to Moles
To convert grams to moles, we need a conversion factor involving molar mass. Here’s how it works:
Start with the number given in the problem: 50.0 grams of .
The molar mass of is calculated by adding the molar masses of carbon (12.01 g/mol) and oxygen (16.00 g/mol × 2 = 32.00 g/mol), giving us a total molar mass of 44.01 g/mol.
Use the conversion factor:
Notice that grams cancel out, leaving us with moles—the desired unit. It’s helpful to remember that moles can be calculated as:
CO₂: Converting Moles to Atoms
Now, let’s convert 1.14 moles of into atoms using Avogadro’s number.
Start with what you have: 1.14 moles of .
Multiply by Avogadro’s number to convert moles to particles:
By multiplying, we cancel out moles, and we’re left with atoms. Avogadro’s number always serves as the conversion factor when going from moles to atoms or molecules.
CO₂: Finding the Number of Atoms of C and O
But what if we want to know how many individual atoms of carbon and oxygen there are in our sample?
Carbon: Since the subscript on carbon in is 1, the number of carbon atoms is equivalent to the number of molecules. Thus, we have carbon atoms.
Oxygen: For oxygen, the subscript is 2, which means each molecule has 2 oxygen atoms. Therefore, we need to multiply by 2:
Practice Makes Perfect
Dimensional analysis may seem tricky at first, but once you practice a few problems, it becomes second nature. It’s like a puzzle—you just need to find the right pieces to connect the units you have to the units you need. And remember, while problems may become more complex as you progress, the fundamentals of dimensional analysis always remain the same. Keep practicing, and soon it’ll be a piece of cake!
Recent Comments


1.8 Valence Electrons and Ionic Compounds


1.5 Atomic Structure and Electron Configuration


Discover the Ultimate Multiplication Tables Generator – A Comprehensive Guide


Basic Algebra Concepts: Lesson 2.2


Basic Algebra Concepts: Lesson 1.4

