1.6 Conservation of Energy in Fluid Flow
Introduction
The principle of conservation of energy applies seamlessly to fluid flow, much like it does to solids. However, with fluids, we account for density and volume instead of just mass. This leads to the derivation of Bernoulli’s equation, which serves as a cornerstone for understanding energy dynamics in fluid systems.
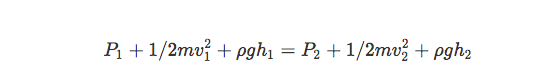
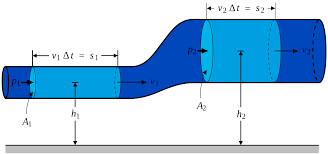
Bernoulli’s Equation
Bernoulli’s equation is derived from the conservation of energy principle, making specific assumptions:
The fluid is incompressible.
The flow is steady and streamlined.
Turbulence and viscosity are negligible.
Formula:
Where:
: Pressure (Pa)
: Density of the fluid (kg/m³)
: Velocity of the fluid (m/s)
: Acceleration due to gravity (m/s²)
: Height above a reference point (m)
Example Problem
Problem: Water flows at a rate of 2 m³/s through a tube with a diameter of 1 m and an initial pressure of 80 kPa. What is the pressure after the tube narrows to a diameter of 0.5 m?
Solution:
Step 1: Continuity Equation
Calculate the cross-sectional areas:
Calculate the velocities:
Step 2: Bernoulli’s Equation Remove terms for height since it doesn’t change:
Substituting values:
Simplify:
Special Case: Leaking Tank
In a leaking tank, water at the top has potential and kinetic energy. The flow rate, defined as , remains constant for both the top and the leak point. Since the top has a much larger area, its velocity is negligible, simplifying calculations.

Key Points About Energy Conservation in Fluids
Kinetic Energy (KE): Energy due to motion:
Potential Energy (PE): Energy due to position:
Total Energy: Sum of KE and PE, remaining constant in a closed system.
Flow Dynamics: The energy transfer between kinetic and potential energy is dictated by Bernoulli’s equation.
Example Problem
Problem: A pump lifts water from a depth of 2 m to a height of 10 m at 5 kW power. How much work is done?
Step 1: Potential Energy Change
Substitute values:
Step 2: Work Done by Pump
Rearrange for time:
Calculate:
Work done:
Conservation of energy in fluid flow unifies key physics concepts, offering insights into fluid behavior in real-world systems. Mastery of Bernoulli’s equation and related principles opens doors to understanding engineering and natural phenomena.







