3.1 Vector Fields: An In-Depth Look at Circular Motion

Learning Targets

A vector field gives the value of a physical quantity that is described by a vector as a function of position (and sometimes time).

What is a Vector Field?

A vector field assigns a vector to each point in a portion of space. These vectors, represented as arrows, indicate the magnitude and direction of a physical quantity.

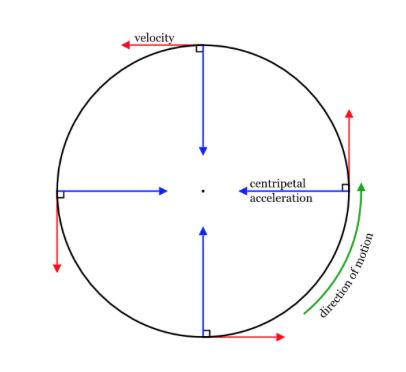
For example, the vector field in circular motion represents the tangential velocity of an object moving in a circle. Each vector is tangent to the circle, touching it at only one point, and has a constant magnitude but a changing direction.

Uniform Circular Motion (UCM)

Key Concept: Uniform circular motion refers to the motion of an object in a circle at constant speed but changing direction, resulting in constant acceleration.

UCM in Action

Imagine a car making a turn at a constant speed. Although its speed doesn’t change, its direction does, meaning the car is accelerating. This acceleration is caused by forces like tension, friction, gravity, or normal force, which contribute to centripetal force—the center-seeking force that causes circular motion.

Centripetal vs. Centrifugal Forces

• Centripetal Force: A real force directed toward the center of the circle, causing acceleration.
  Equation:

  $$F_c = \frac{{mv^2}}{r}$$

  Where $F_c$ is the centripetal force (N), $m$ is mass (kg), $v$ is velocity (m/s), and $r$ is the radius (m).

• Centrifugal Force: A perceived force in a rotating frame, often misunderstood as a real force. It results from inertia, creating the sensation of being pushed outward.

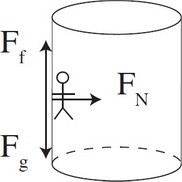
Misconception Alert: Centrifugal Force

The centrifugal force is not an actual force; it’s the result of an object’s inertia. For example, in an amusement park ride that spins, it feels like you’re being pushed against the wall. In reality:

• The force of static friction keeps you from sliding down.
• The faster the spin, the greater the static friction, which counteracts gravity and pins you to the wall.

Free-Body Diagrams in UCM

In UCM, forces pointing toward the center are positive (+), and those pointing away from the center are negative (-). Forces not directed toward or away from the center aren’t included in the net force.

Key Considerations

• Velocity is tangent to the circle and isn’t part of the net force calculation.
• Centripetal force is the net force, not a separate force, and shouldn’t appear in free-body diagrams.

Vector Fields and Gravitational Forces

A simplified vector field can represent gravitational attraction between two objects, such as Earth and the Moon.

How It Works

• A vector field uses arrows to represent the gravitational pull between objects.
• Example: The Earth’s gravitational force pulls the Moon toward it, while the Moon exerts a weaker pull on the Earth.
• Calculations are simplified using the distance between their centers of mass.

Key Equations

For two objects interacting gravitationally:

$$F = G \frac{{m_1 \cdot m_2}}{{r^2}}$$

Where:

• $F$ is the gravitational force (N).
• $m_1$ and $m_2$ are the masses (kg).
• $r$ is the distance between the centers of mass (m).
• $G$ is the gravitational constant ($6.674 \times 10^{-11} \, \text{N·m}^2/\text{kg}^2$)